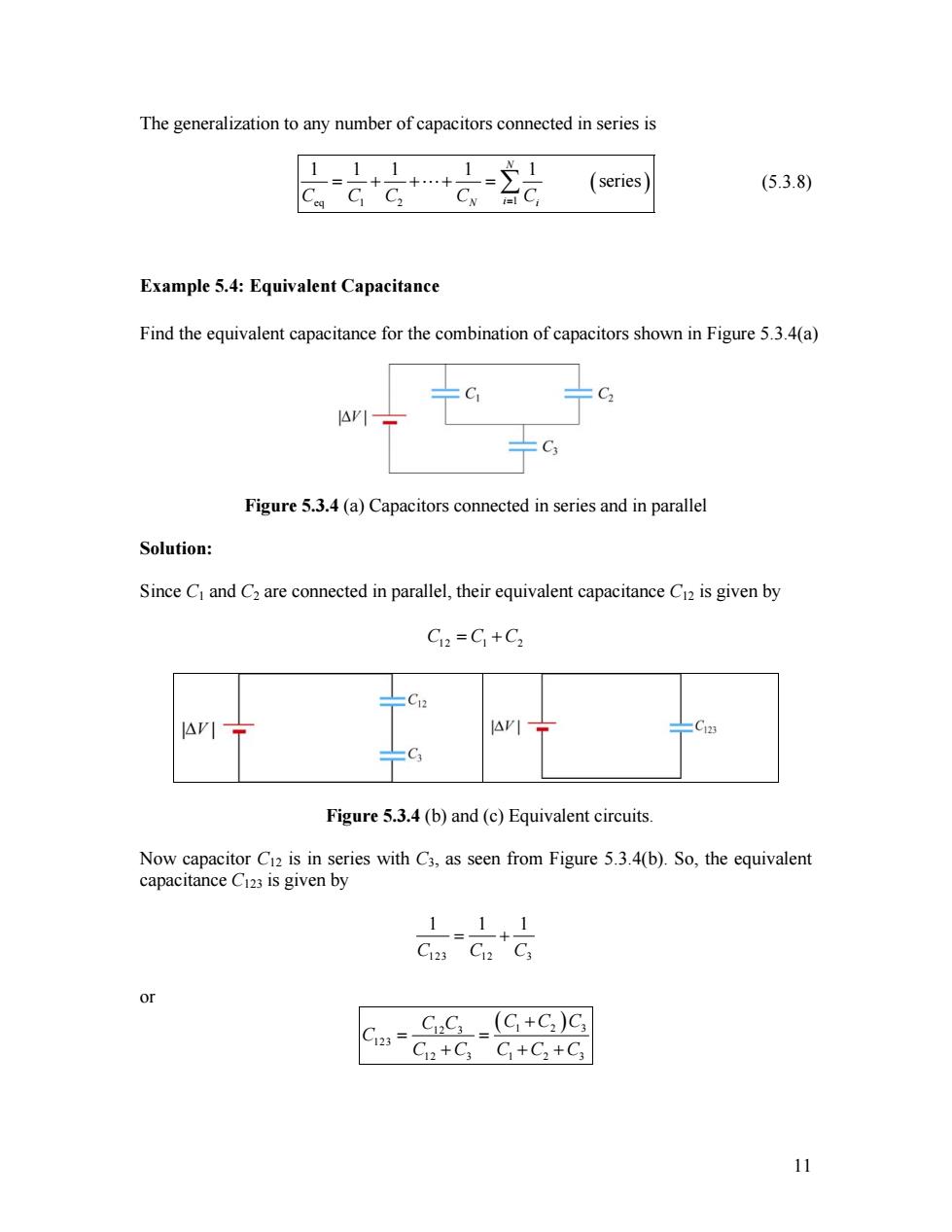
The generalization to any number of capacitors connected in series is 11 1 十十 1=1 (series (5.3.8) Example 5.4:Equivalent Capacitance Find the equivalent capacitance for the combination of capacitors shown in Figure 5.3.4(a) Figure 5.3.4 (a)Capacitors connected in series and in parallel Solution: Since C and C2 are connected in parallel,their equivalent capacitance C12 is given by CI2=C]+C2 lrI C23 =C3 Figure 5.3.4(b)and (c)Equivalent circuits Now capacitor C12 is in series with C3,as seen from Figure 5.3.4(b).So,the equivalent capacitance C123 is given by 111 C123 C12 C3 or Ci2C:_(C+C2)C; C2+C3C1+C2+C3 11The generalization to any number of capacitors connected in series is ( eq 1 2 1 1 1 1 1 1 series N C C C CN i i= C = + +"+ = ∑ ) (5.3.8) Example 5.4: Equivalent Capacitance Find the equivalent capacitance for the combination of capacitors shown in Figure 5.3.4(a) Figure 5.3.4 (a) Capacitors connected in series and in parallel Solution: Since C1 and C2 are connected in parallel, their equivalent capacitance C12 is given by C C 12 = 1 +C2 Figure 5.3.4 (b) and (c) Equivalent circuits. Now capacitor C12 is in series with C3, as seen from Figure 5.3.4(b). So, the equivalent capacitance C123 is given by 123 12 3 1 1 C C C = + 1 or ( 1 2 ) 12 3 123 12 3 1 2 3 C C C C C C C C C C C + = = + + + 3 11