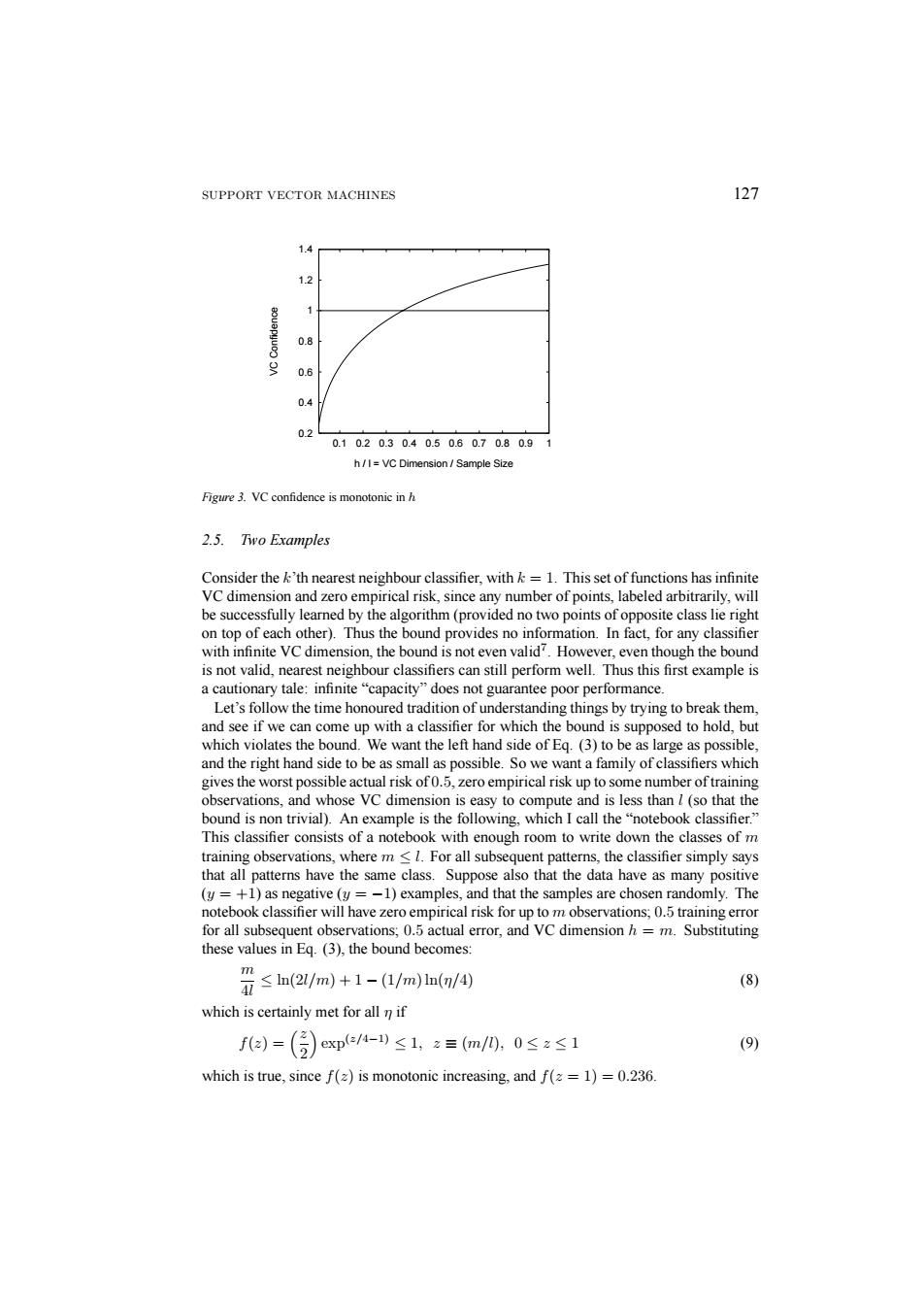
SUPPORT VECTOR MACHINES 127 1.4 1.2 0.8 9 0.6 0.4 02 0.1020.30.40.50.60.70.80.91 h/I=VC Dimension Sample Size Figure 3.VC confidence is monotonic in h 2.5.Two Examples Consider the k'th nearest neighbour classifier.with k=1.This set of functions has infinite VC dimension and zero empirical risk,since any number of points,labeled arbitrarily,will be successfully learned by the algorithm(provided no two points of opposite class lie right on top of each other).Thus the bound provides no information.In fact,for any classifier with infinite VC dimension,the bound is not even valid?.However,even though the bound is not valid,nearest neighbour classifiers can still perform well.Thus this first example is a cautionary tale:infinite"capacity"does not guarantee poor performance. Let's follow the time honoured tradition of understanding things by trying to break them, and see if we can come up with a classifier for which the bound is supposed to hold,but which violates the bound.We want the left hand side of Eq.(3)to be as large as possible, and the right hand side to be as small as possible.So we want a family of classifiers which gives the worst possible actual risk of0.5,zero empirical risk up to some number of training observations,and whose VC dimension is easy to compute and is less than l(so that the bound is non trivial).An example is the following,which I call the"notebook classifier." This classifier consists of a notebook with enough room to write down the classes of m training observations,where m<1.For all subsequent patterns,the classifier simply says that all patterns have the same class.Suppose also that the data have as many positive (y=+1)as negative (y=-1)examples,and that the samples are chosen randomly.The notebook classifier will have zero empirical risk for up to m observations;0.5 training error for all subsequent observations;0.5 actual error,and VC dimension h=m.Substituting these values in Eq.(3),the bound becomes: ≤n(2/m）+1-(1/m)ln(/④ m (8) which is certainly met for all n if fa=()exp-)≤1，z=m/0,0≤z≤1 (9) which is true,since f(z)is monotonic increasing,and f(=1)=0.236.SUPPORT VECTOR MACHINES 127 0.2 0.4 0.6 0.8 1 1.2 1.4 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 VC Confidence h / l = VC Dimension / Sample Size Figure 3. VC confidence is monotonic in h 2.5. Two Examples Consider the k’th nearest neighbour classifier, with k = 1. This set of functions has infinite VC dimension and zero empirical risk, since any number of points, labeled arbitrarily, will be successfully learned by the algorithm (provided no two points of opposite class lie right on top of each other). Thus the bound provides no information. In fact, for any classifier with infinite VC dimension, the bound is not even valid7. However, even though the bound is not valid, nearest neighbour classifiers can still perform well. Thus this first example is a cautionary tale: infinite “capacity” does not guarantee poor performance. Let’s follow the time honoured tradition of understanding things by trying to break them, and see if we can come up with a classifier for which the bound is supposed to hold, but which violates the bound. We want the left hand side of Eq. (3) to be as large as possible, and the right hand side to be as small as possible. So we want a family of classifiers which gives the worst possible actual risk of 0.5, zero empirical risk up to some number of training observations, and whose VC dimension is easy to compute and is less than l (so that the bound is non trivial). An example is the following, which I call the “notebook classifier.” This classifier consists of a notebook with enough room to write down the classes of m training observations, where m ≤ l. For all subsequent patterns, the classifier simply says that all patterns have the same class. Suppose also that the data have as many positive (y = +1) as negative (y = −1) examples, and that the samples are chosen randomly. The notebook classifier will have zero empirical risk for up to m observations; 0.5 training error for all subsequent observations; 0.5 actual error, and VC dimension h = m. Substituting these values in Eq. (3), the bound becomes: m 4l ≤ ln(2l/m)+1 − (1/m) ln(η/4) (8) which is certainly met for all η if f(z) = ³z 2 ´ exp(z/4−1) ≤ 1, z ≡ (m/l), 0 ≤ z ≤ 1 (9) which is true, since f(z) is monotonic increasing, and f(z = 1) = 0.236