
Digital Signal Processing 主讲:张君 上文大兽
Digital Signal Processing 主讲:张君

FFT-Introduce Digital Signal Processing--DFT/FFT Algorithms DFT plays an important role in the analysis,design,and implementation of discrete-time signal-processing algorithms and systems.Because direct computing DFT needs N2 complex multiplication,when N is larger, computation cost is larger.Before FFT comes,it is not practical that using DFT spectrum analysis and real-time processing of signal.Until in 1965 fast computation algorithm turn up,situation didn't change (J.W.Cooley,J. W.Tukey,G.Sande). 上浒充通大
Digital Signal Processing—— DFT/FFT Algorithms FFT- Introduce DFT plays an important role in the analysis, design, and implementation of discrete-time signal-processing algorithms and systems. Because direct computing DFT needs N2 complex multiplication , when N is larger, computation cost is larger. Before FFT comes,it is not practical that using DFT spectrum analysis and real-time processing of signal 。 Until in 1965 fast computation algorithm turn up,situation didn’t change (J. W. Coo1ey, J. W. Tukey, G. Sande)

FFT Digital Signal Processing--DFT/FFT Algorithms The discrete Fourier transform plays an important role in many applications of digital signal processing,including linear filtering,correlation analysis,and spectrum analysis.The major reason is the existence of efficient algorithms for computing the DFT. A divide-and-conquer approach in which a DFT of size N,where N is a composite number,is reduced to the computation of smaller DFTs from which the larger DFT is computed.Particularly for N=2B. A linear filtering operation on the data,this approach has two algorithms:the Goertzeland the chirp-z transform algorithms. 上游充通大
Digital Signal Processing—— DFT/FFT Algorithms FFT The discrete Fourier transform plays an important role in many applications of digital signal processing, including linear filtering, correlation analysis, and spectrum analysis. The major reason is the existence of efficient algorithms for computing the DFT. A divide-and-conquer approach in which a DFT of size N, where N is a composite number, is reduced to the computation of smaller DFTs from which the larger DFT is computed. Particularly for N=2B. A linear filtering operation on the data, this approach has two algorithms: the Goertzeland the chirp-z transform algorithms

DFT (Direct Compute) Digital Signal Processing--DFT/FFT Algorithms Complex Complex Real Real Multiplication Addition Multiplication Addition Y- X()∑xn)wN N-1 4N 2N+2(W-1) N X(k) N2 W(W-1) 4W2 2W(2W-1) 上游充通大
Digital Signal Processing—— DFT/FFT Algorithms DFT (Direct Compute) X k( ) 1 0 ( ) N nk N n x n W N N 1 4N 2 2( 1) N N N X k( ) 2 N N N( 1) 2 4N 2 (2 1) N N Complex Multiplication Complex Addition Real Multiplication Real Addition

Improve of DFT Digital Signal Processing--DFT/FFT Algorithms Symmetry (Wt)=W Periodicity Wik-WNim)k -WaNk) WWINW W W=1 W2=-1 WW+N/2)=-W DIT:Decimation-In-Time DIF:Decimation-In-Frequency 上游充通大¥
Digital Signal Processing—— DFT/FFT Algorithms Improve of DFT * nk nk W W N N nk N n k n N k ( ) ( ) W W W N N N nk mnk W W N mN / / nk nk m W W N N m 0 1 WN / 2 1 N WN ( /2) k N k W W N N Periodicity Symmetry DIT: Decimation-In-Time DIF: Decimation-In-Frequency

Basic principle of DIT-FFT Digital Signal Processing--DFT/FFT Algorithms FFT Algorithm has 2 types Decimation In Time FFT,(DIT-FFT) and Decimation In Frequency FFT(DIF-FFT)。First DIF-FFT。 Length of x(n)is N,and N=2M,M∈N Depended on odd-even of n,x(n)is divided into two N/2-point sub-sequence N x(r)=x(2r), r=0,1,.-1 2 x2(r)=x(2r+1),r=0,1,. 上游交通大学
Digital Signal Processing—— DFT/FFT Algorithms Basic principle of DIT-FFT FFT Algorithm has 2 types : Decimation In Time FFT,(DIT-FFT) and Decimation In Frequency FFT(DIF―FFT)。First DIF―FFT。 Length of x(n) is N,and Depended on odd-even of n, x(n) is divided into two N/2-point sub-sequence 2 , M N M ∈N 1 2 ( ) (2 ), 0,1, 1 2 ( ) (2 1), 0,1, 1 2 N x r x r r N x r x r r

DIT-FFT Digital Signal Processing--DFT/FFT Algorithms DFT[X(n)]=X(k)=∑x(n)W+∑x(n)W n= N72 W/2-1 ∑x(2r)w+∑x(2r+1)w2+ r= =0 N/2-1 N/2-1 (rW2+m∑x(r)W r=0 三0 2π JN W 22k 二e JN =e 2 =W2 N/2-1 N/2-1 .X(k)=∑ x(rW+Wx(rW2=X(k)+WX(k) r=0 上游充通大¥
Digital Signal Processing—— DFT/FFT Algorithms DIT-FFT DFT [x(n)]= /2 1 /2 1 2 (2 1) 0 0 /2 1 /2 1 2 2 1 2 0 0 ( ) ( ) ( ) (2 ) (2 1) ( ) ( ) kn kn N N n n N N kr k r N N r r N N kr k kr N N N r r X k x n W x n W x r W x r W x r W W x r W ∵ 2 2 2 2 2 / 2 j kr N j kr kr kr N W e e W N N ∴ / 2 1 / 2 1 1 / 2 2 / 2 1 2 0 0 ( ) ( ) ( ) ( ) ( ) N N kr k kr k N N N N r r X k x r W W x r W X k W X k

DIT-FFT Digital Signal Processing--DFT/FFT Algorithms X1(k)=DFT[x1(r)]X2(k)=DFT[x2(r)]N/2Points, That is N/2-1 X (k)=>x(r)WN2=DFT[x(r)] r=0 /2-1 X,()=∑ x2(r)WNn2=DFT[x2(r)] r=0 X(k)、X,k)(N/2),And m宁=-n,∴Xk) X(k)=X(k)+WX2()k=0,1,. Xk+当=x-WX,)k=0,1 2 上游充通大粤
Digital Signal Processing—— DFT/FFT Algorithms DIT-FFT X1(k)=DFT[x1(r)]、X2(k)=DFT[ x2(r)] N/2Points, That is / 2 1 1 1 / 2 1 0 / 2 1 2 2 / 2 2 0 ( ) ( ) [ ( )] ( ) ( ) [ ( )] N kr N r N kr N r X k x r W DFT x r X k x r W DFT x r X1 (k)、X2 (k) (N/2),And ,∴X(k) 2 N k k W W N N 1 2 1 2 ( ) ( ) ( ) 0,1, 1 2 ( ) ( ) ( ) 0,1, 1 2 2 k N k N N X k X k W X k k N N X k X k W X k k

DIT-FFT Digital Signal Processing--DFT/FFT Algorithms A A十BC B ·A-BC Fig Butterfly computation 上游充通大学
Digital Signal Processing—— DFT/FFT Algorithms DIT-FFT C A B A+ B C A- B C Fig Butterfly computation
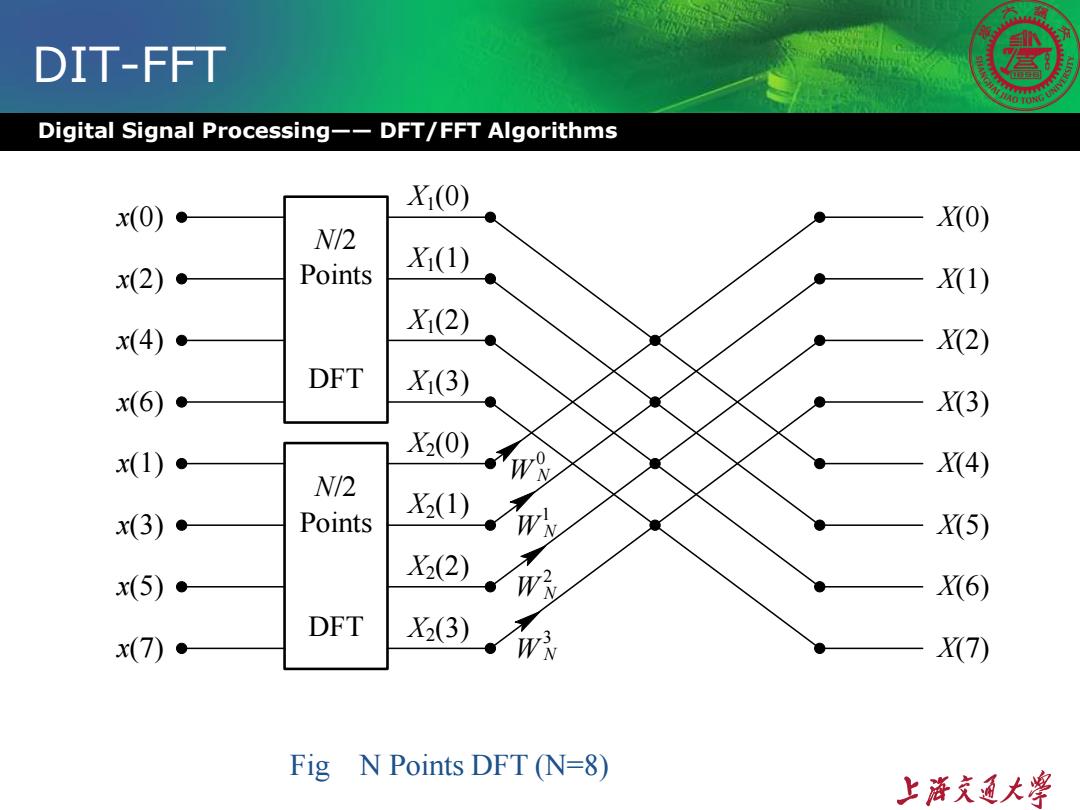
DIT-FFT Digital Signal Processing--DFT/FFT Algorithms X(0) x(0) ● X(0) N/2 Points X1(1) x(2) X1) X1(2) x(4) X2) DFT X(3) x(6) X3) X2(0) x(1) X4) N/2 X2(1) x(3) Points X5) X2(2) x(5) W呢 X6) DFT X2(3) x(7) P究 X7) Fig N Points DFT(N=8) 上游充通大¥
Digital Signal Processing—— DFT/FFT Algorithms DIT-FFT Fig N Points DFT (N=8) N/2 Points DFT W N 0 N/2 Points DFT W N 1 W N 2 W N 3 x(0) X1(0) x(2) x(4) x(6) x(1) x(3) x(5) x(7) X1(1) X1(2) X1(3) X2(0) X2(1) X2(2) X2(3) X(0) X(1) X(2) X(3) X(4) X(5) X(6) X(7)