
数值计算
数值计算

数据类型 ·程序存储与操作的信息称为数据 ·数据分成不同类型:不同的存储与操作 ·为何要分类型? 一类型本身代表了某种信息,可为程序利用 人编译器/解释器利用类型检查,可以发现程序错误 一不同类型有不同实现效率,可选最合适类型. 数据的类型决定了数据能取什么值,以及 能做哪些运算(操作) Lu Chaojun,SJTU 2
数据类型 • 程序存储与操作的信息称为数据. • 数据分成不同类型:不同的存储与操作. • 为何要分类型? – 类型本身代表了某种信息,可为程序利用 ©编译器/解释器利用类型检查,可以发现程序错误. – 不同类型有不同实现效率,可选最合适类型. • 数据的类型决定了数据能取什么值,以及 能做哪些运算(操作). Lu Chaojun, SJTU 2

数值数据类型 。整数类型int 一不带小数点 -可存储整数的精确值 ·浮点数类型float -带小数点 一计算机只能存储浮点数的近似值: ·经验:如果不是确实需要小数,就用int. type()函数 -返回的值的类型 Lu Chaojun,SJTU 3
数值数据类型 • 整数类型int – 不带小数点 – 可存储整数的精确值 • 浮点数类型float – 带小数点 – 计算机只能存储浮点数的近似值! • 经验:如果不是确实需要小数,就用int. • type()函数 – 返回的值的类型 Lu Chaojun, SJTU 3
数值运算符 运算符 整数 浮点数 + 加 加 减 减 乘 乘 除(结果取整) 除 米米 乘方 乘方 % 余数 (商取整时的)余数 abs() 绝对值 绝对值 整数和浮点数可以混合运算: ·运算数都是整数,结果为整数; ·至少有一个运算数是浮点数,结果为浮点数. Lu Chaojun,SJTU
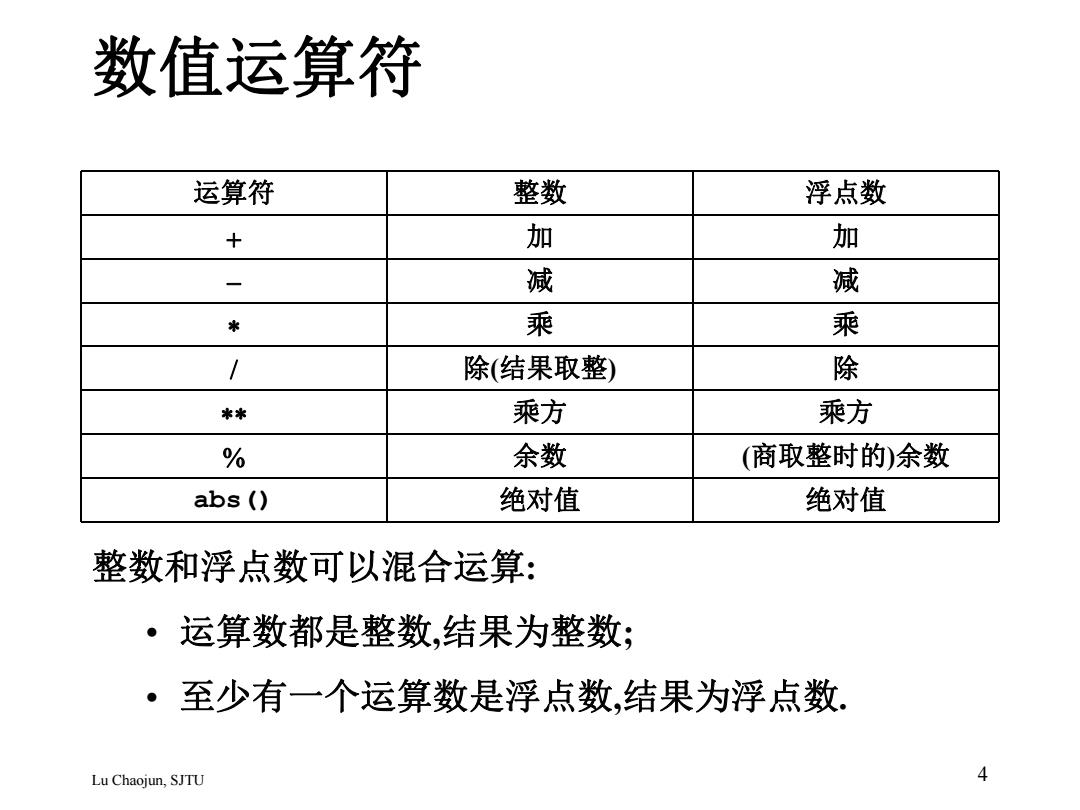
数值运算符 运算符 整数 浮点数 加 加 减 减 乘 乘 除(结果取整) 除 乘方 乘方 余数 (商取整时的)余数 abs() 绝对值 绝对值 Lu Chaojun, SJTU 4 整数和浮点数可以混合运算: • 运算数都是整数,结果为整数; • 至少有一个运算数是浮点数,结果为浮点数

数学库 ·库:包含有用定义的模块 一最常见的是函数定义 一一般由系统提供,也可自己开发给别人用 数学库:包含有用的数学函数 ·数学库的引入: import math 数学库中函数的调用:例如求平方根 math.sqrt (
数学库 • 库:包含有用定义的模块. – 最常见的是函数定义 – 一般由系统提供,也可自己开发给别人用. • 数学库:包含有用的数学函数. • 数学库的引入: import math • 数学库中函数的调用:例如求平方根 math.sqrt()

编程例:quadratic.py import math def main ( a,b,c input("Enter three coefficients:" discRoot math.sqrt(b*b -4*a*c) r1 (-b discRoot)/(2 a) r2 (-b discRoot)/(2 a) print WThe solutions are:"r1,r2 -用到math.sgrt()函数 -小测验:不用sqrt0能求平方根吗? 人库函数一般效率高 Lu Chaojun,SJTU 6
编程例:quadratic.py import math def main() a, b, c = input(“Enter three coefficients: ”) discRoot = math.sqrt(b*b – 4*a*c) r1 = (-b + discRoot) / (2 * a) r2 = (-b – discRoot) / (2 * a) print “The solutions are:” , r1, r2 – 用到math.sqrt()函数 – 小测验:不用sqrt()能求平方根吗? ©库函数一般效率高. Lu Chaojun, SJTU 6

数学库中的常用函数 pi:常数π e:常数e sqrt(x):平方根 sin(x),cos(x),tan(x),asin(x),acos(x),atan(x):三角函数 log(x),log10(x):自然对数与常用对数 exp(x):e的x次方 ceil(x):≥x的最小整数 floor(x):≤x的最大整数
数学库中的常用函数 pi : 常数 e : 常数e sqrt(x): 平方根 sin(x), cos(x), tan(x), asin(x), acos(x), atan(x): 三角函数 log(x), log10(x):自然对数与常用对数 exp(x): e的x次方 ceil(x): x的最小整数 floor(x): x的最大整数

一种常用算法模式:累积 ·最终结果是由逐个中间结果累积起来形成的. 一例如6:的计算:先算6*5,再*4,,再*1而得. 。 这种累积程序需要一个存放累积结果的变量,累 积过程是一个循环: 初始化累积变量 循环直至得到最终结果 计算累积变量的当前累积值 ·初始化:给累积变量一个合适的初值,以便进入 循环后能正确计算. 一忘记初始化是一个常见编程错误!
一种常用算法模式:累积 • 最终结果是由逐个中间结果累积起来形成的. – 例如6!的计算:先算6*5,再*4,…,再*1而得. • 这种累积程序需要一个存放累积结果的变量,累 积过程是一个循环: 初始化累积变量 循环直至得到最终结果 计算累积变量的当前累积值 • 初始化:给累积变量一个合适的初值,以便进入 循环后能正确计算. – 忘记初始化是一个常见编程错误!

例:阶乘计算程序 ·具体数(如6)的阶乘 fact 1 for f in[6,5,4,3,2,1]: fact fact f ·一般情形 n input (Enter a number:" fact =1 for f in range (n,1,-1): fact fact f print "The factorial of "n,"is",fact
例:阶乘计算程序 • 具体数(如6)的阶乘 fact = 1 for f in [6,5,4,3,2,1]: fact = fact * f • 一般情形 n = input(" Enter a number: ") fact = 1 for f in range(n,1,-1): fact = fact * f print "The factorial of " ,n, "is" ,fact

阶乘程序的几点注解 由于乘法结合律,累积的次序是不重要的 如按下面的循环来累积: for f in[2,3,4,5,6]: for f in[2,4,6,1,3,5]: for f in range(2,n+1) ·range()函数 range (n) range (start,n) range(start,n,step) ·fact也可初始化为n
阶乘程序的几点注解 • 由于乘法结合律,累积的次序是不重要的. 如按下面的循环来累积: for f in [2,3,4,5,6]: for f in [2,4,6,1,3,5]: for f in range(2,n+1) • range()函数 range(n) range(start,n) range(start,n,step) • fact也可初始化为n