
第6章树和二叉树 从对线性结构的研究过渡到对树形 结构的研究,是数据结构课程学习的一 次跃变
从对线性结构的研究过渡到对树形 结构的研究,是数据结构课程学习的一 次跃变

6.1 树的定义和基本术语 1.树的定义(非递归) 树是由n(n≥0)个结点组成的有限集合。 如果n=0,称为空树; 如果n>0,则: ·有一个特定的称之为根(roo)的结点,它只有 后继,但没有前驱; ·其余结点有且仅有一个直接前驱,但可以有0 个或多个后继
6.1 树的定义和基本术语 1. 树的定义 (非递归) 树是由n (n 0)个结点组成的有限集合。 如果n = 0,称为空树; 如果n > 0,则: ▪ 有一个特定的称之为根(root)的结点,它只有 后继,但没有前驱; ▪ 其余结点有且仅有一个直接前驱,但可以有0 个或多个后继

A B E F H 是不是一棵树?
是不是一棵树?

2、树的基本术语
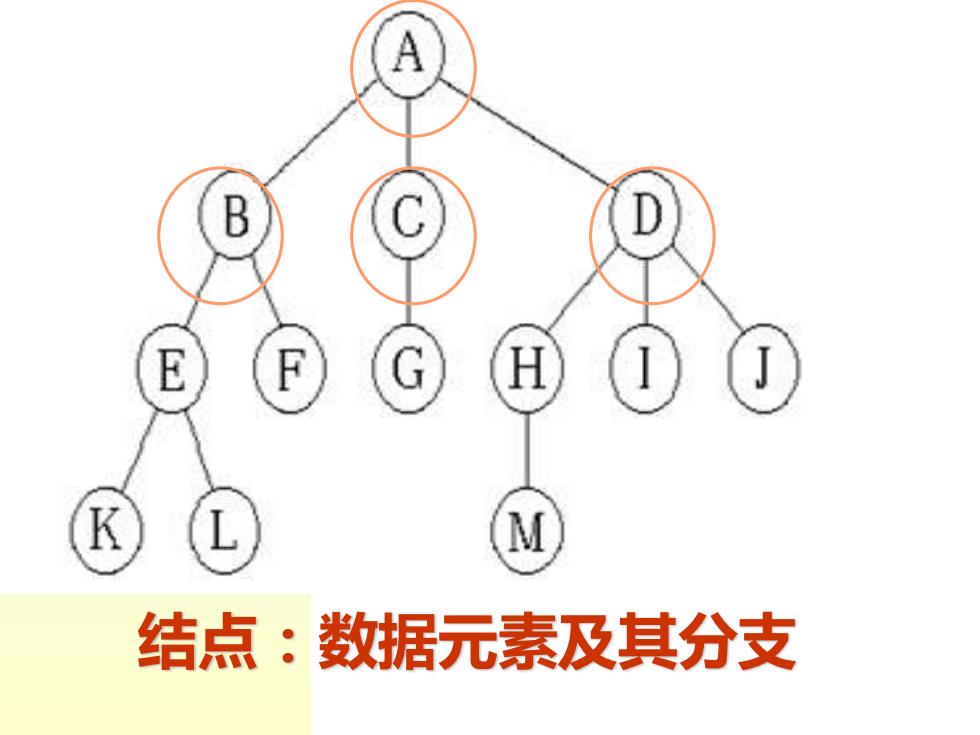
A B C E F H M 结点:数据元素及其分支
结点:数据元素及其分支
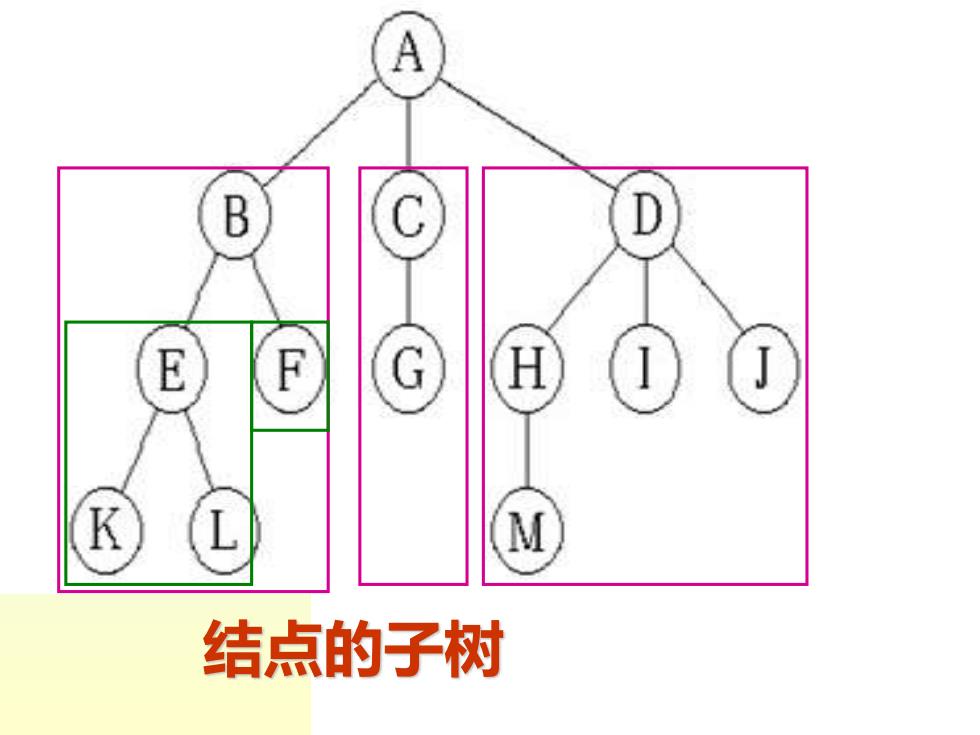
A B C D E E © H K L M 结点的子树
结点的子树
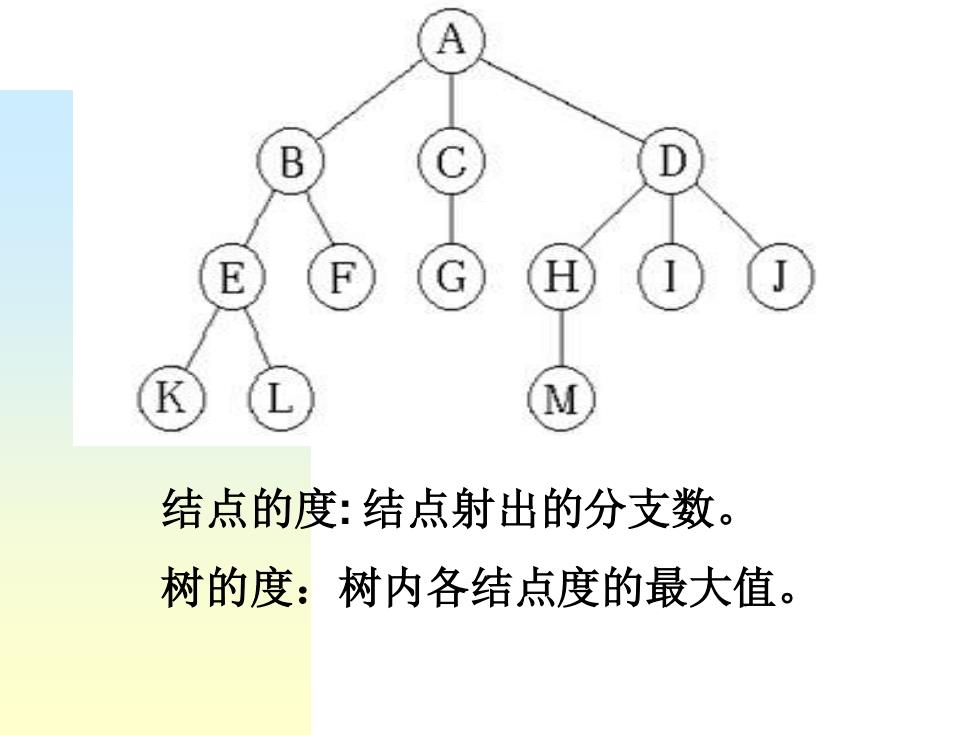
A B 结点的度:结点射出的分支数。 树的度:树内各结点度的最大值
结点的度: 结点射出的分支数。 树的度:树内各结点度的最大值
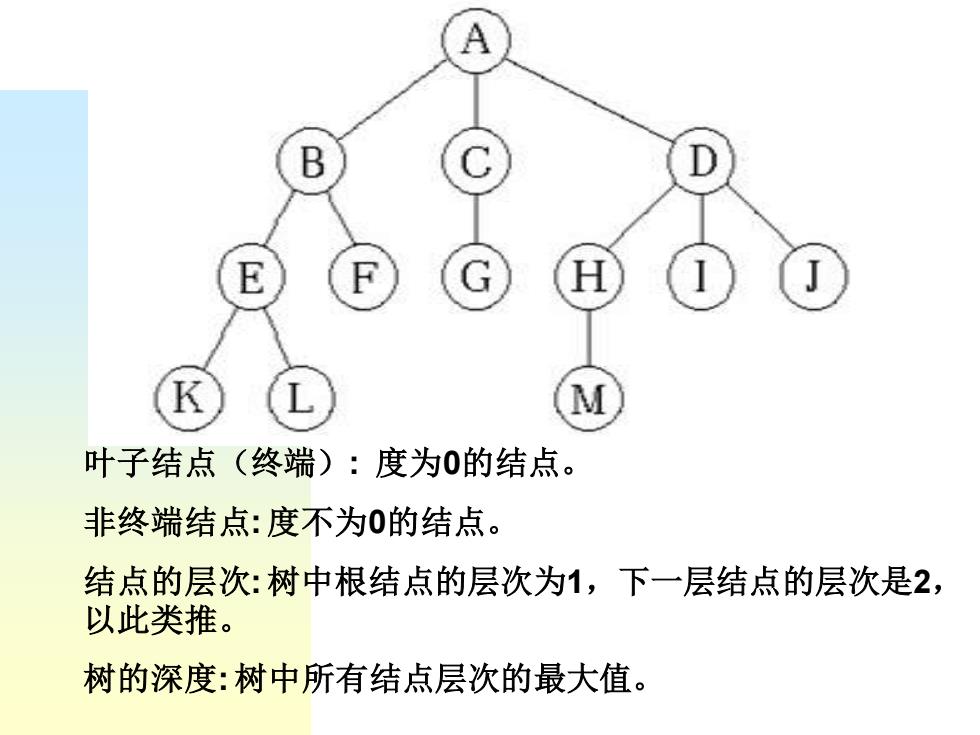
A B 叶子结点(终端):度为0的结点。 非终端结点:度不为0的结点。 结点的层次:树中根结点的层次为1,下一层结点的层次是2, 以此类推。 树的深度:树中所有结点层次的最大值
叶子结点(终端): 度为0的结点。 非终端结点: 度不为0的结点。 结点的层次: 树中根结点的层次为1,下一层结点的层次是2, 以此类推。 树的深度: 树中所有结点层次的最大值
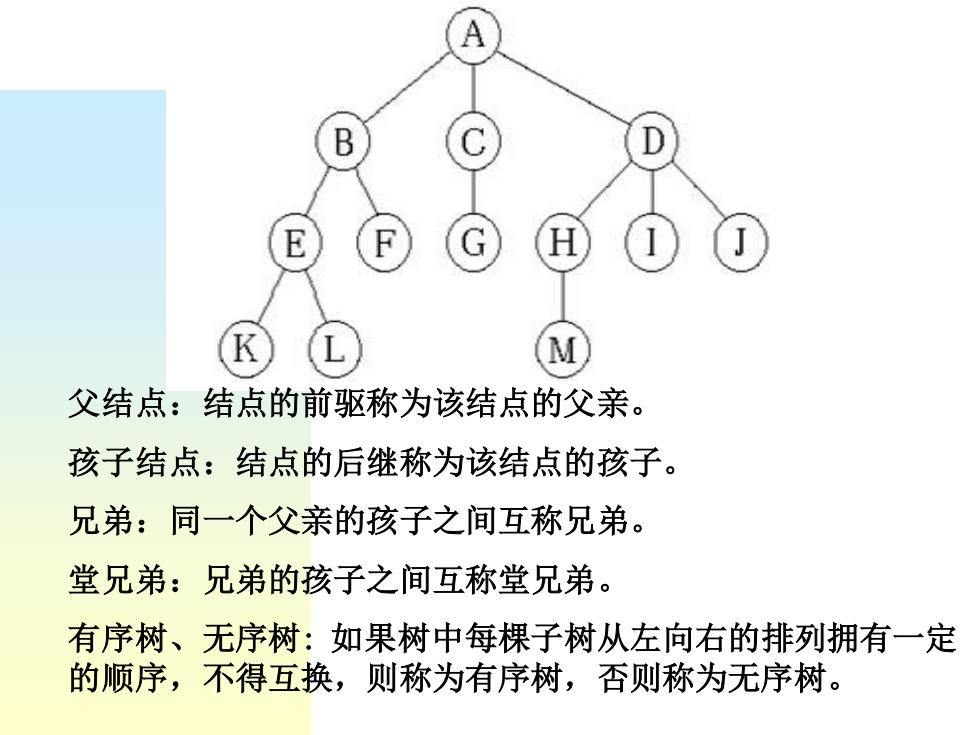
B 父结点:结点的前驱称为该结点的父亲。 孩子结点:结点的后继称为该结点的孩子。 兄弟:同一个父亲的孩子之间互称兄弟。 堂兄弟:兄弟的孩子之间互称堂兄弟。 有序树、无序树:如果树中每棵子树从左向右的排列拥有一定 的顺序,不得互换,则称为有序树,否则称为无序树
父结点:结点的前驱称为该结点的父亲。 孩子结点:结点的后继称为该结点的孩子。 兄弟:同一个父亲的孩子之间互称兄弟。 堂兄弟:兄弟的孩子之间互称堂兄弟。 有序树、无序树: 如果树中每棵子树从左向右的排列拥有一定 的顺序,不得互换,则称为有序树,否则称为无序树
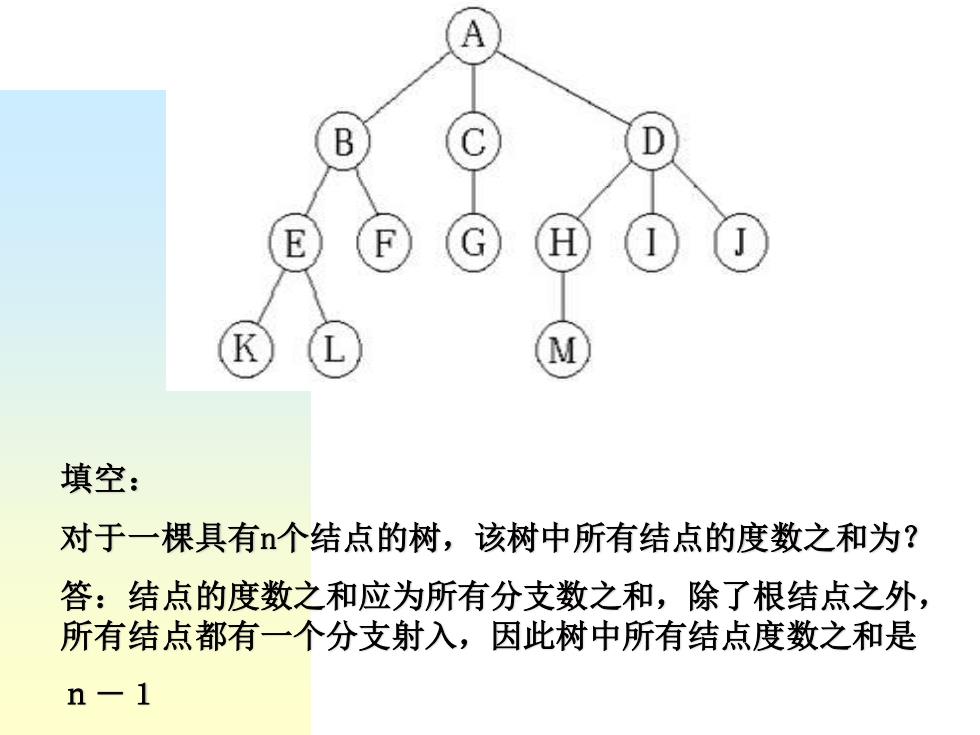
B 填空: 对于一棵具有个结点的树,该树中所有结点的度数之和为? 答:结点的度数之和应为所有分支数之和,除了根结点之外, 所有结点都有一个分支射入,因此树中所有结点度数之和是 n-1
填空: 对于一棵具有n个结点的树,该树中所有结点的度数之和为? 答:结点的度数之和应为所有分支数之和,除了根结点之外, 所有结点都有一个分支射入,因此树中所有结点度数之和是 n-1