
章 火图

在线性表中,结点之间的关系是线性 关系,除第一个结点和最后一个结点外, 每个结点只有一个前趋和一个后继
在线性表中,结点之间的关系是线性 关系,除第一个结点和最后一个结点外, 每个结点只有一个前趋和一个后继
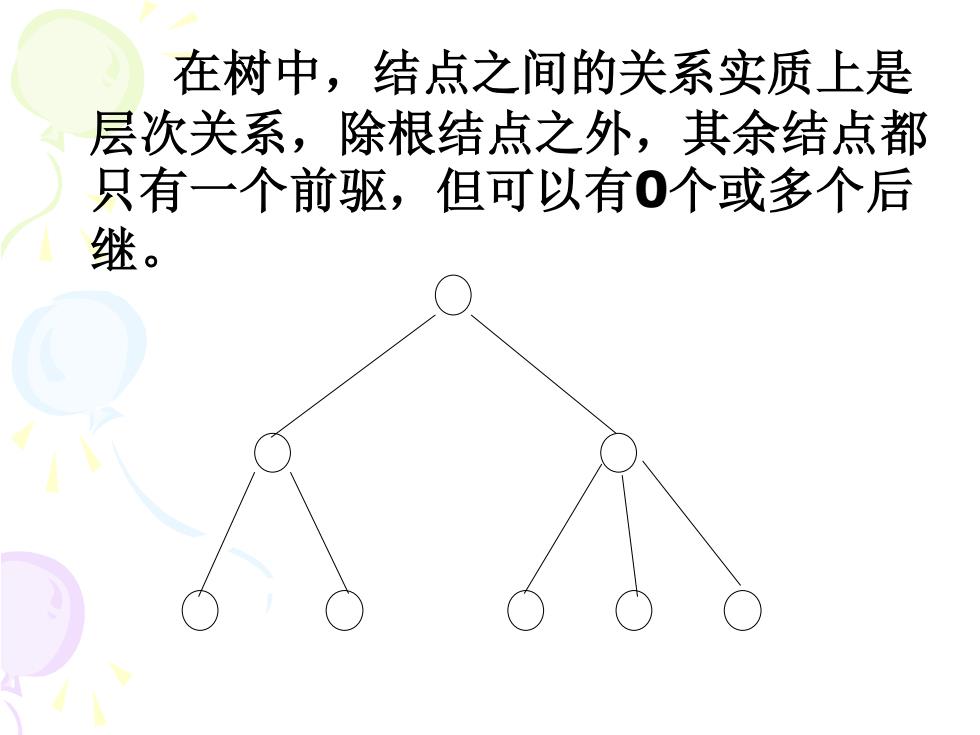
在树中,结点之间的关系实质上是 层次关系,除根结点之外,其余结点都 只有一个前驱,但可以有0个或多个后 继
在树中,结点之间的关系实质上是 层次关系,除根结点之外,其余结点都 只有一个前驱,但可以有0个或多个后 继

在图结构中,对结点的前趋和后继个 数都是不加限制的,即结点可以有0个或 多个前驱,也可以有0个或多个后继。 (结点之间的关系是任意的)
在图结构中,对结点的前趋和后继个 数都是不加限制的,即结点可以有0个或 多个前驱,也可以有0个或多个后继。 (结点之间的关系是任意的)
7.1图的定义和术语 1、有向图(直观的说:带箭头的就是有向图) v3 v4 顶点(vertex) 即图中的圆圈。该有向图 共有四个顶点:V1,V2,V3,V4. 弧(arc)即图中的箭头,也称有向边。该有 向图共有4条弧。记为
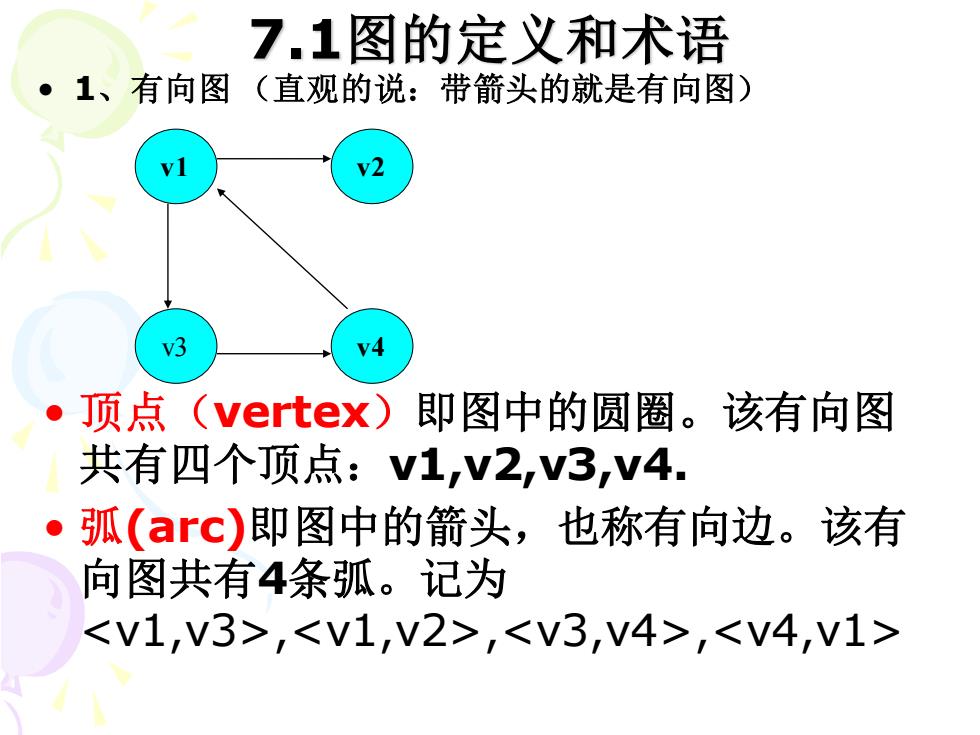
7.1图的定义和术语 • 1、有向图 (直观的说:带箭头的就是有向图) v1 v2 v3 v4 • 顶点(vertex)即图中的圆圈。该有向图 共有四个顶点:v1,v2,v3,v4. • 弧(arc)即图中的箭头,也称有向边。该有 向图共有4条弧。记为
v2 v3 v4 ·弧尾,弧头:弧的弧尾是v1,弧头是v3。 有向图的二元组描述:顶点的集合和弧的集合来描述 有向图。G1=(V,A)其中 V={v1,v2v3,v4}, A={
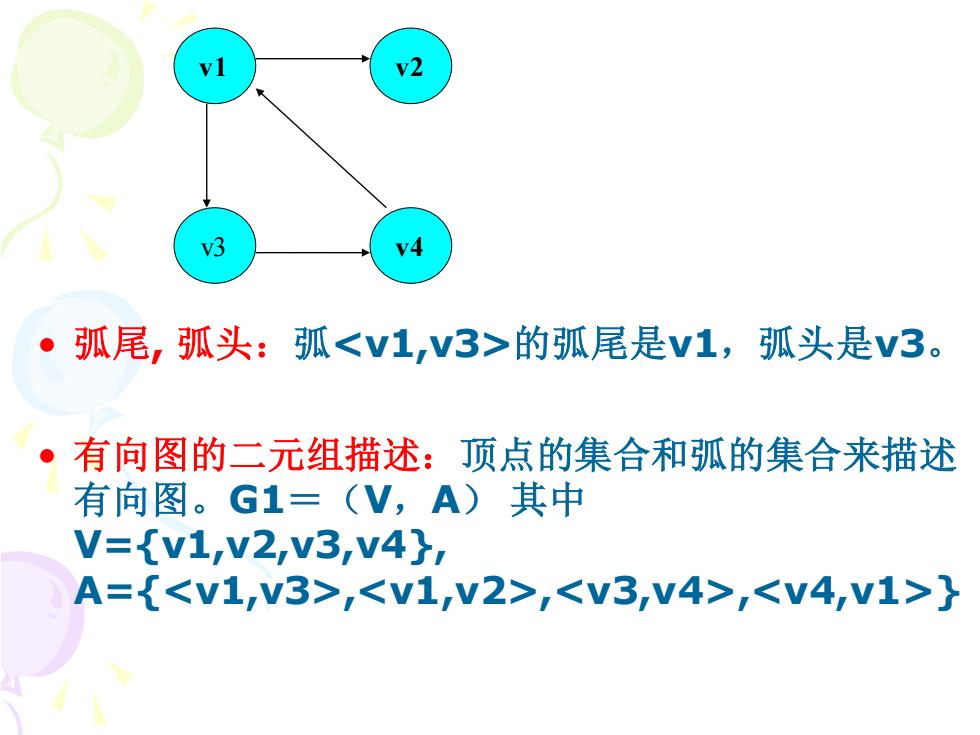
• 弧尾, 弧头:弧的弧尾是v1,弧头是v3。 • 有向图的二元组描述:顶点的集合和弧的集合来描述 有向图。G1=(V,A) 其中 V={v1,v2,v3,v4}, A={,,,} v1 v2 v3 v4
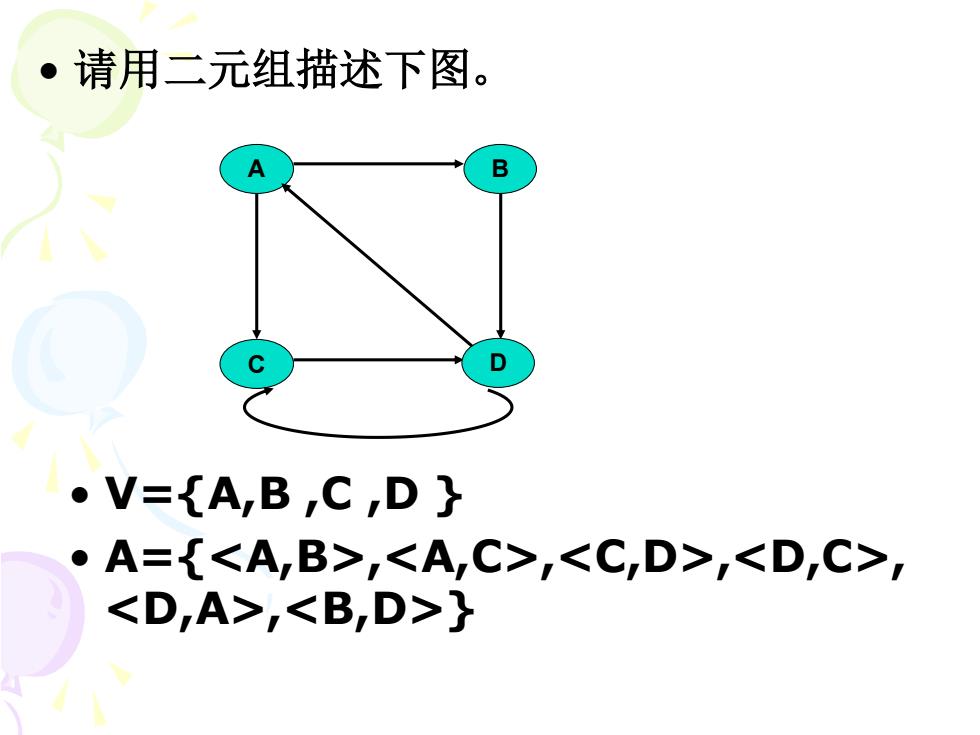
·请用二元组描述下图。 A B 。V={A,B,C,D} ·A={,,,, ,}
• 请用二元组描述下图。 A B C D • V={A,B ,C ,D } • A={,,,, ,}
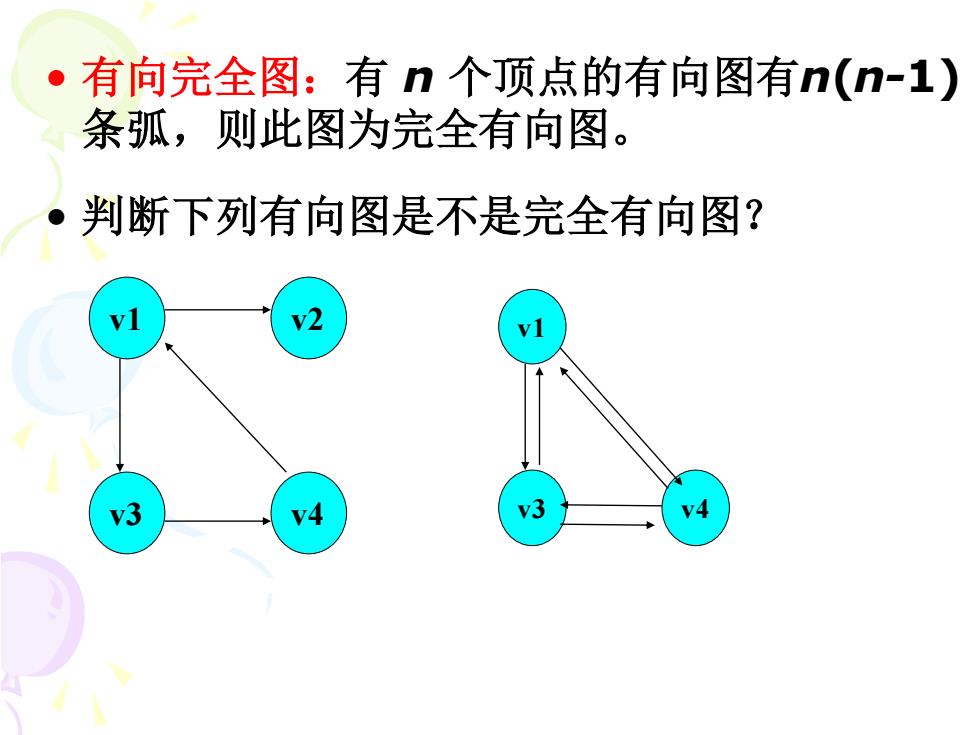
有向完全图:有n个顶点的有向图有n(n-1) 条弧,则此图为完全有向图。 判断下列有向图是不是完全有向图? v2 v3 v4 y3
• 有向完全图:有 n 个顶点的有向图有n(n-1) 条弧,则此图为完全有向图。 • 判断下列有向图是不是完全有向图? v1 v2 v3 v4 v1 v3 v4
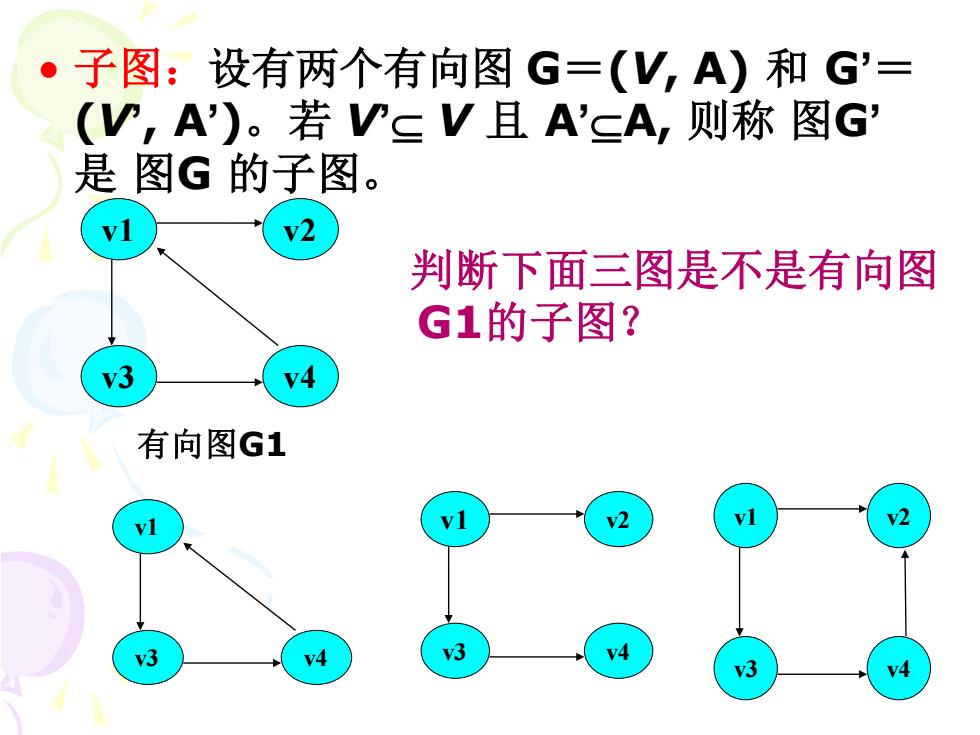
·子图:设有两个有向图G=(V,A)和G'= (V,A)。若VsV且A'∈A,则称图G 是图G的子图。 vl v2 判断下面三图是不是有向图 G1的子图? y3 有向图G1 vl v2 vl v2 y3 v4 v3 v4 v3
• 子图:设有两个有向图 G=(V, A) 和 G’= (V’, A’)。若 V’ V 且 A’A, 则称 图G’ 是 图G 的子图。 v1 v2 v3 v4 v1 v3 v4 v1 v2 v3 v4 v1 v2 v3 v4 有向图G1 判断下面三图是不是有向图 G1的子图?
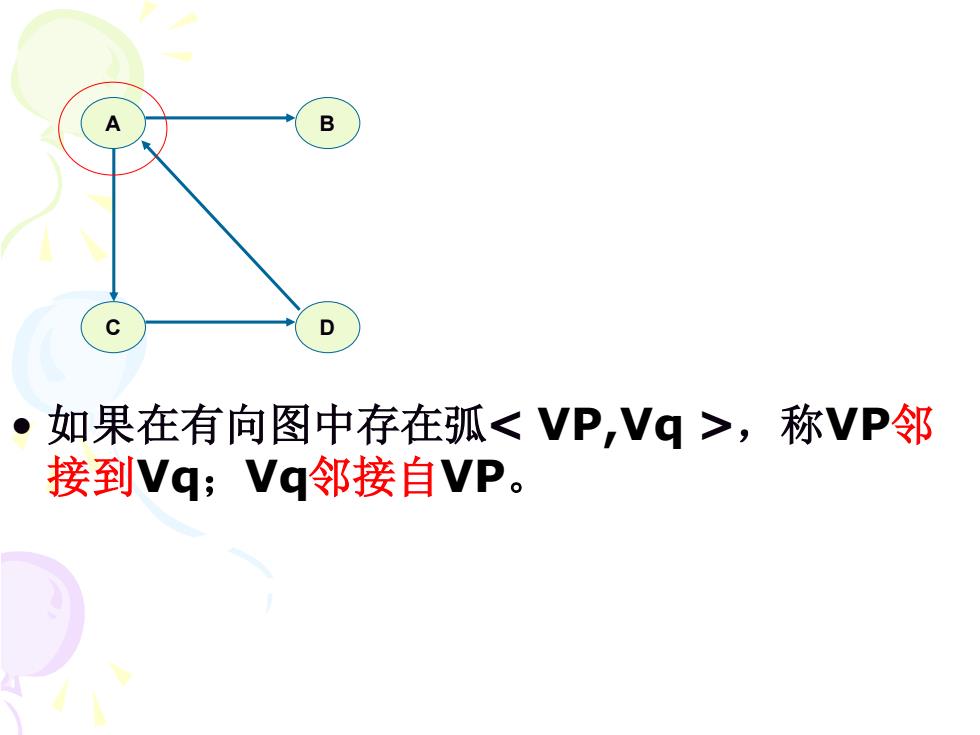
B C D 如果在有向图中存在弧,称VP邻 接到Vq;Vq邻接自VP
• 如果在有向图中存在弧,称VP邻 接到Vq;Vq邻接自VP。 A B C D