
基于角点特征的图像配准
基于角点特征的图像配准

课题的背景和选题依据 军事领域 我们身h Microsoft FUJITSU 10.d 2 Gaogle
2 课题的背景和选题依据 军事领域 我们身边 备受关注

图像配准方法现状 什么是图像配准? 图像配准技术是将不同时间、不同成像设备、不同拍摄 条件下获取的多幅图像进行某种意义上匹配的过程。 3
3 图像配准方法现状 什么是图像配准? 图像配准技术是将不同时间、不同成像设备、不同拍摄 条件下获取的多幅图像进行某种意义上匹配的过程

图像配准方法现状 目前研究关注的三个方面: 1.算法复杂度; 2.精度;。 本文关注 3.鲁棒性。 常用三类配准算法: 1.基于灰度的图像配准方法; 2.基于变换域的图像配准方法; 本文关注 4 3.基于特征的图像配准方法
4 图像配准方法现状 目前研究关注的三个方面: 1. 算法复杂度; 2. 精度; 3. 鲁棒性。 常用三类配准算法: 1. 基于灰度的图像配准方法; 2. 基于变换域的图像配准方法; 3. 基于特征的图像配准方法。 本文关注 本文关注
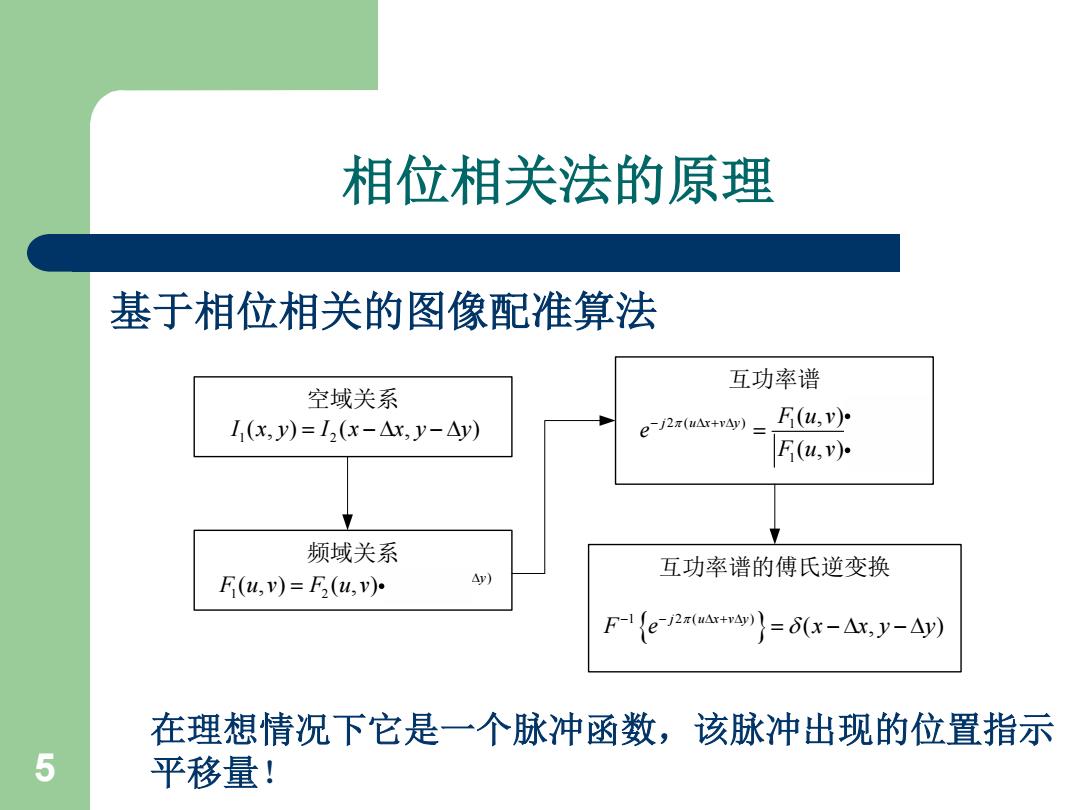
相位相关法的原理 基于相位相关的图像配准算法 互功率谱 空域关系 I1(x,y)=I2(x-△x,y-△y) eJ2x(uAr+vAy)) F(u,v少 F(u,v) 频域关系 F(u,v)=F(u,v). Ay) 互功率谱的傅氏逆变换 F-ie()=(x-Ax,y-Ay) 在理想情况下它是一个脉冲函数,该脉冲出现的位置指示 5 平移量!
5 相位相关法的原理 基于相位相关的图像配准算法 在理想情况下它是一个脉冲函数,该脉冲出现的位置指示 平移量! 1 2 I x y I x x y y ( , ) ( , ) 空域关系 2 ( ) 1 2 ( , ) ( , ) j u x v y F u v F u v e 频域关系 * 2 ( ) 1 2 * 1 2 ( , ) ( , ) ( , ) ( , ) j u x v y F u v F u v e F u v F u v 互功率谱 1 2 ( ) ( , ) j u x v y F e x x y y 互功率谱的傅氏逆变换
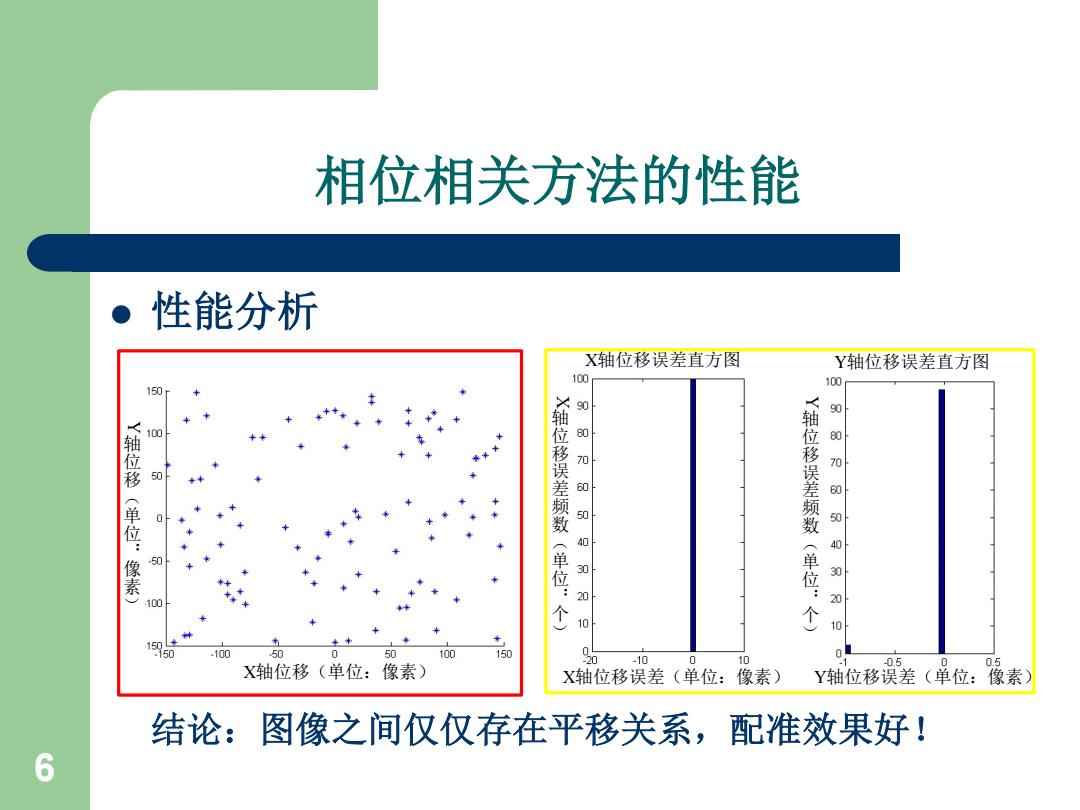
相位相关方法的性能 性能分析 X轴位移误差直方图 Y轴位移误差直方图 100 100 150 轴位移 100 (单位:像素) 50 轴位移误差频数(单位:个) 0000000010 轴位移误差频数(单位:个) 000004 100 第010 150 50 100 50 0 50 100 150 .10 10 X轴位移(单位:像素) X轴位移误差(单位:像素) Y轴位移误差(单位:像素) 结论:图像之间仅仅存在平移关系,配准效果好! 6
6 相位相关方法的性能 性能分析 结论:图像之间仅仅存在平移关系,配准效果好! X轴位移误差(单位:像素) Y轴位移误差(单位:像素) X 轴 位 移 误 差 频 数 ( 单 位 : 个 ) Y 轴 位 移 误 差 频 数 ( 单 位 : 个 ) X轴位移误差直方图 Y轴位移误差直方图 X轴位移(单位:像素) Y 轴 位 移 ( 单 位 : 像 素 )

相位相关法的缺点 相位相关 参数估计! 配准错误! 源图像 (参考图 目标图像 像) 相 (a).参考图像 (b).目标图像 够解 转制 问题 配准部分 相位相关 函数 00 (c).配准图像 (d).相位相关函数 77 正确配准
7 相位相关法的缺点 相位相关法的缺陷:无法解决旋转参数估计! 相位相关法:不能解决具有 旋转关系的参数估计问题 极坐标相位相关法:能够解 决旋转关系的图像配准问题 配准错误! 正确配准 源图像 (参考图 像) 目标图像 配准部分 相位相关 函数
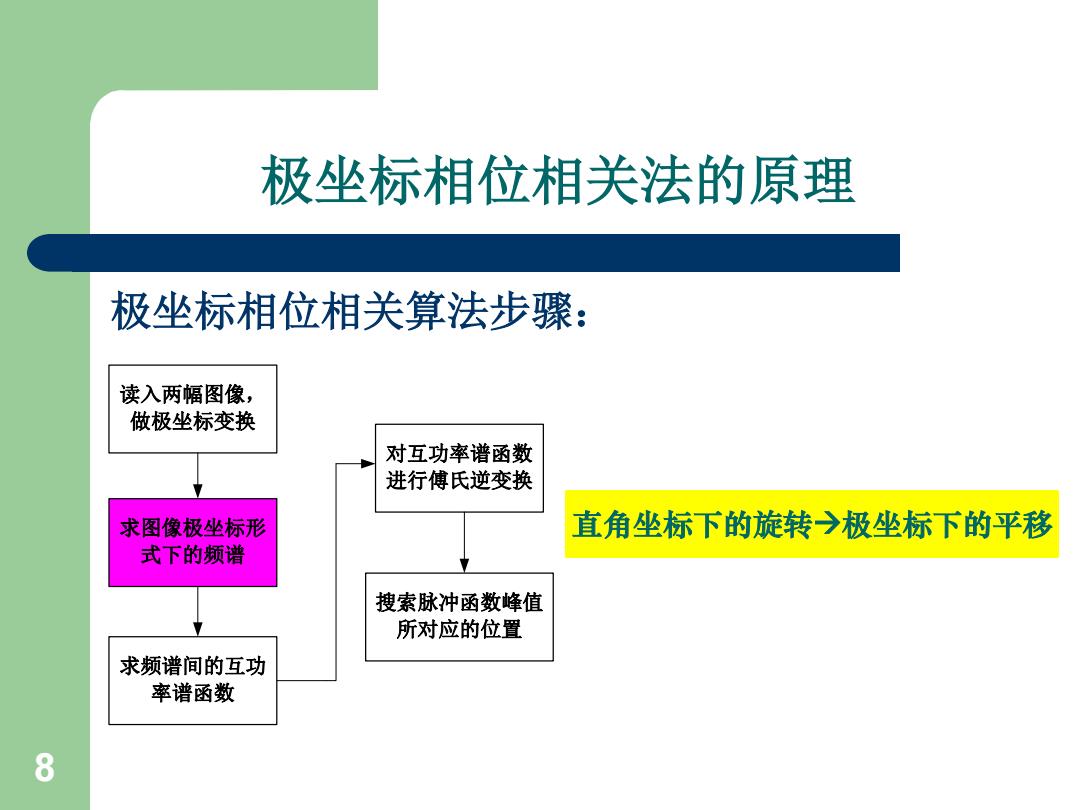
极坐标相位相关法的原理 极坐标相位相关算法步骤: 读入两幅图像, 做极坐标变换 对互功率谱函数 进行傅氏逆变换 求图像极坐标形 直角坐标下的旋转→极坐标下的平移 式下的频谱 搜索脉冲函数峰值 所对应的位置 求频谱间的互功 率谱函数 8
8 极坐标相位相关法的原理 极坐标相位相关算法步骤: 读入两幅图像, 做极坐标变换 求图像极坐标形 式下的频谱 求频谱间的互功 率谱函数 对互功率谱函数 进行傅氏逆变换 搜索脉冲函数峰值 所对应的位置 直角坐标下的旋转极坐标下的平移

极坐标相位相关法的缺点 极坐标相位相关法存在的问题: 必须事先知道旋转的中心或必须固定好一个旋转中心。 而实际上图像旋转的中心一般是很难提前知道! 极坐标相位相关法:需预知 极坐标相位相关法的改进: 图像旋转中心 无需预知图像旋转中心 9
9 极坐标相位相关法的缺点 极坐标相位相关法存在的问题: 必须事先知道旋转的中心或必须固定好一个旋转中心。 而实际上图像旋转的中心一般是很难提前知道! 极坐标相位相关法的改进: 无需预知图像旋转中心 极坐标相位相关法:需预知 图像旋转中心

极坐标相位相关法的改进 计算两幅图像的 问题出现了: 频谱幅值 (a以.参考图像 象在旋转、平移时将 仂率谱 |入更多新的内容, 信息会对直角坐标 求频谱幅值的极 (c以.参考图像图像類谱幅值 坐标变换 际余下的频域 南付 真实:20° )参图像图像類襟幅值极坐标变换 实测: 60° 代诬受预像度系极坐标变换 计算频谱幅值极 长 坐标形式下的傅 00 氏变换 10 (g)两幅图像频谱幅值极坐标变换后的相关函数
10 极坐标相位相关法的改进 新的问题出现了: 图像在旋转、平移时将 会引入更多新的内容, 这些信息会对直角坐标 系下的频域产生干扰, 严重影响估计值的准确 度 。 计算两幅图像的 频谱幅值 求频谱幅值的极 坐标变换 计算频谱幅值极 坐标形式下的傅 氏变换 求互功率谱 求互功率谱的傅 氏逆变换,搜索 峰值对应位置 (a).参考图像 (b).目标图像 (c).参考图像图像频谱幅值 (d).目标图像图像频谱幅值 (e).参考图像图像频谱幅值极坐标变换 (f).目标图像图像频谱幅值极坐标变换 (g).两幅图像频谱幅值极坐标变换后的相关函数 真实:20° 实测:60°