《物理化学》课程教学课件（讲稿，AⅠ）第6章 化学平衡

第六章化学平衡 范霍夫平箱 3 dD+eE±+gG P'D PE P'F P'G

第六章 化学平衡

第六章化学平衡 §6.1化学反应的平衡条件 反应进度和化学反应的亲和势 §6.2化学反应的平衡常数和等温方程式 §6.3平衡常数的表示式 §6.4复相化学平衡 §6.5标准摩尔生成Gibbs自由能 §6.6温度、压力及惰性气体对化学平衡的影响 §6.7同时化学平衡 §6.8反应的耦合 §6.9近似计算 *§6.10生物能学简介

第六章 化学平衡 §6.1 化学反应的平衡条件—— 反应进度和化学反应的亲和势 §6.2 化学反应的平衡常数和等温方程式 §6.3 平衡常数的表示式 §6.4 复相化学平衡 §6.5 标准摩尔生成Gibbs自由能 §6.6 温度、压力及惰性气体对化学平衡的影响 §6.8 反应的耦合 §6.9 近似计算 §6.7 同时化学平衡 *§6.10 生物能学简介

§6.1 化学反应的平衡条件— 反应进度和化学反应的亲和势 化学反应的平衡条件和反应进度5的关系 化学反应的亲和势

§6.1 化学反应的平衡条件—— 反应进度和化学反应的亲和势 化学反应的亲和势 化学反应的平衡条件和反应进度  的关系

1.化学反应的平衡条件和反应进度号的关系 封闭的单相多组分体系，不作非膨胀功，当发生了一 个微小变化时，有： dG=-SdT+dp+∑4edng Q 化学反应系统：引入反应进度的概念 dξ= dns dne Veds

1.化学反应的平衡条件和反应进度  的关系 封闭的单相多组分体系，不作非膨胀功，当发生了一 个微小变化时，有： B B d d d d G S T V p n = − + + B 化学反应系统：引入反应进度的概念 B B d d n   = d d nB B = 

化学反应的平衡条件和反应进度ξ的关系 基本公式可表示为： dG=-Sd7+dp+∑s4d5 等温、等压条件下， (dG,p=∑hdn:=∑4ed与

化学反应的平衡条件和反应进度  的关系 基本公式可表示为： B B B d d d d G S T V p = − + +   等温、等压条件下， , B B B （ ）d d G n T p = B B B =  d

化学反应的平衡条件和反应进度ξ的关系 (dGr,p=∑4d5 说明： (1)适用于等温、等压、不作非膨胀功的化学反应； (2)适用于某个反应进度或时刻时反应方向的判断， 此时，需保证各物质的化学势4有定值

化学反应的平衡条件和反应进度  的关系 , B B B （d d G）T p =   B B r m T p, B G   G       = =      说明： （1）适用于等温、等压、不作非膨胀功的化学反应； （2）适用于某个反应进度或时刻时反应方向的判断， 此时，需保证各物质的化学势  B 有定值

判断化学反应的方向与限度 用( G,24,或aGh,作判据都是等效的 (A.Gm).0 反应自发地向左进行 ∑Yh>0 (A.Gm)T,p=0 反应达到平衡 Σ40

判断化学反应的方向与限度 用 , B r m , 作判据都是等效的 B ( ) , ( ) T p B T p G   G      或 r m , ( ) 0  G T p  反应自发地向右进行 r m , ( ) 0  G T p  反应自发地向左进行 r m , ( ) 0  G T p = 反应达到平衡 B B B    0 B B B   > 0 B B B   = 0

判断化学反应的方向与限度 用 判断，这相当于G~5图上曲线的斜率 ，p 0 反应自发向左进行，趋向平衡 og aG =0 )T.P 反应达到平衡

判断化学反应的方向与限度 用 判断，这相当于 图上曲线的斜率 T p, G          G ~  , 0 T p G           反应自发向右进行，趋向平衡 , 0 T p G           反应自发向左进行，趋向平衡 , 0 T p G         =  反应达到平衡

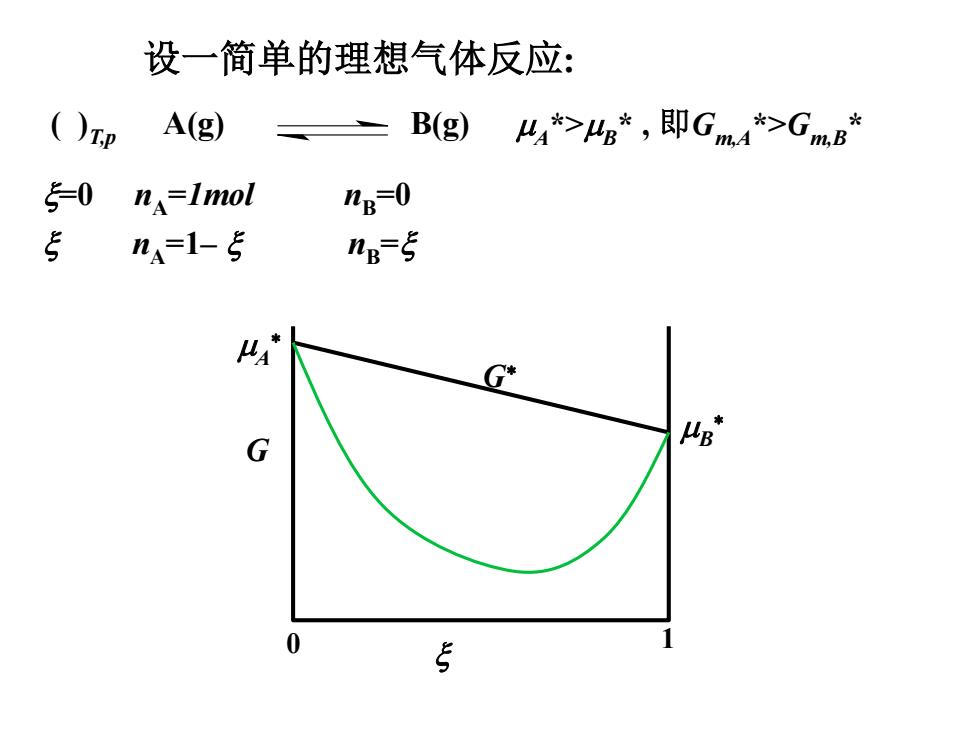
设一简单的理想气体反应： （)p A(g) B(g）4*>4s*,即Gm4*>GmB* 50 nA=Imol nB-0 5 na-1-5 ng-5 G* G 0 5

设一简单的理想气体反应: =0 nA =1mol nB =0  nA =1–  nB = ( )T,p A(g) B(g) A *>B * , 即Gm,A*>Gm,B * G G 0 1  A  B 

为什么化学反应通常不能进行到底？ 都向着系统Gibbs自由能降低的方向进行。 0反应正向自发； =0反应达平衡，5=g(限度)； >0反应逆向自发。 反应平衡条件： ()np（W0） (△，Gm)z,p=∑YB4B=0 G 59 10

10 反应平衡条件: ( )T,p（Wf =0） 为什么化学反应通常不能进行到底？ T,p ξ G         , ( ) 0  = = r m T p B B G   都向着系统Gibbs自由能降低的方向进行。 0 反应逆向自发。 G  eq 0 1  A  B  0 ,          T p G   0 , =         T p G   0 ,          T p G  