《数字信号处理》课程教学课件（PPT讲稿）ch2_1 DFT

离散傅里叶变换共问题的提出共有限长序列的傅里叶分析其离散傅里叶变换的性质#利用DFT计算线性卷积#利用DFT分析信号的频谱崔丽珍7/2/2025内蒙古科技大学

7/2/2025 内蒙古科技大学 崔丽珍 离散傅里叶变换 问题的提出 有限长序列的傅里叶分析 离散傅里叶变换的性质 利用DFT计算线性卷积 利用DFT分析信号的频谱

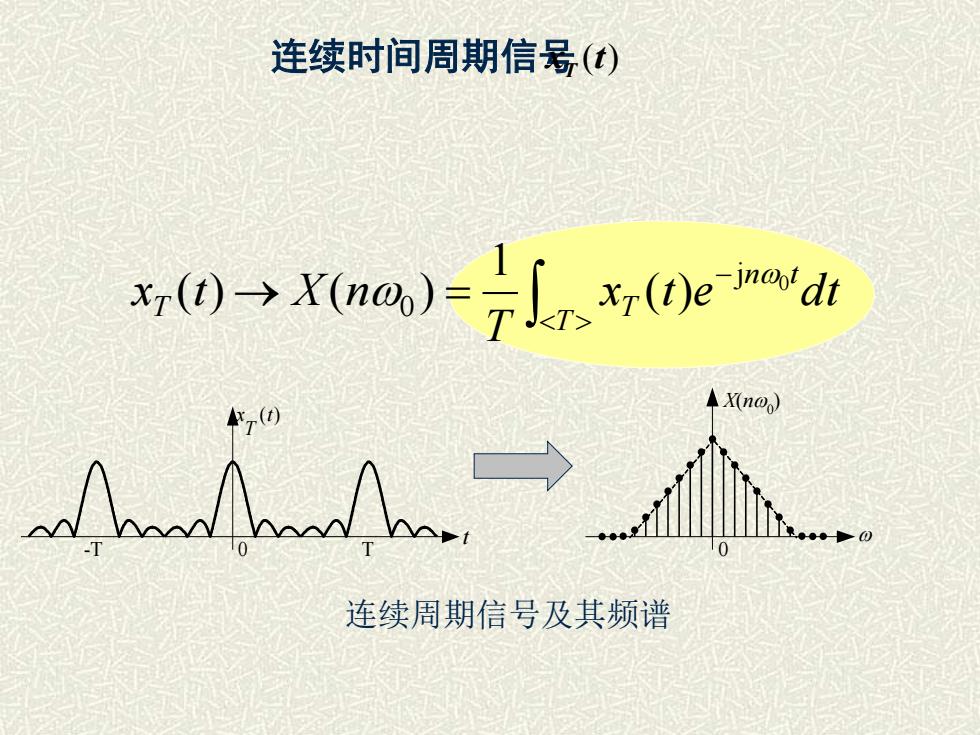
有限长序列的傅里叶分析四种信号傅里叶表示强1.周期为T.的连续时间周期信号ZX(no.) ejinox(t) =n=-0X(t) ·e-jnoo' dtX(n0) =频谱特点：离散非周期谱崔丽珍7/2/2025内蒙古科技大学

7/2/2025 内蒙古科技大学 崔丽珍 有限长序列的傅里叶分析 一、四种信号傅里叶表示 1. 周期为T0的连续时间周期信号   =− =  n n t x t X n e 0 j 0 ( ) ( ) ~   x t e dt T X n n t T 0 0 j 0 0 ( ) 1 ~ ( )   −   =   频谱特点： 离散非周期谱

连续时间周期信号（t专Xr(t)e-jnoo' dtx-(t) → X(noo) X(no)ST连续周期信号及其频谱

连续时间周期信号 x (t) T   − → = T n t T xT t e d t T x t X n 0 j 0 ( ) 1 ( ) ( )   t 0 (t) T x -T T  X(n0 ) 0 连续周期信号及其频谱

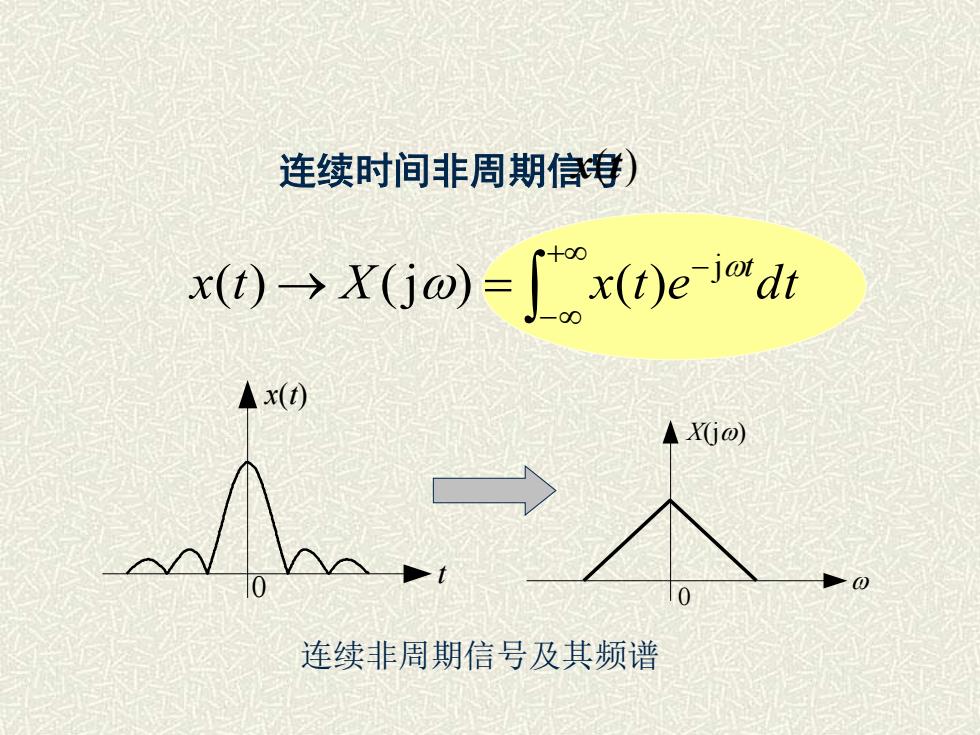
2.连续时间非周期信号1X(jo) ejotdox(t)-2元X(jo)= ( x(t)e-jotdt频谱特点：连续非周期谱崔丽珍7/2/2025内蒙古科技大学

7/2/2025 内蒙古科技大学 崔丽珍 2. 连续时间非周期信号     x t X e d j t (j ) 2 1 ( ) =   + − X x t e dt j t (j ) ( )   − + − =  频谱特点： 连续非周期谱

连续时间非周期信#x(t) - X(jo) = f- x(t)e-jo dtA x(t) X(jo)20连续非周期信号及其频谱

连续时间非周期信号 x(t)  + − − x t → X = x t e d t t  j ( ) (j ) ( ) t x(t) 0  X(j) 0 连续非周期信号及其频谱

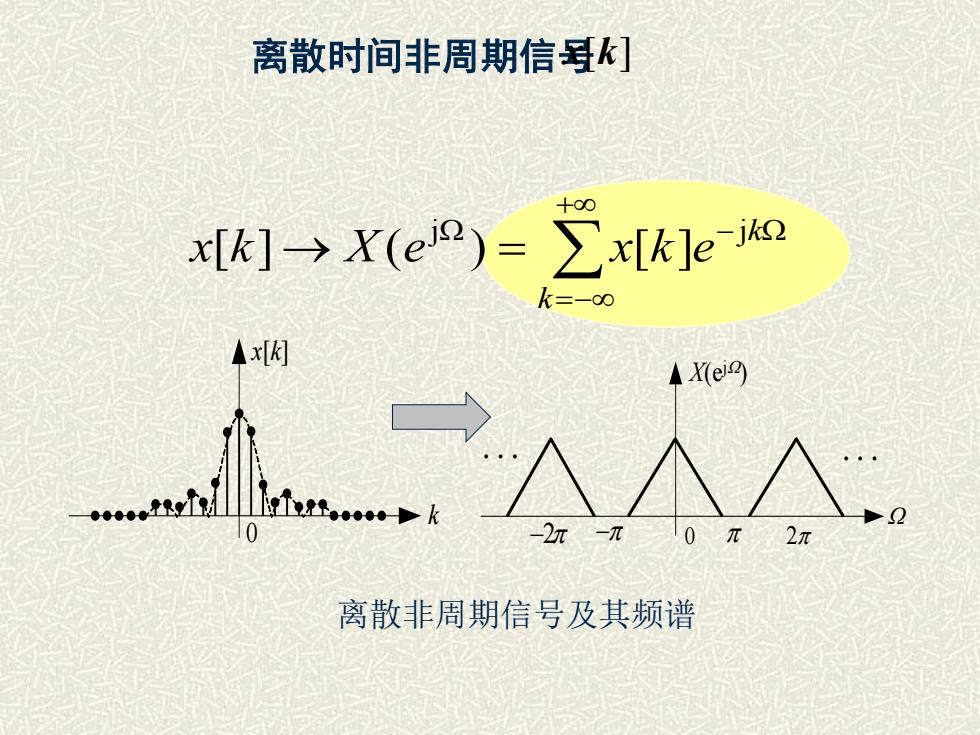
离散非周期信号X(ej?)·ejko dQx[k]= IDTFT[X(e}T2元X(e19)-DTFT([k]) - Zx[k]-e-iok=-00频谱特点：周期为2元的连续谱崔丽珍7/2/2025内蒙古科技大学

7/2/2025 内蒙古科技大学 崔丽珍 3. 离散非周期信号 = =    −    x k X e X e e d j j jk ( ) 2 1 [ ] IDTFT[ ( )      =−  = =   k k X e x k x k e j -j ( ) DTFT{ [ ]} [ ] 频谱特点： 周期为2的连续谱

离散时间非周期信号k+8x[k]e-jk?x[k]→X(ejg)= k=-00A x[k]X(eid)0-2元一元0福元2元离散非周期信号及其频谱

离散时间非周期信号 x[k]  + =−  −  → = k k x k X e x k e j j [ ] ( ) [ ] k x[k] 0  X(ej ) 0 . . −2 −  2 离散非周期信号及其频谱

周期为N的离散周期信号2元mkN-1W71ZX[m] W-mkNx[k]= IDFS(X[m])X[m]·e1-ANNm=0m=02元N-1N-1mkN2x[k].wX[m] = DFS(x[k]} = Zx[k] -ek=0k=0频谱特点：周期为N的离散谱崔丽珍7/2/2025内蒙古科技大学

7/2/2025 内蒙古科技大学 崔丽珍 4. 周期为N 的离散周期信号 m k N N m m k N N m X m W N X m e N x k X m − − = − = = =   =   1 0 2 j 1 0 [ ] 1 ~ [ ] 1 ~ [ ]} ~ [ ] IDFS{ ~  km N N k m k N N k X m = x k = x k e = x k W − = − = 1 0 2 -j 1 0 [ ] ~ [ ] ~ [ ] DFS{ [ ]} ~  频谱特点：周期为N的离散谱

离散时间周期信号[k]2元2mkNx[k]-→>X[m]=x[k]ek=0AX[m]Ax[k]ik-NN-N1N离散周期信号及其频谱

离散时间周期信号 [ ] ~ x k  − = − → = 1 0 2 j [ ] ~ [ ] ~ [ ] ~ N k mk N x k X m x k e  0 [ ] ~x k k -N N 离散周期信号及其频谱 m [ ] ~ X m -N 0 N .

四种信号的时域与频域对应关系At)XjoFxtFSXeix[K]DTFT2元2元AX[m][K]DFS

t x(t) 0  X(j) 0 t 0 ( ) ~x t k x[k] 0 0 [ ] ~x k k 四种信号的时域与频域对应关系  X(ej ) 0 . . −2 −  2 m [ ] ~ X m -N 0 N . .  X(n0 ) 0 FT FS DTFT DFS