
第十章纤维的力学性质 教学目标: 1、使学生了解纤维的基本力学性质, 2、使学生掌握纤维力学性质的表征指标及其表征方法。 3、使学生掌握纤维力学性质的诸多影响因素。 教学重点与难点: 教学重点:1、纤维各种力学现象形成机理、力学性能指标及影响因素。 2、基本力学模型 3、纤维的力学性质特征曲线及表征。 教学难点:纤维的拉伸变形曲线、纤维蠕变及蠕变回复曲线的理解和掌握 教学与学习建议: 1、教学建议 授课形式:讲解与讨论,实验 理论讲解织物的多种力学现象形成机理、力学性能指标及影响因素:通过举 例详细讲解纤维的力学性质特征曲线及其表征: 充分做好实验准备。 2、学习建议 通过实验室力学实验掌握纤维力学现象形成机理: 通过记忆和理解,掌握纤维的力学性能指标及其影响因素: 通过实验与理论的结合掌握纤维的力学性质特征曲线及其表征
第十章 纤维的力学性质 教学目标: 1、使学生了解纤维的基本力学性质。 2、使学生掌握纤维力学性质的表征指标及其表征方法。 3、使学生掌握纤维力学性质的诸多影响因素。 教学重点与难点: 教学重点:1、纤维各种力学现象形成机理、力学性能指标及影响因素。 2、基本力学模型 3、纤维的力学性质特征曲线及表征。 教学难点:纤维的拉伸变形曲线、纤维蠕变及蠕变回复曲线的理解和掌握 教学与学习建议: 1、教学建议 授课形式:讲解与讨论,实验 理论讲解织物的多种力学现象形成机理、力学性能指标及影响因素;通过举 例详细讲解纤维的力学性质特征曲线及其表征; 充分做好实验准备。 2、学习建议 通过实验室力学实验掌握纤维力学现象形成机理; 通过记忆和理解,掌握纤维的力学性能指标及其影响因素; 通过实验与理论的结合掌握纤维的力学性质特征曲线及其表征

第十章纤维的力学性质 第一节拉伸性质 一、纤维拉伸断裂性能的基本指标 1.拉仲断裂强力 断裂强力:又称绝对强力。它是指纤维能承受的最大拉伸外力,或单根纤维受外力 拉伸到断裂时所需要的力,单位为牛顿)。 2。湘对强度 纤维粗细不同时,强力也不同,因而对于不同粗细的纤维,强力没有可比性。为了便于 比较,可以将强力拆合成规定粗细时的力,这就是相对强度。常用的有三种: (1)断裂应力o,O。:为单位截面积上纤维能承受的最大拉力,标准单位为NWm(即帕) 常用Nmm(即兆帕Ma)表示。 (2)断裂强度(相对强度)p6:简称比强度或比应力,它是指每特(或每旦)纤维能承受的 最大拉力,单位为N/tex,常用cN/dtex(或cN/d)。 (3)断裂长度:纤维重力等于其断裂强力时的纤维长度,单位为km。 (4)以上三类相对强度的表达式分别为 0 g 3.断裂仲长 任何材料在受力作用的同时一般都会产生变形,这两者总是同时存在、同时发展的。在 拉伸力的作用下,材料一般要伸长。纤维拉伸到断裂时的伸长率(应变率),叫断裂伸长率, 或者断裂伸长度,用表示,单位为百分数 6=-Lx100% Lo 4.拉仲变形曲线和相关指标 (1)拉伸变形曲线 纤维的拉伸曲线有两种形式,即负荷p一伸长△1曲线和应力。一应变曲线。如图51 所示 2)相关指标 a.屈服点:图10-1中曲线上的Y点叫屈服点,这一点对应的拉伸应力叫屈服应力。 b.初始模量:指纤维拉伸曲线的起始部分直线段的应力与应变的比值,即σ-S曲线在起 始段的斜率。初始模量的大小表示纤维在小负荷作用下变形的难易程度,即纤维的刚性。 .断裂功:是指拉伸纤维至断裂时外力所作的功,是纤维材料抵抗外力破坏所具有的能 量。 d.断裂比功W:一是拉断单位体积纤维所需作的功W,单位为N/m。另一定义是重 量断裂比功W,是指拉断单位线密度与单位长度纤维材料所需做的功。 )和断裂伸长(△b)的乘积之比。 维材料的坚牢度和耐用性能
第十章 纤维的力学性质 第一节 拉伸性质 一、纤维拉伸断裂性能的基本指标: 1.拉伸断裂强力 断裂强力 pb : 又称绝对强力。它是指纤维能承受的最大拉伸外力,或单根纤维受外力 拉伸到断裂时所需要的力,单位为牛顿(N)。 2.相对强度 纤维粗细不同时,强力也不同,因而对于不同粗细的纤维,强力没有可比性。为了便于 比较,可以将强力拆合成规定粗细时的力,这就是相对强度。常用的有三种: (1)断裂应力 b b :为单位截面积上纤维能承受的最大拉力,标准单位为 N/m2 (即帕) 常用 N/mm2 (即兆帕 Mpa )表示。 (2)断裂强度(相对强度) pb :简称比强度或比应力,它是指每特(或每旦)纤维能承受的 最大拉力,单位为 N/tex,常用 cN/dtex(或 cN/d)。 (3)断裂长度 Lb:纤维重力等于其断裂强力时的纤维长度,单位为 km。 (4)以上三类相对强度的表达式分别为 b b A P = den b den tex b tex N P p N P p = = g m b b N P L = 3.断裂伸长 任何材料在受力作用的同时一般都会产生变形,这两者总是同时存在、同时发展的。在 拉伸力的作用下,材料一般要伸长。纤维拉伸到断裂时的伸长率(应变率),叫断裂伸长率, 或者断裂伸长度,用 a 表示,单位为百分数。 0 0 100(%) a a L L L − = 4.拉伸变形曲线和相关指标 (1)拉伸变形曲线 纤维的拉伸曲线有两种形式,即负荷 p-伸长△l 曲线和应力-应变曲线。如图 5-1 所示: (2)相关指标 a.屈服点:图 10-1 中曲线上的 Y 点叫屈服点,这一点对应的拉伸应力叫屈服应力。 b. 初始模量:指纤维拉伸曲线的起始部分直线段的应力与应变的比值,即 - 曲线在起 始段的斜率。初始模量的大小表示纤维在小负荷作用下变形的难易程度,即纤维的刚性。 c.断裂功W:是指拉伸纤维至断裂时外力所作的功,是纤维材料抵抗外力破坏所具有的能 量。 d.断裂比功 Wv :一是拉断单位体积纤维所需作的功 Wv ,单位为N/mm2。另一定义是重 量断裂比功 Ww ,是指拉断单位线密度与单位长度纤维材料所需做的功。 e.功系数η:指纤维的断裂功与断裂强力( pb )和断裂伸长( lb )的乘积之比。 其中c、d、e都属于断裂功指标,断裂功是强力和伸长的综合指标,它可以有效地评定纤 维材料的坚牢度和耐用性能
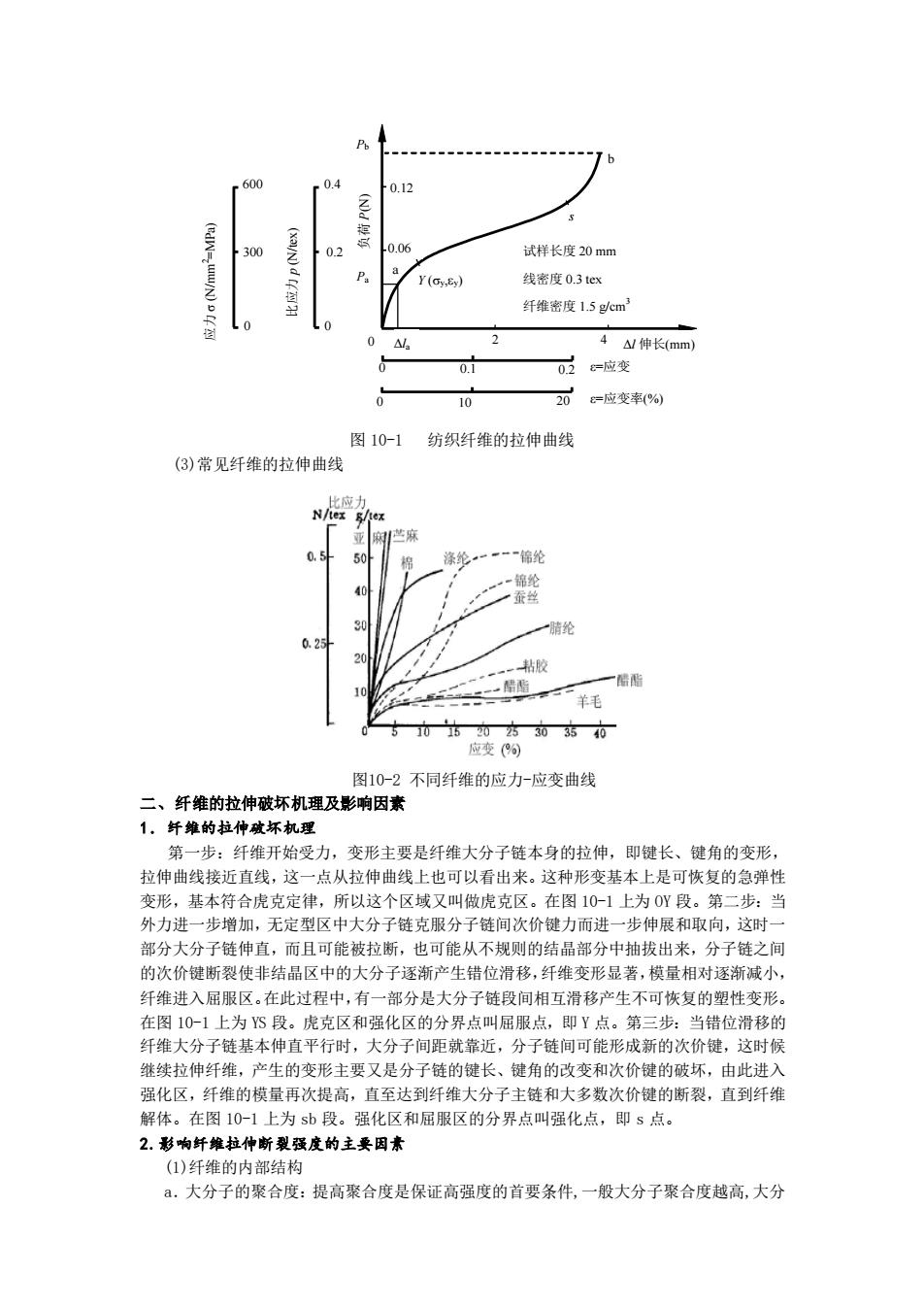
试样长度20m 线整度0.3tex 纤维密度15cm 伸长mm 0.1 038-应变 10 20=应变率(% 图10-1 纺织纤维的拉伸曲线 (3)常见纤维的拉伸曲线 感麻 锦纶 蚕 0.2 一酯 羊手 图10-2不同纤维的应力-应变曲线 二、纤维的拉伸破坏机理及影响因素 1。纤维的拉仲破坏机理 一步:纤维开始受力,变形主要是纤维大分子链本身的拉伸,即键长、键角的变形 拉伸曲线接近直线,这一点从拉伸曲线上也可以看出来。这种形变基本上是可恢复的急弹性 变形,基本符合虎克定律,所以这个区域又叫做虎克区。在图101上为O吖段。第二步:当 外力进一步增加,无定型区中大分子链克服分子链间次价键力而进一步伸展和取向,这时 部分大分子链伸直,而且可能被拉断,也可能从不规则的结晶部分中抽拔出来,分子链之间 的次价健断裂使非结品区中的大分子逐渐产生错位滑移,纤维变形显著,模量相对逐渐减小 纤维进入屈服区。在此过程中,有一部分是大分子链段间相互滑移产生不可恢复的塑性变形 在图10-1上为S段。虎克区和强化区的分界点叫屈服点,即Y点。第三步:当错位滑移的 纤维大分子链基本伸直平行时,大分子间距就靠近,分子链间可能形成新的次价健,这时候 继续拉伸纤维,产生的变形主要又是分子链的键长、键角的改变和次价键的破坏,由此进入 强化区,纤维的模量再次提高,直至达到纤维大分子主键 大多数次价键的断裂,直到纤维 解体。在图10-1上为sb段。强化区和屈服区的分界点叫强化点,即s点。 2.衫响纤维拉仲断覆强度的主要因素 (1)纤维的内部结构 a,大分子的聚合度:提高聚合度是保证高强度的首要条件,一般大分子聚合度越高,大分
a Y (y,y) s Pb b 0.06 0.12 Pa负荷 P(N) Δla 2 4 0 Δl 伸长(mm) 0 0.1 0.2 0 10 20 ε=应变 ε=应变率(%) 比应力 p (N/tex) 0 0.2 0.4 应力 σ (N/mm 2=MPa) 0 300 600 试样长度 20 mm 线密度 0.3 tex 纤维密度 1.5 g/cm3 图 10-1 纺织纤维的拉伸曲线 (3)常见纤维的拉伸曲线 图10-2 不同纤维的应力-应变曲线 二、纤维的拉伸破坏机理及影响因素 1.纤维的拉伸破坏机理 第一步:纤维开始受力,变形主要是纤维大分子链本身的拉伸,即键长、键角的变形, 拉伸曲线接近直线,这一点从拉伸曲线上也可以看出来。这种形变基本上是可恢复的急弹性 变形,基本符合虎克定律,所以这个区域又叫做虎克区。在图 10-1 上为 OY 段。第二步:当 外力进一步增加,无定型区中大分子链克服分子链间次价键力而进一步伸展和取向,这时一 部分大分子链伸直,而且可能被拉断,也可能从不规则的结晶部分中抽拔出来,分子链之间 的次价键断裂使非结晶区中的大分子逐渐产生错位滑移,纤维变形显著,模量相对逐渐减小, 纤维进入屈服区。在此过程中,有一部分是大分子链段间相互滑移产生不可恢复的塑性变形。 在图 10-1 上为 YS 段。虎克区和强化区的分界点叫屈服点,即 Y 点。第三步:当错位滑移的 纤维大分子链基本伸直平行时,大分子间距就靠近,分子链间可能形成新的次价键,这时候 继续拉伸纤维,产生的变形主要又是分子链的键长、键角的改变和次价键的破坏,由此进入 强化区,纤维的模量再次提高,直至达到纤维大分子主链和大多数次价键的断裂,直到纤维 解体。在图 10-1 上为 sb 段。强化区和屈服区的分界点叫强化点,即 s 点。 2.影响纤维拉伸断裂强度的主要因素 (1)纤维的内部结构 a.大分子的聚合度:提高聚合度是保证高强度的首要条件,一般大分子聚合度越高,大分
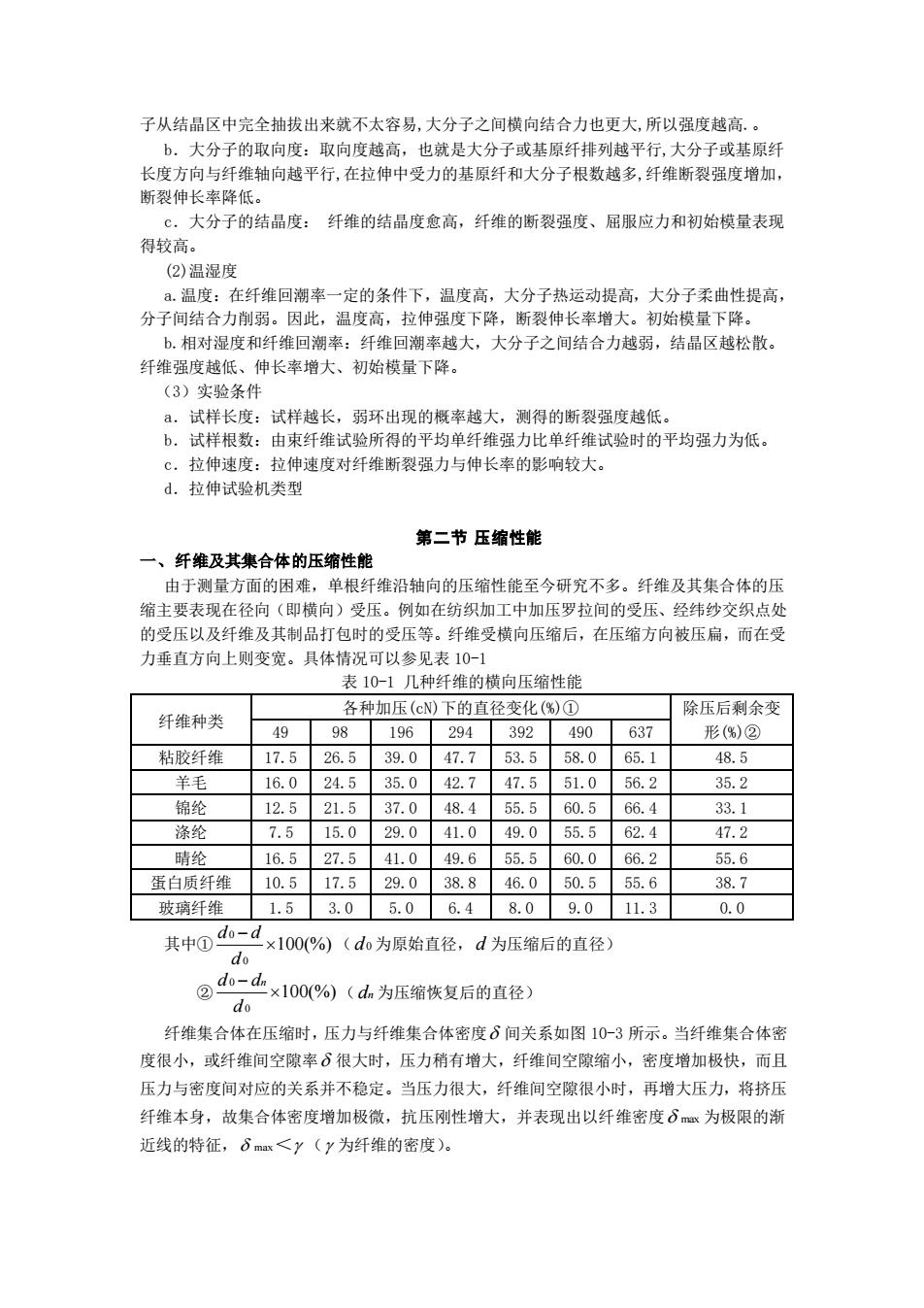
子从结晶区中完全抽拔出来就不太容易,大分子之间横向结合力也更大,所以强度越高。 大分子的取向度:取向度越高 也就是大分子或基原纤排列越平行,大分子或基原纤 长度方向与纤维轴向越平行,在拉伸中受力的基原纤和大分子根数越多,纤维断裂强度增加 断裂伸长率降低。 ℃,大分子的结品度:纤维的结晶度愈高,纤维的断裂强度、屈服应力和初始模量表现 得较高。 2)温湿度 .温度:在纤维回潮率一定的条件下,温度高,大分子热运动提高, 大分子柔曲性提高 分子间结合力削弱。因此,温度高,拉伸强度下降,断裂伸长率增大。初始模量下降。 b.相对湿度和纤维回潮率:纤维回海率越大,大分子之间结合力越弱,结晶区越松散。 纤维强度越低、伸长率增大、初始模量下降。 (3)实验条件 8 试样长度:试样越长,弱环出现的概率越大,测得的断裂强度越低 试样根数 由束纤维试验所得的平均单纤维强力比单纤维试验时的平均强力为低 C.拉伸速度:拉伸速度对纤维断裂强力与伸长率的影响较大。 d.拉伸试验机类型 第二节压缩性能 纤维及其集合体的压缩性能 由于测量方面的困难,单根纤维沿轴向的压缩性能至今研究不多。纤维及其集合体的压 缩主要表现在径向(即横向)受压。例如在纺织加工中加压罗拉间的受压、经纬纱交织点处 的受压以及纤维及其制品打包时的受压等。纤维受横向压缩后,在压缩方向被压扁,而在受 力垂直方向上则变宽。具体情况可以参见表10-1 表10-1几种纤维的横向压缩性能 各种加压(cN)下的直径变化(① 纤维种类 除压后剩余变 4998 196294 392 490637 形(%)② 粘胶纤维 17.526.539.047.753.558.065.1 48.5 16.024.5 35.042.747.5 51.056.2 35.2 锦纶 12,521.5 37.048.455.560.566.4 33.1 涤纶 7.5 15.0 29.041.049.055.562.4 47.2 睛纶 16.527.541.049.655.560.066.2 55.6 蛋白质纤维 10.5 17.5 29.0 38.8 46.0 50.555.6 38.7 玻璃纤维1.53.05.06.48.09.011.3 0.0 其中0o-d d。 100(%)(d0为原始直径,d为压缩后的直径) @d-4×1000%(d为压缩恢复后的直径) do 纤维集合体在压缩时,压力与纤维集合体密度6间关系如图10-3所示。当纤维集合体密 度很小,或纤维间空隙率很大时,压力稍有增大,纤维间空隙缩小,密度增加极快,而且 压力与密度间对应的关系并不稳定。当压力很大,纤维间空隙很小时,再增大压力,将挤压 纤维本身,故集合体密度增加极微,抗压刚性增大,并表现出以纤维密度δ为极限的 近线的特征,6<y(y为纤维的密度)
子从结晶区中完全抽拔出来就不太容易,大分子之间横向结合力也更大,所以强度越高.。 b.大分子的取向度:取向度越高,也就是大分子或基原纤排列越平行,大分子或基原纤 长度方向与纤维轴向越平行,在拉伸中受力的基原纤和大分子根数越多,纤维断裂强度增加, 断裂伸长率降低。 c.大分子的结晶度: 纤维的结晶度愈高,纤维的断裂强度、屈服应力和初始模量表现 得较高。 (2)温湿度 a.温度:在纤维回潮率一定的条件下,温度高,大分子热运动提高,大分子柔曲性提高, 分子间结合力削弱。因此,温度高,拉伸强度下降,断裂伸长率增大。初始模量下降。 b.相对湿度和纤维回潮率:纤维回潮率越大,大分子之间结合力越弱,结晶区越松散。 纤维强度越低、伸长率增大、初始模量下降。 (3)实验条件 a.试样长度:试样越长,弱环出现的概率越大,测得的断裂强度越低。 b.试样根数:由束纤维试验所得的平均单纤维强力比单纤维试验时的平均强力为低。 c.拉伸速度:拉伸速度对纤维断裂强力与伸长率的影响较大。 d.拉伸试验机类型 第二节 压缩性能 一、纤维及其集合体的压缩性能 由于测量方面的困难,单根纤维沿轴向的压缩性能至今研究不多。纤维及其集合体的压 缩主要表现在径向(即横向)受压。例如在纺织加工中加压罗拉间的受压、经纬纱交织点处 的受压以及纤维及其制品打包时的受压等。纤维受横向压缩后,在压缩方向被压扁,而在受 力垂直方向上则变宽。具体情况可以参见表 10-1 表 10-1 几种纤维的横向压缩性能 纤维种类 各种加压(cN)下的直径变化(%)① 除压后剩余变 49 98 196 294 392 490 637 形(%)② 粘胶纤维 17.5 26.5 39.0 47.7 53.5 58.0 65.1 48.5 羊毛 16.0 24.5 35.0 42.7 47.5 51.0 56.2 35.2 锦纶 12.5 21.5 37.0 48.4 55.5 60.5 66.4 33.1 涤纶 7.5 15.0 29.0 41.0 49.0 55.5 62.4 47.2 晴纶 16.5 27.5 41.0 49.6 55.5 60.0 66.2 55.6 蛋白质纤维 10.5 17.5 29.0 38.8 46.0 50.5 55.6 38.7 玻璃纤维 1.5 3.0 5.0 6.4 8.0 9.0 11.3 0.0 其中① 0 0 100(%) d d d − ( d0 为原始直径, d 为压缩后的直径) ② 0 0 100(%) d dn d − ( dn 为压缩恢复后的直径) 纤维集合体在压缩时,压力与纤维集合体密度 间关系如图 10-3 所示。当纤维集合体密 度很小,或纤维间空隙率 很大时,压力稍有增大,纤维间空隙缩小,密度增加极快,而且 压力与密度间对应的关系并不稳定。当压力很大,纤维间空隙很小时,再增大压力,将挤压 纤维本身,故集合体密度增加极微,抗压刚性增大,并表现出以纤维密度 max 为极限的渐 近线的特征, max< ( 为纤维的密度)
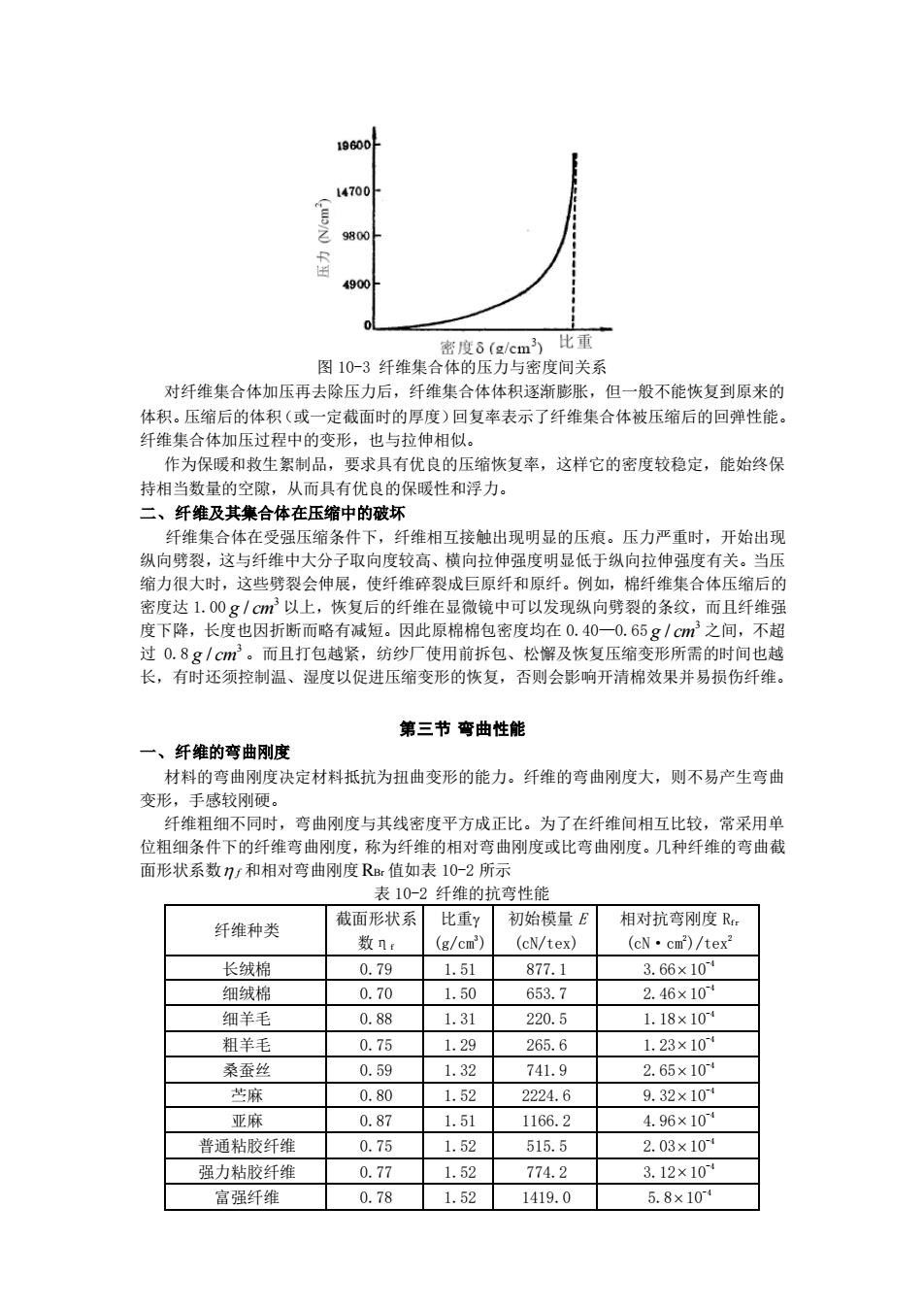
14700 9800 0 度8(g/cm 比而 图10-3纤维集合体的压力与密度间关系 对纤维集合体加压再去除压力后,纤维集合体体积逐渐膨胀,但一般不能恢复到原来的 体积。压缩后的体积(或一定截面时的厚度)回复率表示了纤维集合体被压缩后的回弹性能, 纤维集合体士 压过程中的变形,也与拉伸相似 作为保暖和救生絮制品,要求具有优良的压缩恢复率,这样它的密度较稳定,能始终保 持相当数量的空隙,从而具有优良的保暖性和浮力。 二、纤维及其集合体在压缩中的破坏 纤维集合体在受强压缩条件下,纤维相互接触出现明显的压痕。压力严重时,开始出现 纵向裂这与红维中大分子取向度高、墙向拉伸度明低纵向拉伸强度右关。当压 纤维碎裂成巨原纤和原纤。 上 恢复 的纤 2微镜中 向劈 的条纹 而且纤维 度下降,长度也因折断而略有减短 因此原棉棉包密度均在0.40一0.65g/cm之间,不起 过0.8g/cm。而且打包越紧,纺纱厂使用前拆包、松懈及恢复压缩变形所需的时间也越 长,有时还须控制温、湿度以促进压缩变形的恢复,否则会影响开清棉效果并易损伤纤维。 第三节弯曲性能 一、纤维的弯曲刚度 材料的弯曲刚度决定材料抵抗为扭曲变形的能力。纤维的弯曲刚度大,则不易产生弯曲 变形,手感较刚硬。 纤维粗细不同时,弯曲刚度与其线密度平方成正比。为了在纤维间相互比较,常采用单 位粗细条件下的纤维弯曲刚度,称为纤维的相对弯曲刚度或比弯曲刚度。几种纤维的弯曲截 面形状系数/和相对湾曲刚度R值如表10-2所示 表10-2纤维的抗弯性 纤维种类 截面形状系 比重y 初始模量 相对抗弯刚度R: 数n, (g/cm) (cN/tex) (cN·cm/texi 长绒棉 0.79 1.51 8771 3.66×10 细绒棉 070 1.50 6537 246×10 细羊毛 0.88 1.31 220.5 L18×10 粗单手 0.75 1.29 265.6 1.23×10 秀香独 0.59 1.32 741.9 2.65×104 0.80 1.52 2224.6 9.32×10 亚麻 0.87 1.51 1166.2 4.96×10 普通钻胶纤雄 075 152 515.5 2.03×10-t 强力粘胶纤维 0.77 1.52 774.2 3.12×10 富强纤维 0.78 1.52 1419.0 5.8×10
图 10-3 纤维集合体的压力与密度间关系 对纤维集合体加压再去除压力后,纤维集合体体积逐渐膨胀,但一般不能恢复到原来的 体积。压缩后的体积(或一定截面时的厚度)回复率表示了纤维集合体被压缩后的回弹性能。 纤维集合体加压过程中的变形,也与拉伸相似。 作为保暖和救生絮制品,要求具有优良的压缩恢复率,这样它的密度较稳定,能始终保 持相当数量的空隙,从而具有优良的保暖性和浮力。 二、纤维及其集合体在压缩中的破坏 纤维集合体在受强压缩条件下,纤维相互接触出现明显的压痕。压力严重时,开始出现 纵向劈裂,这与纤维中大分子取向度较高、横向拉伸强度明显低于纵向拉伸强度有关。当压 缩力很大时,这些劈裂会伸展,使纤维碎裂成巨原纤和原纤。例如,棉纤维集合体压缩后的 密度达 1.00 3 g cm / 以上,恢复后的纤维在显微镜中可以发现纵向劈裂的条纹,而且纤维强 度下降,长度也因折断而略有减短。因此原棉棉包密度均在 0.40—0.65 3 g cm / 之间,不超 过 0.8 3 g cm / 。而且打包越紧,纺纱厂使用前拆包、松懈及恢复压缩变形所需的时间也越 长,有时还须控制温、湿度以促进压缩变形的恢复,否则会影响开清棉效果并易损伤纤维。 第三节 弯曲性能 一、纤维的弯曲刚度 材料的弯曲刚度决定材料抵抗为扭曲变形的能力。纤维的弯曲刚度大,则不易产生弯曲 变形,手感较刚硬。 纤维粗细不同时,弯曲刚度与其线密度平方成正比。为了在纤维间相互比较,常采用单 位粗细条件下的纤维弯曲刚度,称为纤维的相对弯曲刚度或比弯曲刚度。几种纤维的弯曲截 面形状系数 f 和相对弯曲刚度 RBr 值如表 10-2 所示 表 10-2 纤维的抗弯性能 纤维种类 截面形状系 数ηf 比重 (g/cm3 ) 初始模量 E (cN/tex) 相对抗弯刚度 Rfr (cN·cm2 )/tex2 长绒棉 0.79 1.51 877.1 3.66 10-4 细绒棉 0.70 1.50 653.7 2.46 10-4 细羊毛 0.88 1.31 220.5 1.18 10-4 粗羊毛 0.75 1.29 265.6 1.23 10-4 桑蚕丝 0.59 1.32 741.9 2.65 10-4 苎麻 0.80 1.52 2224.6 9.32 10-4 亚麻 0.87 1.51 1166.2 4.96 10-4 普通粘胶纤维 0.75 1.52 515.5 2.03 10-4 强力粘胶纤维 0.77 1.52 774.2 3.12 10-4 富强纤维 0.78 1.52 1419.0 5.8 10-4
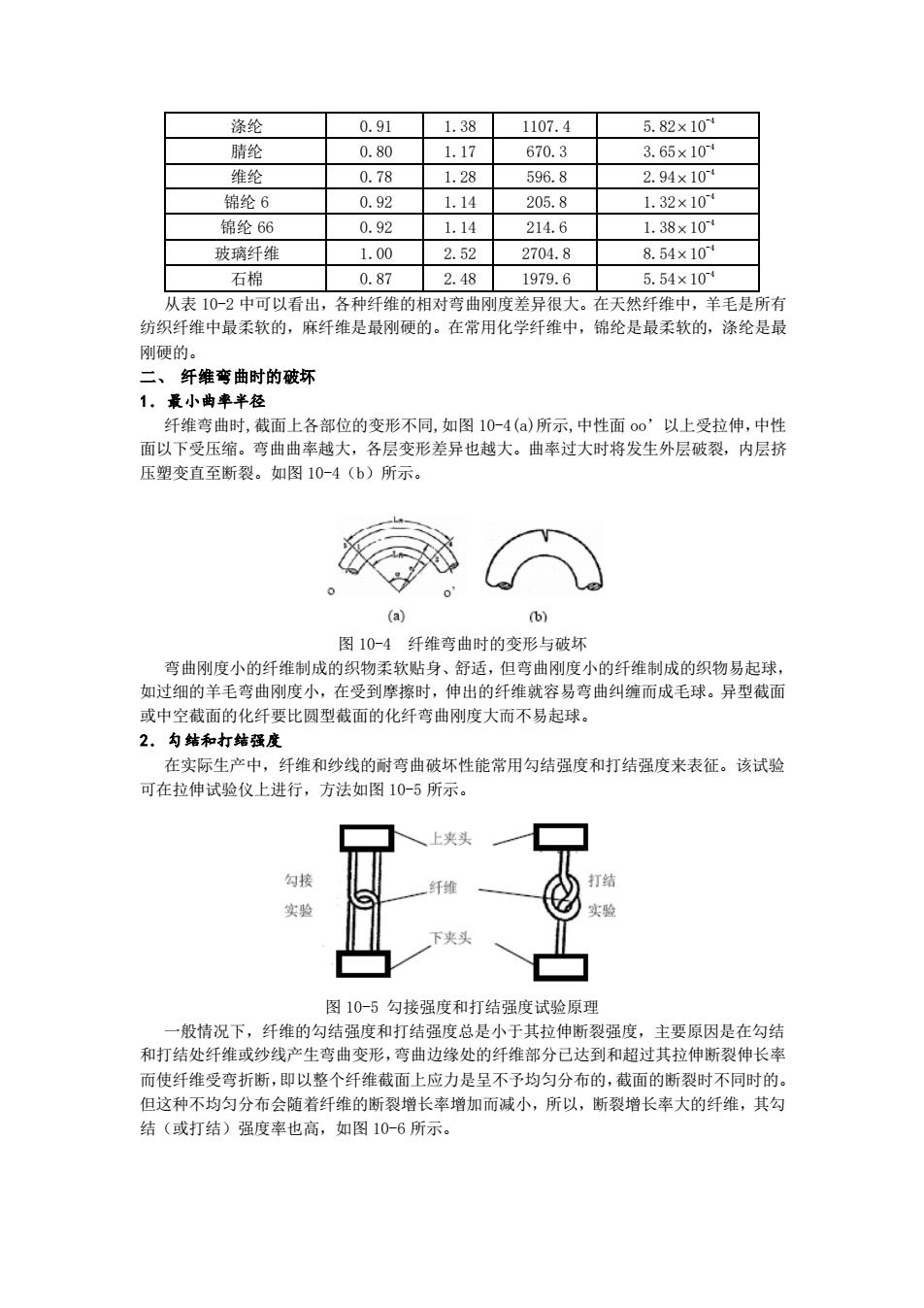
涤纶 091 1.381107.4 5.82×101 腈纶 0.80 1.17 670.3 365×10 维纶 0.78 1.28 596.8 2.94×10 锦纶6 092 114 2058 139×104 锦纶66 0.92 1.14 214.6 1.38×10 玻璃纤维 1.00 2.52 2704.8 8.54×10 石棉 0.87 2481q796 5.54×104 表10-2中可可以看出 冬种红维的相对曲风府差异很大。在天姚红维中,羊毛是所 纺织纤维中最柔软的 千维是最刚硬的 在常用 纶是最柔软的, 涤纶是最 列硬的 二、纤维膏曲时的破环 1.最小曲率半径 纤维弯曲时截面上各部位的变形不同.如图10-4(a)所示中性面00'以上号拉伸,中性 面以下受压缩。弯曲曲率越大,各层变形差异也越大。曲率过大时将发生外层破裂,内层 压塑变直至断裂 如图10-4(b)所示 (b) 图10-4纤维弯曲时的变形与破坏 弯曲刚度小的纤维制成的织物柔软贴身、舒适,但弯曲刚度小的纤维制成的织物易起球, 如过细的羊毛弯曲刚度小,在受到摩擦时,伸出的纤维就容易弯曲纠缠而成毛球。异型截面 或中空截面的化纤要比圆型截面的化纤弯曲刚度大而不易起球。 2.勾结和打结强度 在实际生产中,纤维和纱线的耐弯曲破坏性能常用勾结强度和打结强度米表征。该试验 可在拉伸试验仪上进行,方法如图10-5所示 上夹头 图10-5勾接强度和打结强度试验原理 ~般情况下,纤维的勾结强度和打结强度总是小于其拉伸断裂强度,主要原因是在勾结 和打结处纤维或纱线产生弯曲变形,弯曲边缘处的纤维部分已达到和超过其拉伸断裂伸长率 而使纤雄受弯折断,即以整个纤维截面上应力是县不子均匀分布的,截面的断列时不同时的 但这种不均匀分布会随若纤维的断裂增长率增加而减小,所以,断裂增长率大的纤维,其公 结(或打结)强度率也高,如图10-6所示
涤纶 0.91 1.38 1107.4 5.82 10-4 腈纶 0.80 1.17 670.3 3.65 10-4 维纶 0.78 1.28 596.8 2.94 10-4 锦纶 6 0.92 1.14 205.8 1.32 10-4 锦纶 66 0.92 1.14 214.6 1.38 10-4 玻璃纤维 1.00 2.52 2704.8 8.54 10-4 石棉 0.87 2.48 1979.6 5.54 10-4 从表 10-2 中可以看出,各种纤维的相对弯曲刚度差异很大。在天然纤维中,羊毛是所有 纺织纤维中最柔软的,麻纤维是最刚硬的。在常用化学纤维中,锦纶是最柔软的,涤纶是最 刚硬的。 二、 纤维弯曲时的破坏 1.最小曲率半径 纤维弯曲时,截面上各部位的变形不同,如图 10-4(a)所示,中性面 oo’以上受拉伸,中性 面以下受压缩。弯曲曲率越大,各层变形差异也越大。曲率过大时将发生外层破裂,内层挤 压塑变直至断裂。如图 10-4(b)所示。 图 10-4 纤维弯曲时的变形与破坏 弯曲刚度小的纤维制成的织物柔软贴身、舒适,但弯曲刚度小的纤维制成的织物易起球, 如过细的羊毛弯曲刚度小,在受到摩擦时,伸出的纤维就容易弯曲纠缠而成毛球。异型截面 或中空截面的化纤要比圆型截面的化纤弯曲刚度大而不易起球。 2.勾结和打结强度 在实际生产中,纤维和纱线的耐弯曲破坏性能常用勾结强度和打结强度来表征。该试验 可在拉伸试验仪上进行,方法如图 10-5 所示。 图 10-5 勾接强度和打结强度试验原理 一般情况下,纤维的勾结强度和打结强度总是小于其拉伸断裂强度,主要原因是在勾结 和打结处纤维或纱线产生弯曲变形,弯曲边缘处的纤维部分已达到和超过其拉伸断裂伸长率 而使纤维受弯折断,即以整个纤维截面上应力是呈不予均匀分布的,截面的断裂时不同时的。 但这种不均匀分布会随着纤维的断裂增长率增加而减小,所以,断裂增长率大的纤维,其勾 结(或打结)强度率也高,如图 10-6 所示

°% d中 图10-6不同断裂增长率纤维的勾结强度率 第四节势切性能 一、纤维的抗扭刚度 纤维与任何物体一样,在受到扭矩作用下,都会产生扭变形,如图10-7所示。当一个圆 柱体在扭矩T作用下,上端面对下端面产生扭变形时,则 0= TI 式中:0扭变形角(弧度) T-扭矩(cN.cm) 1-长度(cm) E,.前切弹性模量(cN/cm2) b-截面的极断面惯性矩(cm4) 图10-7扭变形示意图 二、纤维扭转时的破环 随着扭转变形的增大,纤维中的剪切应力增大,造成结晶区的破碎和非晶区中大分子链 被拉断,沿纵向碎裂,最后断裂破坏。一般来说,纤维的剪切强度小于拉伸强度。 当扭转变形达到一定程度时,沿纤维纵向的剪切可能使纤维劈裂开来,进一步发展,纤 维随之解体或断裂。表示纤维抵抗扭转破坏能力的指标是捻断纤维时的加艳角(外层螺旋角 a),见表10-3所示 表10-3各种纤维的断裂捻角 纤维 断裂捻角α(度) 种类 短纤维长丝
断裂伸长率 (%) 纤维勾接强度 (%) 图 10-6 不同断裂增长率纤维的勾结强度率 第四节 剪切性能 一、纤维的抗扭刚度 纤维与任何物体一样,在受到扭矩作用下,都会产生扭变形,如图 10-7 所示。当一个圆 柱体在扭矩 T 作用下,上端面对下端面产生扭变形时,则 . t p . T l E I = 式中: -扭变形角(弧度) T -扭矩(cN.cm) l -长度(cm) Et -剪切弹性模量(cN/cm2) Ip -截面的极断面惯性矩(cm4) T l r 图 10-7 扭变形示意图 二、纤维扭转时的破坏 随着扭转变形的增大,纤维中的剪切应力增大,造成结晶区的破碎和非晶区中大分子链 被拉断,沿纵向碎裂,最后断裂破坏。一般来说,纤维的剪切强度小于拉伸强度。 当扭转变形达到一定程度时,沿纤维纵向的剪切可能使纤维劈裂开来,进一步发展,纤 维随之解体或断裂。表示纤维抵抗扭转破坏能力的指标是捻断纤维时的加捻角(外层螺旋角 ),见表 10-3 所示。 表 10-3 各种纤维的断裂捻角 纤维 种类 断裂捻角 (度) 短纤维 长丝

棉 34^37 单毛 38.541.5 蚕丝 39 亚麻 21.529.5 普通粘胶 35.539.5 355*39.5 强力粘胶 31.533.5 31.533.5 铜氨纤维 4042 33.535 醋酯纤维 40.5>46 40.546 涤纶 59 4250 锦纶 5663 47.555.5 腈纶 33^34.5 酪素纤维 58.5^62 玻璃纤维 2.5^5 第五节表面摩擦与抱合性质 一、纤维摩擦抱合性能的基本特征 当相互接触的纤维或使纤维与其他材料在法向压力下沿接触面相互滑移时,在接触面间 将会产生阻碍这一滑移的切向阻力,该阻力与所加法向压力成正比。对一般材料,法向压力 为零,该切向阻力亦为零。但是纺织材料在法向压力为零时,切向阻力并不为零,这因为纷 织纤维细软而多转曲,并有较好的弹性。当相互接触的不是纤维而使纤维集合体时,因为形 成接触界面的依然是纤维,因此,上述特征仍然存在。 按此分析,这是在纤维接触截面处产生的切向阻力下应由两部分组成,即法向压力为零 时的切向阻力和因法向压力而引起的切向阻力,前者称为抱合力(或集束力)F,后者称为 摩擦力E 定义切向阻力与接触面上法向压力N之比为切向阻抗系数,即: 因为只有摩擦力和法向压力N有关,因此,上式又可改写为: 二、纤维摩擦性能的形成机理 用于说明纤维间摩擦力的理论有多种,但鉴于纤维材料是一种表面不平整度较高、可塑 性较强的高分子材料,因此,目前均倾向于用“焊接”的观点来说明它的形成原理。 该观点认为摩擦力来自存在于两物体间真正接触点的实际联结(或称“焊接”)。在滑动 开始时,为剪切开这些焊接点所需克服的阻力即为摩擦力。因为该理论认为大多数材料的表 面都是不规则的,在他们互相接触时,最初也只在少数粗糙的顶尖处才产生真正的接触,因 此加在这几个真正接触点上的负荷就有可能形成很大的压力,使接触点处的材料屈服流动, 并随着流动的进行,两物体间的接触面不断增大。这一过程一直要进行到增加后的接触面积 能使整个接触点间的压力降到足以承受所加负荷的屈服应力时为止,但这实在接触点周围的 邻近区域里仍然保留若弹性变形。 设A为因屈服流动而形成的真正接触面积,则有:
棉 34~37 — 羊毛 38.5~41.5 — 蚕丝 — 39 亚麻 21.5~29.5 — 普通粘胶 35.5~39.5 35.5~39.5 强力粘胶 31.5~33.5 31.5~33.5 铜氨纤维 40~42 33.5~35 醋酯纤维 40.5~46 40.5~46 涤纶 59 42~50 锦纶 56~63 47.5~55.5 腈纶 33~34.5 — 酪素纤维 58.5~62 — 玻璃纤维 — 2.5~5 第五节 表面摩擦与抱合性质 一、纤维摩擦抱合性能的基本特征 当相互接触的纤维或使纤维与其他材料在法向压力下沿接触面相互滑移时,在接触面间 将会产生阻碍这一滑移的切向阻力,该阻力与所加法向压力成正比。对一般材料,法向压力 为零,该切向阻力亦为零。但是纺织材料在法向压力为零时,切向阻力并不为零,这因为纺 织纤维细软而多转曲,并有较好的弹性。当相互接触的不是纤维而使纤维集合体时,因为形 成接触界面的依然是纤维,因此,上述特征仍然存在。 按此分析,这是在纤维接触截面处产生的切向阻力 F 应由两部分组成,即法向压力为零 时的切向阻力和因法向压力而引起的切向阻力,前者称为抱合力(或集束力)F1,后者称为 摩擦力 F2。 定义切向阻力与接触面上法向压力 N 之比为切向阻抗系数 ,即: F N = 因为只有摩擦力和法向压力 N 有关,因此,上式又可改写为: F1 f N = + 二、纤维摩擦性能的形成机理 用于说明纤维间摩擦力的理论有多种,但鉴于纤维材料是一种表面不平整度较高、可塑 性较强的高分子材料,因此,目前均倾向于用“焊接”的观点来说明它的形成原理。 该观点认为摩擦力来自存在于两物体间真正接触点的实际联结(或称“焊接”)。在滑动 开始时,为剪切开这些焊接点所需克服的阻力即为摩擦力。因为该理论认为大多数材料的表 面都是不规则的,在他们互相接触时,最初也只在少数粗糙的顶尖处才产生真正的接触,因 此加在这几个真正接触点上的负荷就有可能形成很大的压力,使接触点处的材料屈服流动, 并随着流动的进行,两物体间的接触面不断增大。这一过程一直要进行到增加后的接触面积 能使整个接触点间的压力降到足以承受所加负荷的屈服应力时为止,但这实在接触点周围的 邻近区域里仍然保留着弹性变形。 设 A 为因屈服流动而形成的真正接触面积,则有:
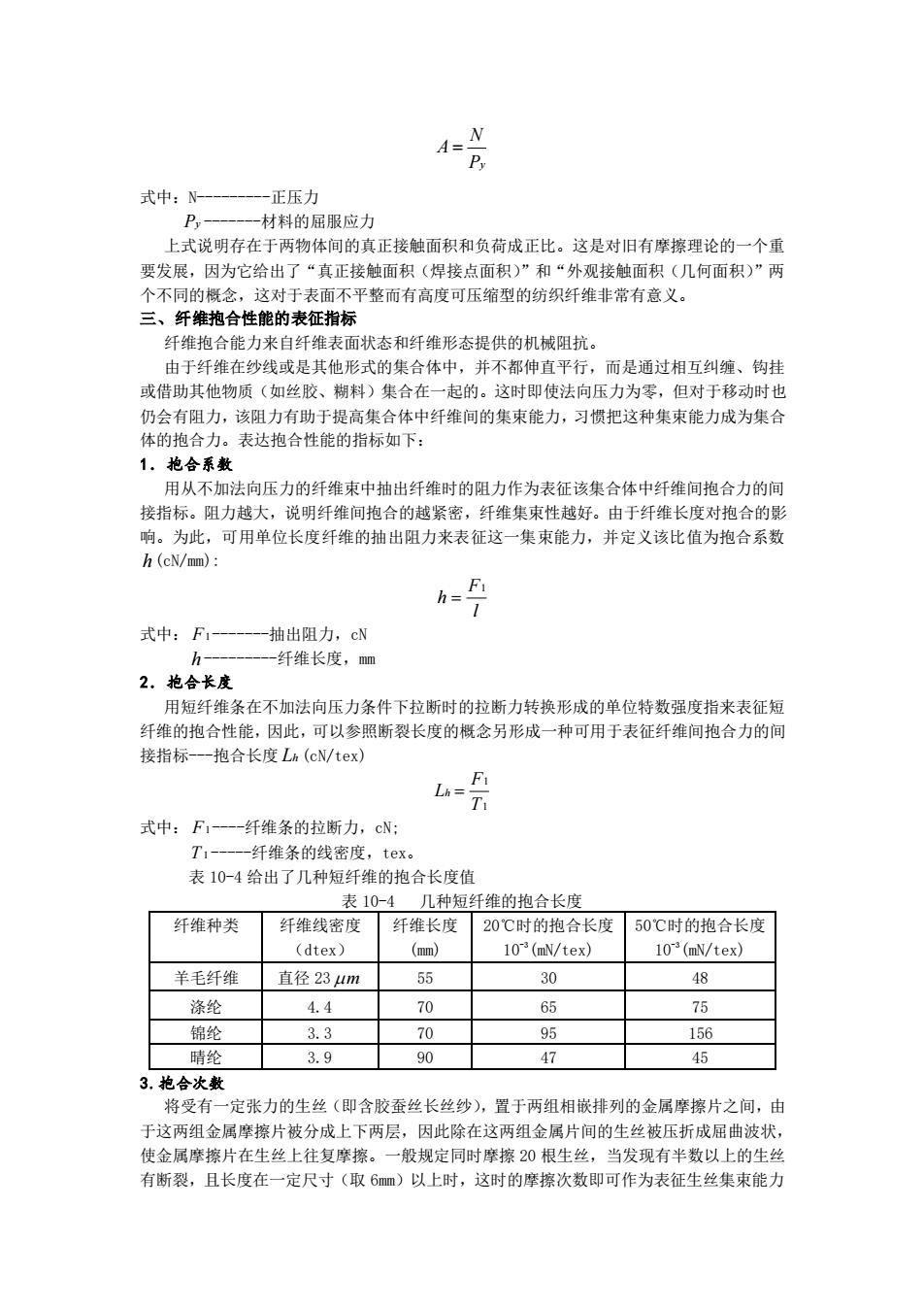
A=N 式中: 正压力 材料的屈服应力 上式说明存在于两物体间的真正接触面积和负荷成正比。这是对旧有摩擦理论的一个重 要发展,因为它给出了“真正接触面积(焊接点面积)”和“外观接触面积(几何面积)”两 个不同的概今这对面 平整而有高度可压缩型的纺织纤维非常有意义。 三、纤维抱合性能的表征指 纤维抱合能力来自纤维表面状态和纤维形态提供的机械阻抗。 由于纤维在纱线或是其他形式的集合体中,并不都伸直平行,而是通过相互纠缠、钩挂 或借助其他物质(如丝胶、糊料)集合在一起的。这时即使法向压力为零,但对于移动时也 仍会有阻力,该阻力有助于提高集合体中纤维间的集束能力,习惯把这种集束能力成为集合 体的抱合力表达抱合性能的指标如下 1,抱合系数 用从不加法向压力的纤维束中抽出纤维时的阻力作为表征该集合体中纤维间抱合力的间 接指标。阻力越大,说明纤维间抱合的越紧密,纤维集束性越好。由于纤维长度对抱合的影 响。为此,可用单位长度纤维的抽出阻力来表征这一集束能力,并定义该比值为抱合系数 h(cN/mm): h 式中:F -抽出阻力.cN 一纤维长度,m 2.地合长度 用短纤维条在不加法向压力条件下拉断时的拉断力转换形成的单位特数强度指来表征短 纤维的抱合性能,因此,可以参照断裂长度的概念另形成一种可用于表征纤维间抱合力的间 接指标-一抱合长度Lh(cN/tex) 式中:F 纤维条的拉断力,cN: 111 纤维条的线密度,tex。 表10-4给出了几种短纤维的抱合长度值 表10-4几种短纤维的抱合长度 纤维种类 纤维线密度 纤维长府 20C时的抱合长度50℃时的抱合长府 (dtex) 10(mN/tex 10(mN/tex) 羊毛纤维 直径234m 55 30 48 涤纶 4.4 70 75 锦纶 3.3 70 95 156 睹纶 3.9 90 47 45 3.抱合次数 将受 定张力的生丝(即含胶蚕丝长丝纱),置于两组相嵌排列的金属摩擦片之间,由 于这两组金属摩擦片被分成上下两层,因此除在这两组金属片间的生丝被压折成届曲波状 使金属摩擦片在生丝上往复摩擦。一般规定同时摩擦20根生丝,当发现有半数以上的生丝 有断裂,且长度在一定尺十(取6mm)以上时,这时的摩擦次数即可作为表征生丝集束能力
y N A P = 式中:N-正压力 Py -材料的屈服应力 上式说明存在于两物体间的真正接触面积和负荷成正比。这是对旧有摩擦理论的一个重 要发展,因为它给出了“真正接触面积(焊接点面积)”和“外观接触面积(几何面积)”两 个不同的概念,这对于表面不平整而有高度可压缩型的纺织纤维非常有意义。 三、纤维抱合性能的表征指标 纤维抱合能力来自纤维表面状态和纤维形态提供的机械阻抗。 由于纤维在纱线或是其他形式的集合体中,并不都伸直平行,而是通过相互纠缠、钩挂 或借助其他物质(如丝胶、糊料)集合在一起的。这时即使法向压力为零,但对于移动时也 仍会有阻力,该阻力有助于提高集合体中纤维间的集束能力,习惯把这种集束能力成为集合 体的抱合力。表达抱合性能的指标如下: 1.抱合系数 用从不加法向压力的纤维束中抽出纤维时的阻力作为表征该集合体中纤维间抱合力的间 接指标。阻力越大,说明纤维间抱合的越紧密,纤维集束性越好。由于纤维长度对抱合的影 响。为此,可用单位长度纤维的抽出阻力来表征这一集束能力,并定义该比值为抱合系数 h (cN/mm): F1 h l = 式中: F1 -抽出阻力,cN h -纤维长度,mm 2.抱合长度 用短纤维条在不加法向压力条件下拉断时的拉断力转换形成的单位特数强度指来表征短 纤维的抱合性能,因此,可以参照断裂长度的概念另形成一种可用于表征纤维间抱合力的间 接指标-抱合长度 Lh (cN/tex) 1 1 h F L T = 式中: F1 -纤维条的拉断力,cN; T1 -纤维条的线密度,tex。 表 10-4 给出了几种短纤维的抱合长度值 表 10-4 几种短纤维的抱合长度 纤维种类 纤维线密度 (dtex) 纤维长度 (mm) 20℃时的抱合长度 10-3 (mN/tex) 50℃时的抱合长度 10-3 (mN/tex) 羊毛纤维 直径 23 m 55 30 48 涤纶 4.4 70 65 75 锦纶 3.3 70 95 156 晴纶 3.9 90 47 45 3.抱合次数 将受有一定张力的生丝(即含胶蚕丝长丝纱),置于两组相嵌排列的金属摩擦片之间,由 于这两组金属摩擦片被分成上下两层,因此除在这两组金属片间的生丝被压折成屈曲波状, 使金属摩擦片在生丝上往复摩擦。一般规定同时摩擦 20 根生丝,当发现有半数以上的生丝 有断裂,且长度在一定尺寸(取 6mm)以上时,这时的摩擦次数即可作为表征生丝集束能力

的指标,称为抱合次数。 第六节疲劳性质 一、应力松驰和塌变的基本橛念 1.定义 应力松弛:纤维在拉伸变形恒定条件下,应力随时间的延长而逐渐减小的现象称为应力 松弛 媚变:纤维在一恒定拉伸外力作用下,变形随受力时间的延长而逐渐增加的现象称为蠕 变。 2.三种形变 如纤维的蠕变恢复曲线图108所示,伸直变形可以分为三种,三部分变形的比例由纤 维的内部结构决定。 急弹性变形: 一部分变形是在外力作用下,纤维大分子主链的键长和键角增加以及分 子键之间次价键的伸长,且伸长变形与外力成正比,伸长或恢复的速率与原子的热振动速 奉相当,可以看作是瞬时的,即E和E3。 缓弹性变形:第二部分变形是外力作用下,非结晶区中一部分分子链段从卷曲状态沿力 场方向伸展,这时必须克服分子间或分子内的各种远程或进程的次价键力,变形过程比较 缓慢。当外力去除后,伸展的大分子间又通过键节的热运动而重新取得卷曲构象的趋向 这一过程同样需要克服各种远程和近程的次价键力, 该过程需要时间。这部分随时间而逐 步伸长或恢复的变形成为缓弹性变形62和54。 图10-8纤维的蜡变及错变回复曲线 塑性变形:第三部分变形是外力作用下 大分子链间产生不可逆的位移,即分子链在克 服次价键力后伸长或分子链间相互滑动,在新的状态下重新建立较强的次价健,使分子链 节的热运动不可能克服新的次价键力而回复,即产生了塑性变形5。 二、纤维的赚性 纤维弹性是指纤维变性的回复能力,又称弹性回复性能或回弹性。 弹性的指标 表不 纤维弹性的常用指标是弹性回复率e。它是指急弹性变形3(≈8)和一定时间 内的缓弹性变形64占总变形江的百分率,即:
的指标,称为抱合次数。 第六节 疲劳性质 一、应力松弛和蠕变的基本概念 1.定义 应力松弛:纤维在拉伸变形恒定条件下,应力随时间的延长而逐渐减小的现象称为应力 松弛。 蠕变:纤维在一恒定拉伸外力作用下,变形随受力时间的延长而逐渐增加的现象称为蠕 变。 2.三种形变 如纤维的蠕变恢复曲线图 10-8 所示,伸直变形可以分为三种,三部分变形的比例由纤 维的内部结构决定。 急弹性变形:第一部分变形是在外力作用下,纤维大分子主链的键长和键角增加以及分 子键之间次价键的伸长,且伸长变形与外力成正比,伸长或恢复的速率与原子的热振动速 率相当,可以看作是瞬时的,即 1 3 和 。 缓弹性变形:第二部分变形是外力作用下,非结晶区中一部分分子链段从卷曲状态沿力 场方向伸展,这时必须克服分子间或分子内的各种远程或进程的次价键力,变形过程比较 缓慢。当外力去除后,伸展的大分子间又通过键节的热运动而重新取得卷曲构象的趋向, 这一过程同样需要克服各种远程和近程的次价键力,该过程需要时间。这部分随时间而逐 步伸长或恢复的变形成为缓弹性变形 2 4 和 。 P0 31 P 1 2 4 5 3 t t t1 t2 t O O t1 t2 图 10-8 纤维的蠕变及蠕变回复曲线 塑性变形:第三部分变形是外力作用下,大分子链间产生不可逆的位移,即分子链在克 服次价键力后伸长或分子链间相互滑动,在新的状态下重新建立较强的次价键,使分子链 节的热运动不可能克服新的次价键力而回复,即产生了塑性变形 5 。 二、纤维的弹性 纤维弹性是指纤维变性的回复能力,又称弹性回复性能或回弹性。 1.弹性的指标 表示纤维弹性的常用指标是弹性回复率 e 。它是指急弹性变形 3 ( 1 )和一定时间 内的缓弹性变形 4 占总变形 T 的百分率,即: