
華柬师免大學|数学科学学院 School of Mathematical Sciences.East China Normal University 矩阵向量乘积 并行算法 (OpenMP) http://math.ecnu.edu.cn/~jypan
http://math.ecnu.edu.cn/~jypan 矩阵向量乘积 并行算法 (OpenMP)

华东师范大学数学科学学院 目录页 School of Mathematical Sciences,ECNU Contents 1 并行计算预备知识 2 矩阵向量并行乘积 http://math.ecnu.edu.cn/~jypan
http://math.ecnu.edu.cn/~jypan 目录页 Contents 华东师范大学 数学科学学院 School of Mathematical Sciences, ECNU http://math.ecnu.edu.cn/~jypan 1 2 并行计算预备知识 矩阵向量并行乘积

华东师范大学数学科学学院 目录页 School of Mathematical Sciences,ECNU Contents 预备知识 ■ 加速比与并行效率 性能优化 一些记号和设定 http://math.ecnu.edu.cn/~jypan
http://math.ecnu.edu.cn/~jypan 目录页 Contents 华东师范大学 数学科学学院 School of Mathematical Sciences, ECNU http://math.ecnu.edu.cn/~jypan 加速比与并行效率 性能优化 一些记号和设定 1 预备知识

并行算法基础知识 ●加速比 Ts Sp(q)= Tp(q) 其中T,串行程序执行时间,T,()为q个进程(线程)的执行时间 ·并行效率 Ep(q)= Sp(q) q http://math.ecnu.edu.cn/-jypan 4
http://math.ecnu.edu.cn/~jypan 4 并行算法基础知识 加速比 其中 Ts 串行程序执行时间,Tp(q) 为 q 个进程(线程)的执行时间 并行效率

程序性能优化 ■ 串行程序性能优化一并行程序性能优化的基础 ●调用高性能库。如:BLAS、LAPACK、FFTW ●选择编译器优化选项:-O2、-O3 ●合理定义数组维数 ●注意嵌套循环次数:数据访问的空间局部性和时间局部性 ●循环展开 ●数据分块 http://math.ecnu.edu.cn/-jypan 5
http://math.ecnu.edu.cn/~jypan 5 程序性能优化 串行程序性能优化 —并行程序性能优化的基础 调用高性能库。如:BLAS、LAPACK、FFTW 选择编译器优化选项:-O2、-O3 合理定义数组维数 注意嵌套循环次数:数据访问的空间局部性和时间局部性 数据分块 循环展开

程序性能优化 ■并行程序性能优化 ●负载平衡,减少进程(线程)的空闲时间 ·减少数据竞争 ●设计好的并行算法和通信模式 ●减少通信次数、提高通信粒度 ●多进程通信时尽量使用高效率的聚合通信算法 ●通信与计算的重叠 ·通过引入重复计算来减少通信 http://math.ecnu.edu.cn/-jypan 6
http://math.ecnu.edu.cn/~jypan 6 程序性能优化 并行程序性能优化 负载平衡,减少进程(线程)的空闲时间 减少数据竞争 设计好的并行算法和通信模式 减少通信次数、提高通信粒度 多进程通信时尽量使用高效率的聚合通信算法 通信与计算的重叠 通过引入重复计算来减少通信

华东师范大学数学科学学院 目录页 School of Mathematical Sciences,ECNU Contents 2 矩阵向量并行乘积 串行算法 自动并行 手动并行 http://math.ecnu.edu.cn/~jypan
http://math.ecnu.edu.cn/~jypan 目录页 Contents 华东师范大学 数学科学学院 School of Mathematical Sciences, ECNU http://math.ecnu.edu.cn/~jypan 串行算法 自动并行 手动并行 2 矩阵向量并行乘积
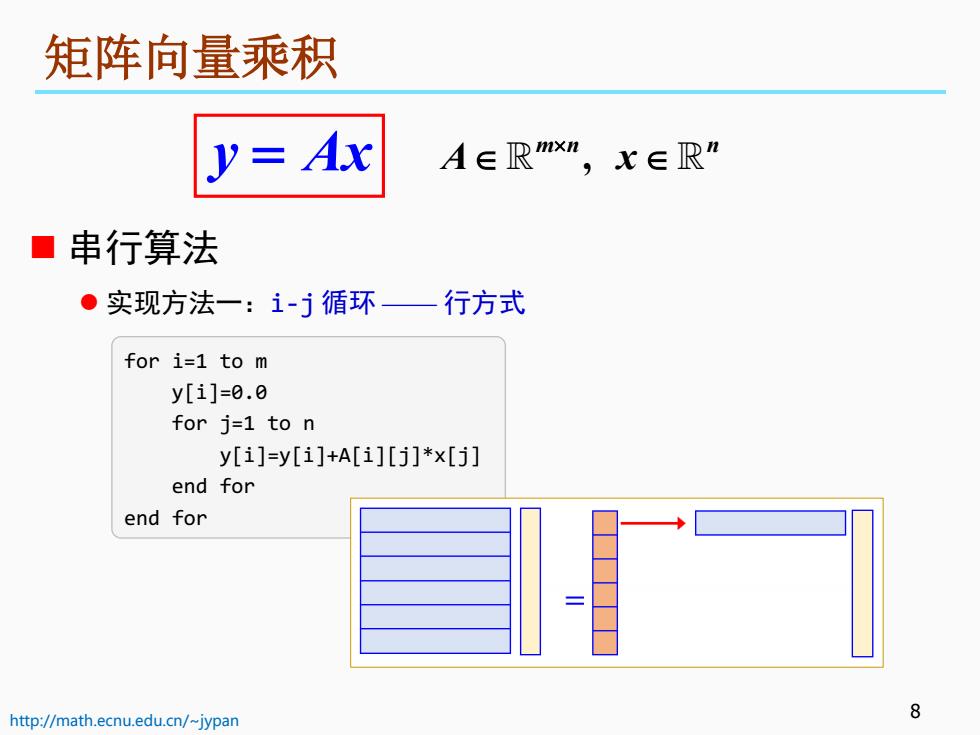
矩阵向量乘积 Ax y A∈Rmx”,x∈R” ·串行算法 ●实现方法一:i-j循环—行方式 for i=1 to m y[i]=8.0 for j=1 to n y[i]=y[i]+A[i][j]*x[j] end for end for http://math.ecnu.edu.cn/-jypan 8
http://math.ecnu.edu.cn/~jypan 8 矩阵向量乘积 串行算法 实现方法一:i-j 循环 —— 行方式 y Ax = , m n n A x × ∈ ∈ for i=1 to m y[i]=0.0 for j=1 to n y[i]=y[i]+A[i][j]*x[j] end for end for

矩阵向量乘积 ●实现方法二:j-i循环一列方式 /需先赋y初值.9 for j=1 to n for i=1 to m y[i]=y[i]+A[i][j]*x[j] end for end for C_MatVec.c 例:分别用两种方式计算y=Ax,其中A和x的元素为[O,1]中的随机小数, m,n取8192,输出两种方法所需的时间。 http://math.ecnu.edu.cn/-jypan 9
http://math.ecnu.edu.cn/~jypan 9 矩阵向量乘积 实现方法二:j-i 循环 — 列方式 // 需先赋 y 初值 0.0 for j=1 to n for i=1 to m y[i]=y[i]+A[i][j]*x[j] end for end for 例:分别用两种方式计算 y=Ax,其中 A 和 x 的元素为 [0,1] 中的随机小数, m, n 取 8192,输出两种方法所需的时间。 C_MatVec.c

矩阵向量并行乘积 ■并行算法一 ●自动并行:for循环共享 OMP_MatVec_for.c double A[m][n],x[n],y[m]; #pragma omp parallel for shared(A,x,y2)private(j) for(i=0;i<m;i++) y2[i]=0.0; for(j=0;j<n;j++) y2[i]+=A[i][]*x[j]; http://math.ecnu.edu.cn/-jypan 10
http://math.ecnu.edu.cn/~jypan 10 矩阵向量并行乘积 并行算法一 自动并行:for 循环共享 double A[m][n], x[n], y[m]; ... ... #pragma omp parallel for shared(A,x,y2) private(j) for(i=0; i<m; i++) { y2[i] = 0.0; for(j=0; j<n; j++) y2[i] += A[i][j] * x[j]; } OMP_MatVec_for.c