
Decision-Procedure Based Theorem Provers Tactic-Based Theorem Proving Inferring Loop Invariants CS294-8 Lecture 12 Prof.Necula CS 294-8 Lecture 12 1
Prof. Necula CS 294-8 Lecture 12 1 Decision-Procedure Based Theorem Provers Tactic-Based Theorem Proving Inferring Loop Invariants CS 294-8 Lecture 12
Review Source language VCGen FOL Theories Goal-directed Sat.proc Sat.proc proving 1 n Prof.Necula CS 294-8 Lecture 12 2
Prof. Necula CS 294-8 Lecture 12 2 Review Source language VCGen FOL Theories Sat. proc 1 Sat. proc n Goal-directed proving … ?

Combining Satisfiability Procedures Consider a set of literals F Containing symbols from two theories Ti and Ta We split F into two sets of literals Fi containing only literals in theory Ti F2 containing only literals in theory T2 We name all subexpressions: pi(f2(E))is split into f2(E)=n^pi(n) We have:unsat (F1A F2)iff unsat(F) unsat(F)v unsat(F2)=unsat(F) But the converse is not true So we cannot compute unsat(F)with a trivial combination of the sat.procedures for Ti and Ta Prof.Necula CS 294-8 Lecture 12 3
Prof. Necula CS 294-8 Lecture 12 3 Combining Satisfiability Procedures • Consider a set of literals F – Containing symbols from two theories T1 and T2 • We split F into two sets of literals – F1 containing only literals in theory T1 – F2 containing only literals in theory T2 – We name all subexpressions: p1 (f2 (E)) is split into f2 (E) = n p1 (n) • We have: unsat (F1 F2 ) iff unsat(F) – unsat(F1 ) unsat(F2 ) unsat(F) – But the converse is not true • So we cannot compute unsat(F) with a trivial combination of the sat. procedures for T1 and T2

Combining Satisfiability Procedures.Example Consider equality and arithmetic ffx)-fy)≠fz) x≤y y+Z≤X 0≤Z y≤x X- f(x)=f(y) 0=Z fx)-fy)=z false← f(f(x)-f(y))=f(z) Prof.Necula CS 294-8 Lecture 12 4
Prof. Necula CS 294-8 Lecture 12 4 Combining Satisfiability Procedures. Example • Consider equality and arithmetic f(f(x) - f(y)) f(z) x y y + z x 0 z false f(x) = f(y) y x x = y 0 = z f(x) - f(y) = z f(f(x) - f(y)) = f(z)

Combining Satisfiability Procedures Combining satisfiability procedures is non trivial And that is to be expected: Equality was solved by Ackerman in 1924,arithmetic by Fourier even before,but E+A only in 1979 yet in any single verification problem we will have literals from several theories: Equality,arithmetic,lists,... When and how can we combine separate satisfiability procedures? Prof.Necula CS 294-8 Lecture 12 5
Prof. Necula CS 294-8 Lecture 12 5 Combining Satisfiability Procedures • Combining satisfiability procedures is non trivial • And that is to be expected: – Equality was solved by Ackerman in 1924, arithmetic by Fourier even before, but E + A only in 1979 ! • Yet in any single verification problem we will have literals from several theories: – Equality, arithmetic, lists, … • When and how can we combine separate satisfiability procedures?

Nelson-Oppen Method (1) 1. Represent all conjuncts in the same DAG f(f(x)-f(y)≠f(z)∧Y≥×∧×≥Y+z∧z≥0 X Z 0 Prof.Necula CS 294-8 Lecture 12 6
Prof. Necula CS 294-8 Lecture 12 6 Nelson-Oppen Method (1) 1. Represent all conjuncts in the same DAG f(f(x) - f(y)) f(z) y x x y + z z 0 f - f f y x z 0 + f

Nelson-Oppen Method (2) 2.Run each sat.procedure Require it to report all contradictions (as usual) Also require it to report all equalities between nodes f Z、 Prof.Necula CS 294-8 Lecture 12 7
Prof. Necula CS 294-8 Lecture 12 7 Nelson-Oppen Method (2) 2. Run each sat. procedure • Require it to report all contradictions (as usual) • Also require it to report all equalities between nodes f - f f y x z 0 + f
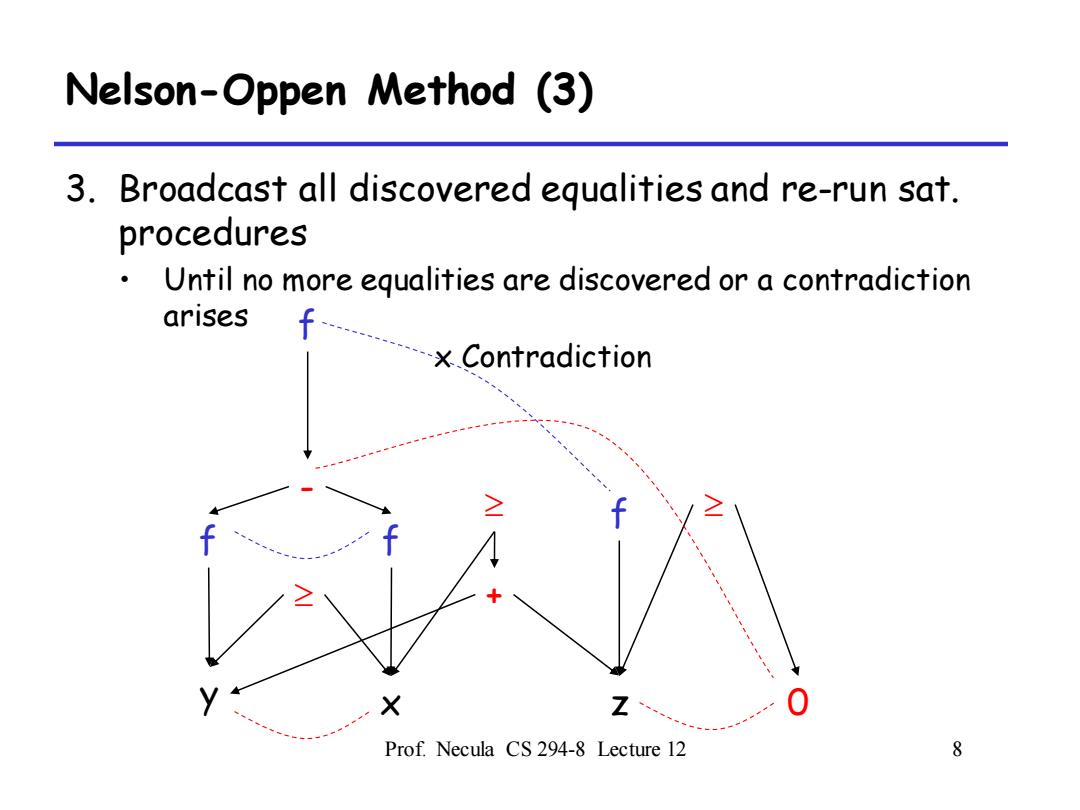
Nelson-Oppen Method (3) 3.Broadcast all discovered equalities and re-run sat. procedures Until no more equalities are discovered or a contradiction arises f x Contradiction Z、 Prof.Necula CS 294-8 Lecture 12 8
Prof. Necula CS 294-8 Lecture 12 8 Nelson-Oppen Method (3) 3. Broadcast all discovered equalities and re-run sat. procedures • Until no more equalities are discovered or a contradiction arises f - f f y x z 0 + f x Contradiction

What Theories Can be Combined? Only theories without common interpreted symbols But Ok if one theory takes the symbol uninterpreted Only certain theories can be combined Consider (Z,+,and Equality -Consider:1≤×≤2Λa=1Ab=2∧f(X)≠f(a)Af(X)≠f(b) No equalities and no contradictions are discovered yet,unsatisfiable A theory is non-convex when a set of literals entails a dis junction of equalities without entailing any single equality Prof.Necula CS 294-8 Lecture 12 9
Prof. Necula CS 294-8 Lecture 12 9 What Theories Can be Combined? • Only theories without common interpreted symbols – But Ok if one theory takes the symbol uninterpreted • Only certain theories can be combined – Consider (Z, +, ·) and Equality – Consider: 1 x 2 a = 1 b = 2 f(x) f(a) f(x) f(b) – No equalities and no contradictions are discovered – Yet, unsatisfiable • A theory is non-convex when a set of literals entails a disjunction of equalities without entailing any single equality

Handling Non-Convex Theories Many theories are non-convex Consider the theory of memory and pointers It is not-convex: trueA=A'v sel(upd(M,A,V),A')=sel(M,A) (neither of the dis juncts is entailed individually) For such theories it can be the case that No contradiction is discovered No single equality is discovered - But a disjunction of equalities is discovered We need to propagate disjunction of equalities.. Prof.Necula CS 294-8 Lecture 12 10
Prof. Necula CS 294-8 Lecture 12 10 Handling Non-Convex Theories • Many theories are non-convex • Consider the theory of memory and pointers – It is not-convex: true A = A’ sel(upd(M, A, V), A’) = sel(M, A’) (neither of the disjuncts is entailed individually) • For such theories it can be the case that – No contradiction is discovered – No single equality is discovered – But a disjunction of equalities is discovered • We need to propagate disjunction of equalities …