
第一节定积分的概念与性质 一、定积分问题举例 二、定积分定义 三、定积分的近似计算 四、定积分的性质 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 定积分的概念与性质 一、定积分问题举例 二、定积分定义 三、定积分的近似计算 四、定积分的性质
第一节定积分的概念与性质 一、定积分问题举例 1.曲边梯形的面积 我们已经会求规则平面图形的面积,如 矩形 平行四边形 三角形 梯形 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 定积分的概念与性质 一、定积分问题举例 1. 曲边梯形的面积 我们已经会求规则平面图形的面积,如 矩形 平行四边形 三角形 梯形

第一节定积分的概念与性质 那么如何求不规则平面图形的面积呢?如 y =1.5xsin x -2L 2 X 下面来研究这个问题. 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 定积分的概念与性质 那么如何求不规则平面图形的面积呢?如 下面来研究这个问题. x y y =1.5xsin x -2 2 O
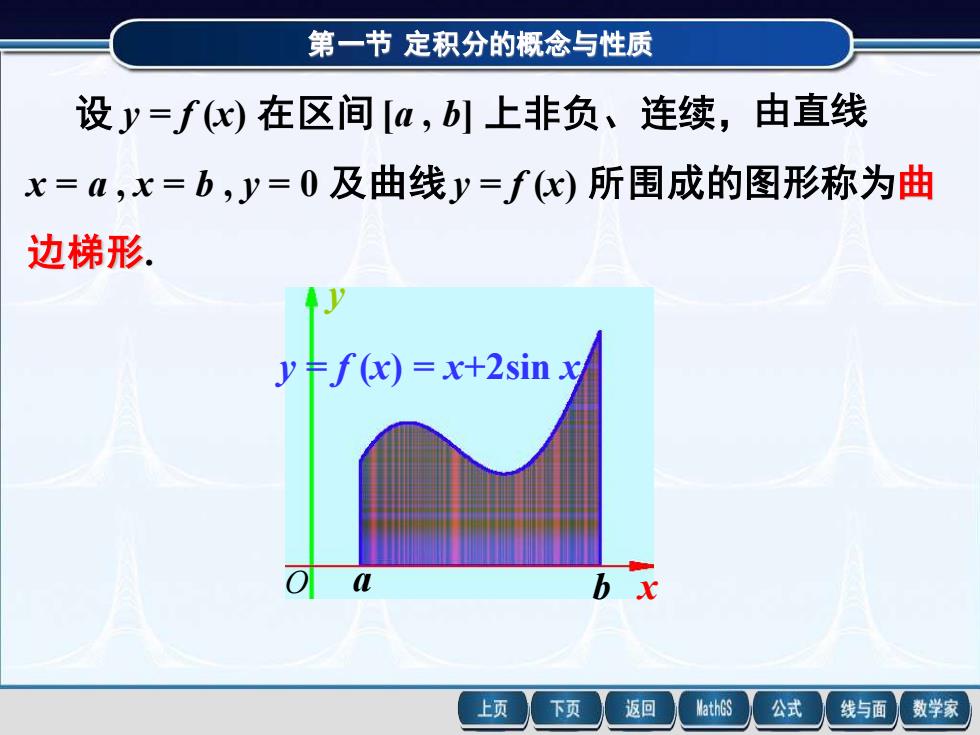
第一节定积分的概念与性质 设y=f心)在区间[a,b1上非负、连续,由直线 x=,x=b,y=0及曲线y=f(x)所围成的图形称为曲 边梯形 y卡f(x)=x+2sinx 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 定积分的概念与性质 设 y = f (x) 在区间 [a , b] 上非负、连续,由直线 x = a , x = b , y = 0 及曲线 y = f (x) 所围成的图形称为曲 边梯形. x y a b y = f (x) = x+2sin x O
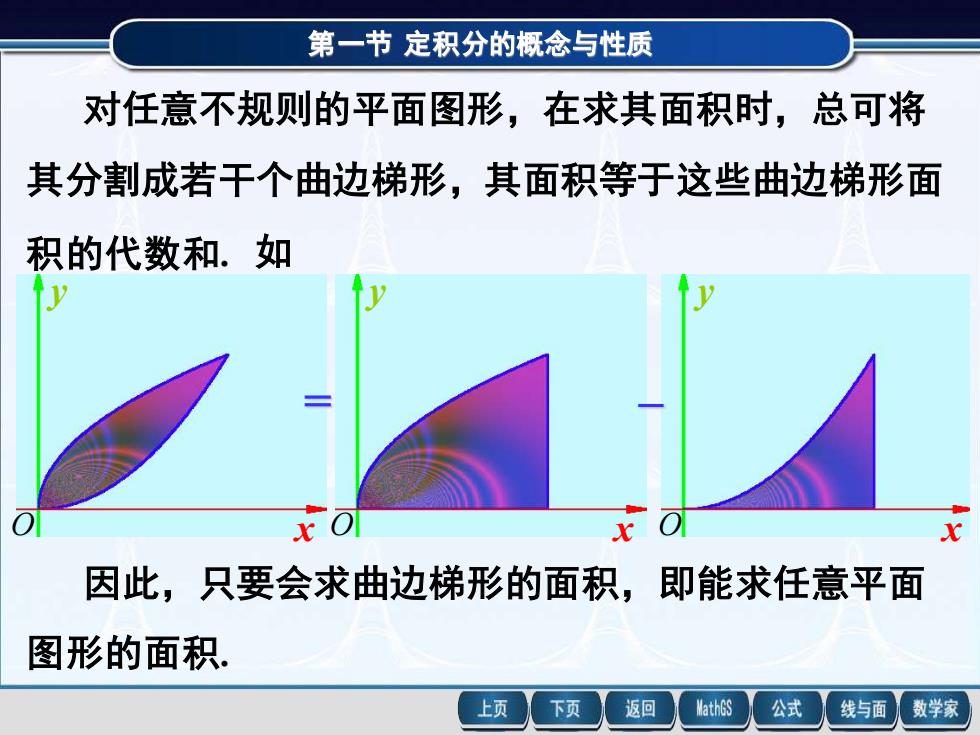
第一节定积分的概念与性质 对任意不规则的平面图形,在求其面积时,总可将 其分割成若干个曲边梯形,其面积等于这些曲边梯形面 积的代数和.如 1 因此,只要会求曲边梯形的面积,即能求任意平面 图形的面积. 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 定积分的概念与性质 O x y O x y O x y 对任意不规则的平面图形,在求其面积时,总可将 其分割成若干个曲边梯形,其面积等于这些曲边梯形面 积的代数和. 如 = – 因此,只要会求曲边梯形的面积,即能求任意平面 图形的面积
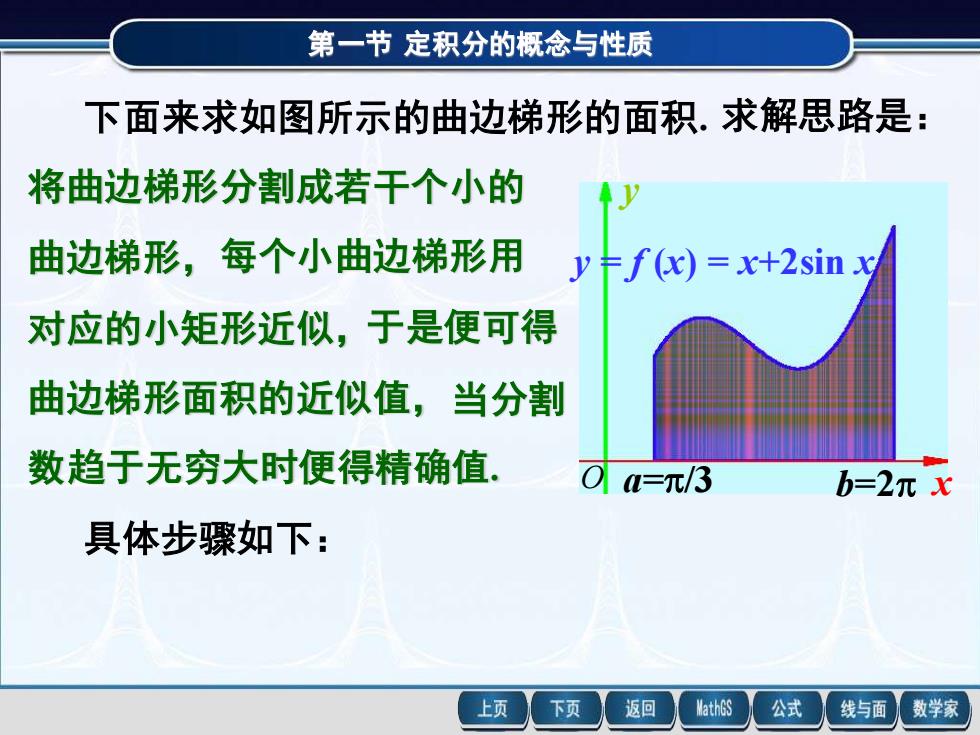
第一节定积分的概念与性质 下面来求如图所示的曲边梯形的面积.求解思路是: 将曲边梯形分割成若干个小的 曲边梯形,每个小曲边梯形用 y=f(x)=x+2sinx 对应的小矩形近似,于是便可得 曲边梯形面积的近似值,当分割 数趋于无穷大时便得精确值. M=元/3 b=2元x 具体步骤如下: 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 定积分的概念与性质 下面来求如图所示的曲边梯形的面积. 求解思路是: 将曲边梯形分割成若干个小的 曲边梯形,每个小曲边梯形用 对应的小矩形近似,于是便可得 曲边梯形面积的近似值,当分割 数趋于无穷大时便得精确值. 具体步骤如下: a=/3 b=2 x y y = f (x) = x+2sin x O
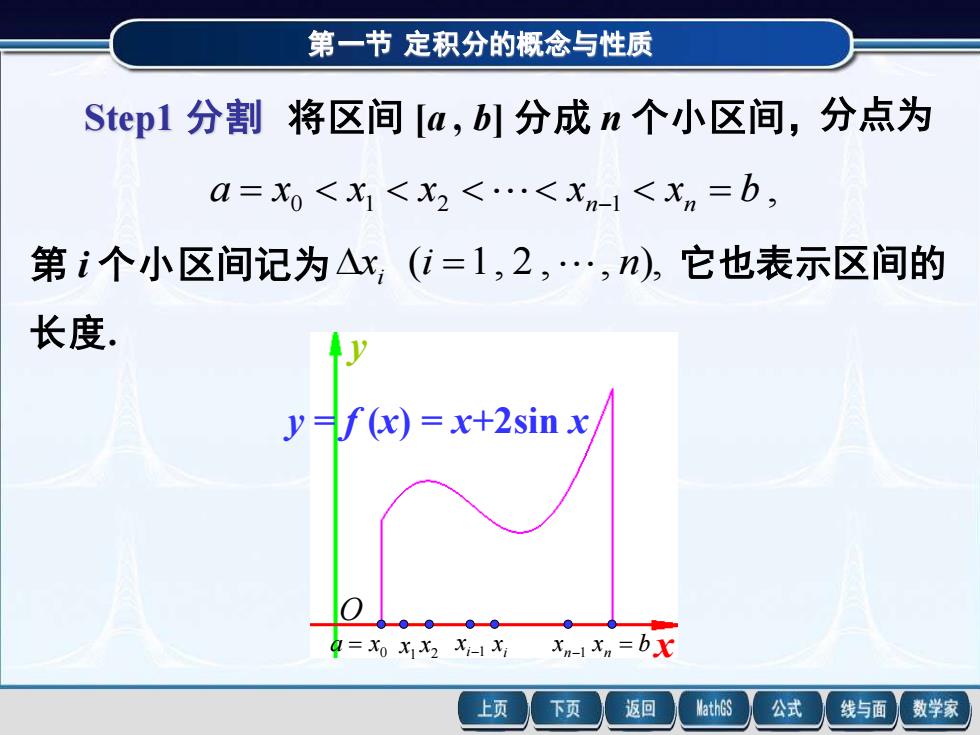
第一节定积分的概念与性质 Step1分割将区间[a,b]分成n个小区间,分点为 a=x0<x<X2<.<X-<X=b, 第i个小区间记为△x(i=1,2,.,n),它也表示区间的 长度, y=f(x)=x+2sin x a=X0 XX2 Xi-X Xn-1X=bx 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 定积分的概念与性质 Step1 分割 将区间 [a , b] 分成 n 个小区间,分点为 , a = x0 x1 x2 xn−1 xn = b 第 i 个小区间记为 x (i 1, 2 , , n), i = 它也表示区间的 长度. x y y = f (x) = x+2sin x 0 a = x 1 x 2 x i−1 x i x n−1 x x b n = O

第一节定积分的概念与性质 Step2近似以每个小区间为底,以f(5)(5,∈△x) 为高作矩形,并以矩形来近似相应的小曲边梯形 y=f(x)=x+2sin x y=f(x)=x+2sin x Q=xx为2xx,xm-1xn=bX 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 定积分的概念与性质 Step2 近似 以每个小区间为底,以 ( ) ( ) i i i f x 为高作矩形,并以矩形来近似相应的小曲边梯形. x y y = f (x) = x+2sin x 0 a = x 1 x 2 x i−1 x i x n−1 x x b n = O x y y = f (x) = x+2sin x O
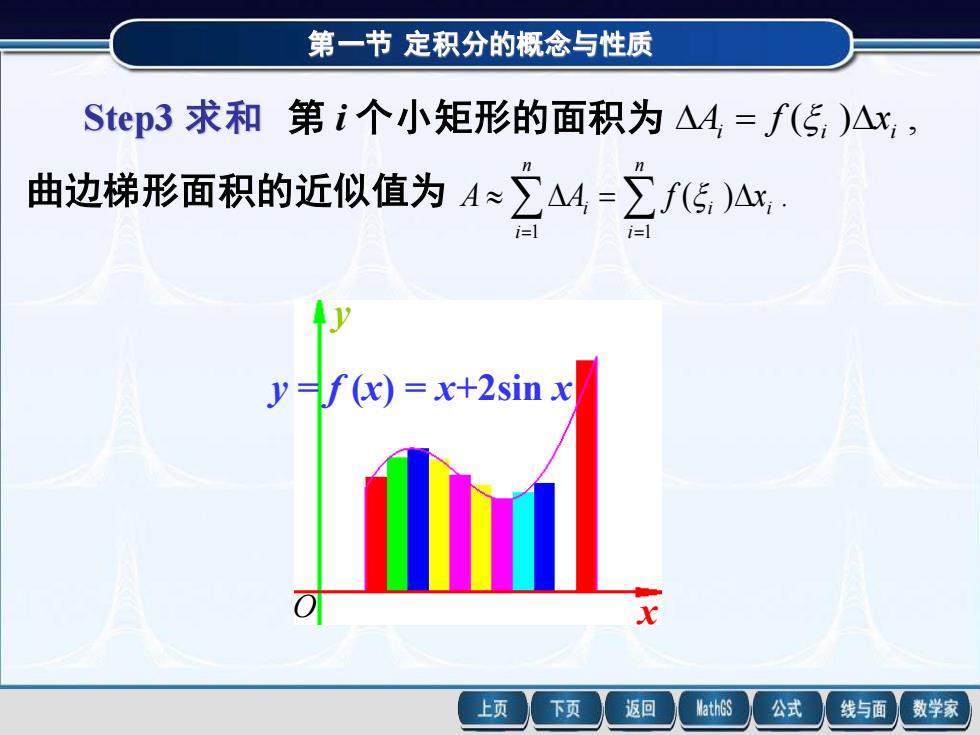
第一节定积分的概念与性质 Step3求和第i个小矩形的面积为△A=f(5,)△x, 曲边梯形面积的近似值为A≈∑AA=∑f(传,)Ax y=f(x)=x+2sin x 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 定积分的概念与性质 Step3 求和 第 i 个小矩形的面积为 ( ) , i i i A = f x 曲边梯形面积的近似值为 ( ) . 1 1 = = = n i i i n i i A A f x x y y = f (x) = x+2sin x O

第一节定积分的概念与性质 Step4取极限 A=lim2A4=lim2f传)ax, 10 0 i=l 其中2为n个小区间长度中的最大值. y=f(x)=x+2sin x yf(x)=x+2sin x 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 定积分的概念与性质 Step4 取极限 其中 为 n 个小区间长度中的最大值. ( ) , 0 1 0 1 lim lim → = → = = = n i i i n i i A A f x x y y = f (x) = x+2sin x O x y y = f (x) = x+2sin x O