
第6章 LR分析程序及其自动构造 6.1 自下而上分析及其LR分析概述 6.2 LR (O) 分析 6.3 SLR(1) 分析 6.4 LR(1)分析 6.5 LALR分析 6.6 使用二义文法
第6章 LR分析程序及其自动构造 6.1 自下而上分析及其LR分析概述 6.2 LR (0) 分析 6.3 SLR(1) 分析 6.4 LR(1)分析 6.5 LALR分析 6.6 使用二义文法
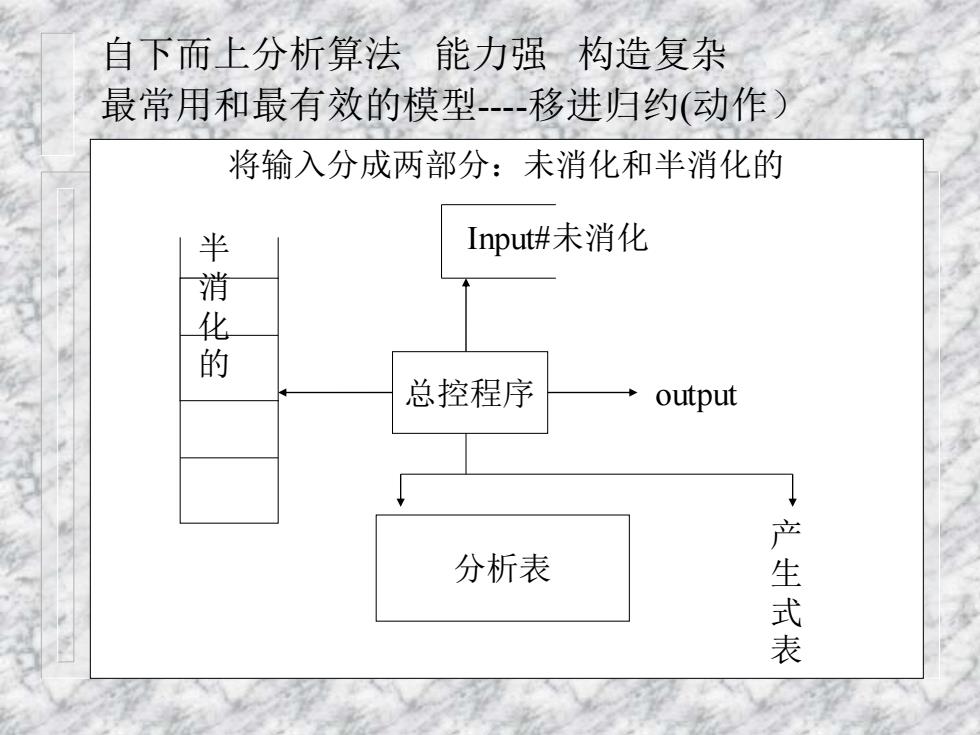
自下而上分析算法能力强构造复杂 最常用和最有效的模型-移进归约(动作) 将输入分成两部分:未消化和半消化的 半 Input#未消化 化 总控程序 output 分析表 产生式表
自下而上分析算法 能力强 构造复杂 最常用和最有效的模型----移进归约(动作) 总控程序 output Input# … 栈 状态 文法符号 分析表 产 生 式 表 将输入分成两部分:未消化和半消化的 总控程序 output 半 Input#未消化 消 化 的 分析表 产 生 式 表

S->E E->TE+T T->int|(E) Reduce:如能找到一产生式A->w且栈中的内容是qw (q可能为空),则可以将其归约为qA即过来用这个 产生式 如上例,若栈中内容是(int,我们使用产生式T->int 柄把栈中内容归约为(T Sh:如不能执行一个归约且在未消化的输入中还有 token,就把它从输入移到栈中 如上例,假定栈中内容是(,输入中还有int+int)#.不能 对(执行一个归约,因为它不和任何产生式的右端匹 配所以把输入的第一个符号移到栈中,于是栈中内容 是(int,而余留的输入是+int)#
S –> E E –> T | E + T T –> int | (E) Reduce: 如能找到一产生式 A –> w 且栈中的内容是 qw (q 可能为空), 则可以将其归约为 qA.即倒过来用这个 产生式. 如上例, 若栈中内容是 (int ,我们使用产生式 T–> int 柄把栈中内容归约为(T Shift: 如不能执行一个归约且在未消化的输入中还有 token ,就把它从输入移到栈中. 如上例,假定栈中内容是 ( ,输入中还有 int+int)#.不能 对( 执行一个归约,因为它不和任何产生式的右端匹 配.所以把输入的第一个符号移到栈中,于是栈中内容 是 (int ,而余留的输入是 +int)#

Reducel的一个特殊情况:栈中的全部内容 w归约为开始符号S(即施用S->w) 且没有余留输入了,意味着已成功分析 了整个输入串 移进归分析中还会出现一种情况,就是 出错,比如当前的token不能构成一个合 法句子的一部分,例如上面的文法,试 分析int+)时就会发生错误
Reduce的一个特殊情况:栈中的全部内容 w归约为开始符号S (即施用 S –> w) , 且没有余留输入了,意味着已成功分析 了整个输入串. 移进归约分析中还会出现一种情况,就是 出错,比如当前的token不能构成一个合 法句子的一部分,例如上面的文法,试 分析 int+)时就会发生错误

STACK REMAINING INPUT PARSER ACTION 1 (int int)# Shift 2 int int)# Shift (int int)# Reduce:T->int 456789 int)# Reduce:E->T ( int)# Shift (E+ int)# Shift Reduce:T->int # Reduce:E->E+T (E )# Shift 10(E) # Reduce:T->(E) T Reduce:E-> T 12E Reduce:S->E 13S 井井#
STACK REMAINING INPUT PARSER ACTION 1 (int + int)# Shift 2 ( int + int)# Shift 3 (int + int)# Reduce: T –> int 4 (T + int)# Reduce: E –> T 5 (E + int)# Shift 6 (E + int)# Shift 7 (E + int )# Reduce: T –> int 8 (E + T )# Reduce: E –> E + T 9 (E )# Shift 10 (E) # Reduce: T –> (E) 11 T # Reduce: E –> T 12 E # Reduce: S –> E 13 S #

8 (E+T )# Reduce:E->E+T 9 why?不用E->T 9 (E )# 若使用了E->T,在栈中形成的(E+E不是规范句 型的活前缀(viable prefixes) (E+E不能和任何产生式的右端匹配(E+E)不是 规范句型 活前缀是规范句型(右句型)的前缀,但不超过 句柄 移进归约分析的栈中出现的内容加上余留输入 构成规范句型
8 (E + T )# Reduce:E –> E + T 9 why?不用 E –> T 9 (E ) # 若使用了E –> T,在栈中形成的(E+E不是规范句 型的活前缀(viable prefixes) (E+E不能和任何产生式的右端匹配 (E+E)不是 规范句型 活前缀 是规范句型(右句型)的前缀,但不超过 句柄 ❖ 移进归约分析的栈中出现的内容加上余留输入 构成规范句型

规范推导规范句型规范归约 最右推导:在推导的任何一步a→B,其中a、B是句型,都是对α中 的最右非终结符进行替换 最右推导被称为规范推导。 由规范推导所得的句型称为规范句型 GS:S→EE→E+rlTT→(E)|int S→E→T→(E)→(E+T)→(E+int) →(T+int)→(int+int) 规范归约 假定a是G的一个句子,称序列an,an1,a是a的一个规范归约 如果该序列满足: (1)an= a (2)a。为文法的开始符号 (3)对任何j,0心j=n,aj-1是从a经把句柄替换为相应产生式的左部 而得到的
规范推导 规范句型 规范归约 最右推导:在推导的任何一步αβ,其中α、β是句型,都是对α中 的最右非终结符进行替换 最右推导被称为规范推导。 由规范推导所得的句型称为规范句型 G[S]: S→E E→E+T|T T→(E)|int SE T (E) (E+T) (E+int) (T+int) (int+int) 规范归约 假定α是G的一个句子,称序列αn ,αn-1 …,α0是 α的一个规范归约 如果该序列满足: (1) αn = α (2) α0为文法的开始符号 (3)对任何j,0<j<=n, αj-1是从αj经把句柄替换为相应产生式的左部 而得到的

文法要求 shift-reduce or reduce-reduce (conflicts) 分析程序不能决定是shift还是reduce 或者分析程序归约时有多个产生式可选 例子(dangling else): S->if E then S if E then S else S 如输入if E then if E then S else S 分析某一时刻,栈的内容:if E then if E then S 而else是下一token归约还是移进?
文法要求 shift-reduce or reduce-reduce 冲突(conflicts) 分析程序不能决定是shift 还是 reduce 或者分析程序归约时有多个产生式可选 例子 ( dangling else) : S –> if E then S | if E then S else S 如输入if E then if E then S else S 分析某一时刻,栈的内容:if E then if E then S 而 else 是下一 token 归约还是移进?

特定的一种shif-reduce实现技术 LR分析 L R最右推导 分析器模型和分析算法 工R分析特征讨论
特定的一种shift-reduce实现技术 LR分析 L R 最右推导 分析器模型和分析算法 LR 分析特征讨论
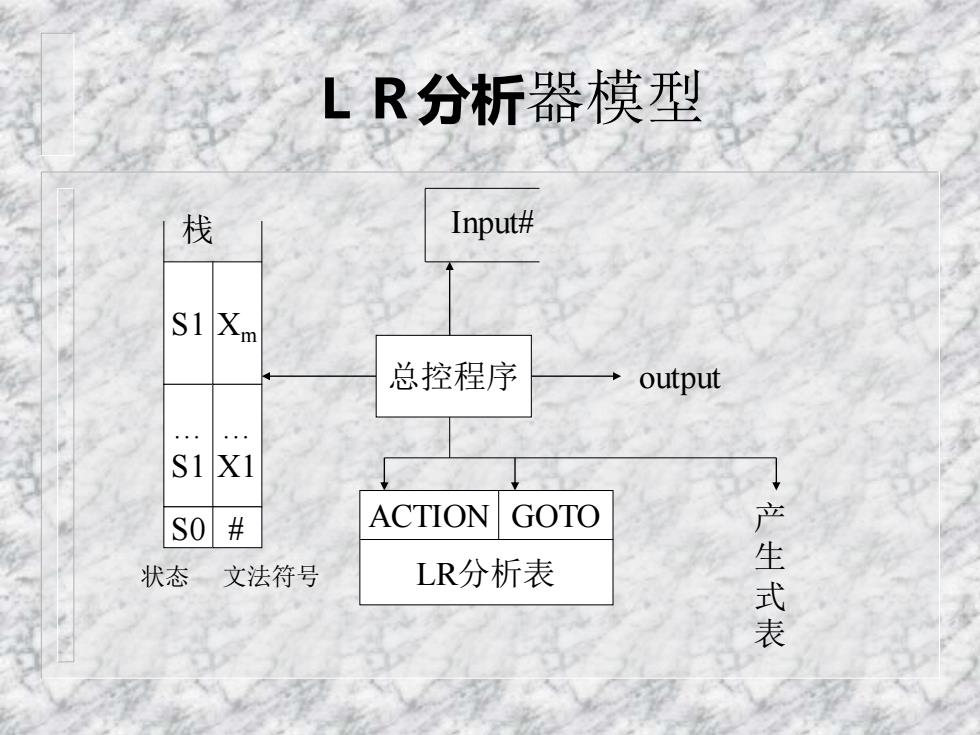
LR分析器模型 栈 Input# S1Xm 总控程序 output S1X1 S0# ACTION GOTO 状态文法符号 LR分析表 产生式表
LR分析器模型 总控程序 output Input# S1 Xm … S1 … X1 S0 # 栈 状态 文法符号 ACTION GOTO LR分析表 产 生 式 表