
2.3句型的分析 句型的分析:构造一算法,用以判断所给 的符号串是否为某文法的句型(句子) 常见分析方法有自顶向下分析和自底向上 分析两类; 自顶向下从开始符出发试图推导出给定的 符号串; 自底向上推导的逆过程(称归约):从已 给的符号串出发,试图将其归约为开始符
2.3 句型的分析 • 句型的分析:构造一算法,用以判断所给 的符号串是否为某文法的句型(句子) • 常见分析方法有自顶向下分析和自底向上 分析两类; • 自顶向下 从开始符出发试图推导出给定的 符号串; • 自底向上 推导的逆过程(称归约):从已 给的符号串出发,试图将其归约为开始符

2.3.1规范推导和规范归约 ·对于一文法而言,从开始符到某句型的推导过程可能不唯 一。例如,文法G[E]中从E到+*的推导有: (1)E→E+T台E+T*F→T+T*F→T+T*i三→F+T*i→→i+T*i三 i+F*i→i+i*i (2)E→E+T→T+T→F+T→i+T台i+T*F→i+F*F→→i+i*F →i+i*F→i+i*i (3)E→E+T→E+T*℉→E+T*i→E+E*i→E+i*i→→I+i*i→ F+i*i→i+i*i (4)..… 心
2.3.1 规范推导和规范归约 • 对于一文法而言,从开始符到某句型的推导过程可能不唯 一。例如,文法G[E]中从 E 到 i+i*i 的推导有: (1)E E+T E+T*F T+T*F T+T*i F+T*i i+T*i i+F*ii+i*i (2)E E+T T+T F+T i+T i+T*F i+F*F i+i*F i+i*F i+i*i (3)E E+T E+T*F E+T*i E+F*i E+i*i T+i*i F+i*i i+i*i (4) … …

规范推导 ·为了让计算机自动地进行推导,通常我们只考虑最左或最 右推导。 ·最左(右)推导:在推导序列的每一步直接推导中,被替 换的总是当前句型中最左(右)的非终结符。 ·例如,上页中的(2)、(3)分别是最左、最右推导。 形式上,从符号串o到符号串β的推导序列 a→*xUy→xuy→*B总有x∈V,*(y∈V) 时,称为最左(右)推导 定义:最左(右)推导所得句型称为左(右)句型;最右 推导称为规范推导;右句型称为规范句型
规范推导 • 为了让计算机自动地进行推导,通常我们只考虑最左或最 右推导。 • 最左(右)推导:在推导序列的每一步直接推导中,被替 换的总是当前句型中最左(右)的非终结符。 • 例如,上页中的(2)、(3)分别是最左、最右推导。 • 形式上,从符号串到符号串的推导序列 * xUy xuy * 总有 xVT * (yVT *) 时,称为最左(右)推导 • 定义:最左(右)推导所得句型称为左(右)句型;最右 推导称为规范推导;右句型称为规范句型

句子、句型的推导方法 每个句子都有相应的最左和最右推导,因此,句子即是左句型 也是右句型(规范句型) ·并不是每个句型都有最左和最右推导 ·例如,E→+E+i*T即不是左句型,也不是右句型 ·对于给定的符号串w,采用自顶向下的分析来判断w是否为 L(G[S)的句子的常见方法是:试图建立从开始符S到w最左推 导:S→w ·显然,每步推导时,对应于最左非终结符相应的产生式可能会 有多个,若无特殊的办法,只能一个一个地试探。因此,推导 过程可能是带回湖的。 ·为提高效率,就应尽量避免回溯
句子、句型的推导方法 • 每个句子都有相应的最左和最右推导,因此,句子即是左句型 也是右句型(规范句型) • 并不是每个句型都有最左和最右推导 • 例如,E + E+i*T即不是左句型,也不是右句型 • 对于给定的符号串w,采用自顶向下的分析来判断w是否为 L(G[S])的句子的常见方法是:试图建立从开始符 S到w最左推 导: S * w • 显然,每步推导时,对应于最左非终结符相应的产生式可能会 有多个,若无特殊的办法,只能一个一个地试探。因此,推导 过程可能是带回溯的。 • 为提高效率,就应尽量避免回溯

自底向上的语法分析 ~就是从已给的符号串w出发,试图以相反的方向为W建立一个规 范推导,最终得到文法的开始符。 推导的逆过程称作归约,它是把当前的符号串Baδ冲的构成文法 某个产生式A→a右部的子串a替换成产生式的左部符号A,得到 一个新的符号串A6。这样的一步动作,称为进行了一步归约。 · 例如,符号串F+*中的F可按产生式T→F归约为T,从而得到新 的符号串T+*i。 若从给定的符号串出发,一步步地将其归约,最终得到文法的 开始符号,则说明是该文法定义的一个句子。归约成功,否则, 归约失败。 若归约的每一步都归约的是当前符号串中最左边的某产生式的右 部,则称该归约是规范归约(即最左归约)。 规范归约是规范推导的逆过程。 关于最左(右)归约、直接归约、归约等的形式定义不再赘述
自底向上的语法分析 • ~就是从已给的符号串w出发,试图以相反的方向为w建立一个规 范推导,最终得到文法的开始符。 • 推导的逆过程称作归约,它是把当前的符号串中的构成文法 某个产生式A→右部的子串替换成产生式的左部符号A,得到 一个新的符号串A 。这样的一步动作,称为进行了一步归约。 • 例如,符号串F+i*i中的F可按产生式T→F归约为T,从而得到新 的符号串T+i*i。 • 若从给定的符号串w出发,一步步地将其归约,最终得到文法的 开始符号,则说明w是该文法定义的一个句子。归约成功,否则, 归约失败。 • 若归约的每一步都归约的是当前符号串中最左边的某产生式的右 部,则称该归约是规范归约(即最左归约)。 • 规范归约是规范推导的逆过程。 • 关于最左(右)归约、直接归约、归约等的形式定义不再赘述
将号串i+i*i的▣约过程 步序 当前符号串W 所用的产生式 归约后的符号 iti*i F→i F+i*i 1 F+i*i T→F T+i*i T+i*i E→T E+i*i 3 E+i*i F→i E+F*i E+F*i T→F E+T*i E+T*i F-i E+T*F 6 E+T*F T→T*F E+T 7 E+T E→E+T E 由上表可以看出, 归约过程是最左归约,它恰好是规 范推导的逆过程。这正是把最左归约定义为规范归约 的原因
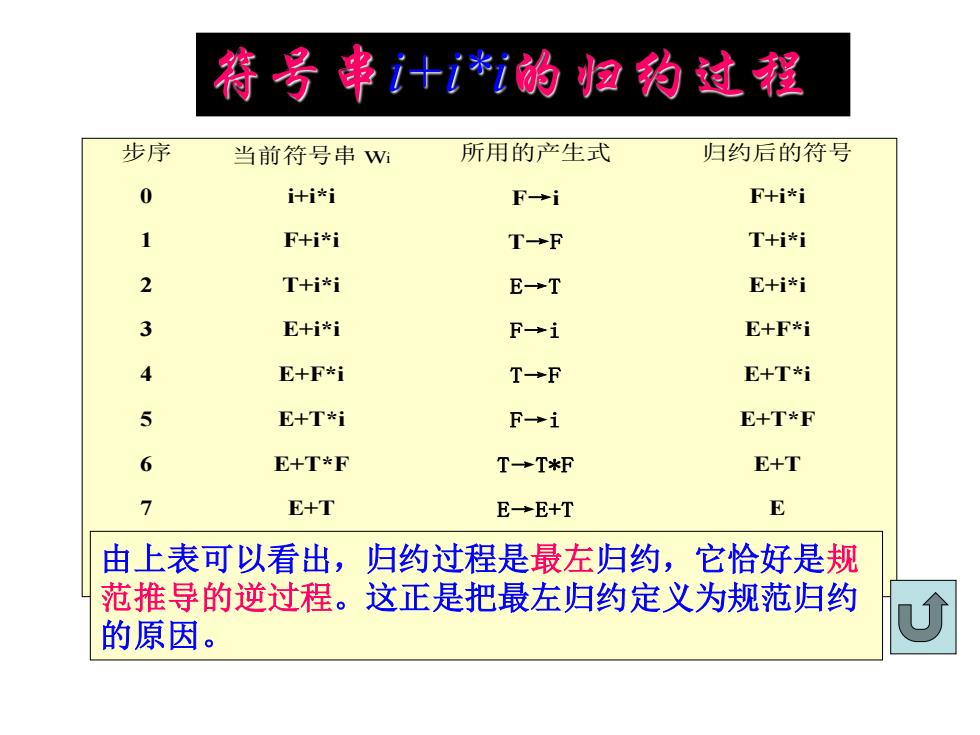
符号串i+i*i的归约过程 步序 当前符号串 wi 所用的产生式 归约后的符号 0 i+i*i F→i F+i*i 1 F+i*i T→F T+i*i 2 T+i*i E→T E+i*i 3 E+i*i F→i E+F*i 4 E+F*i T→F E+T*i 5 E+T*i F→i E+T*F 6 E+T*F T→T*F E+T 7 E+T E→E+T E 由上表可以看出,归约过程是最左归约,它恰好是规 范推导的逆过程。这正是把最左归约定义为规范归约 的原因

关于归约的一点说明 ·注意,前面例子中归约的第五步中,当前的符号串为 E+*i,除了可将归约成F外,还可将E+T或T归约成E, 分别得到符号串E*和E+E*i。但是,若真按这两个方案 进行归约,则当我们把其归约成E*E或E+E*E时,就再 也归约不下去了。这就告诉我们在第五步时,唯一正确 的归约是将归约为F,也就是说,是唯一可被归约的最 左子串。 那么,对于规范归约的每一步,如何确定符号串中的当 前应被归约的最左子串呢? ·这里暂且按下不提,且听2.3.3小节分解
关于归约的一点说明 • 注意,前面例子中归约的第五步中,当前的符号串为 E+T*i,除了可将i归约成F外,还可将E+T或T归约成E, 分别得到符号串E*i和E+E*i。但是,若真按这两个方案 进行归约,则当我们把其归约成E*E或E+E*E时,就再 也归约不下去了。这就告诉我们在第五步时,唯一正确 的归约是将i归约为F,也就是说,i是唯一可被归约的最 左子串。 • 那么,对于规范归约的每一步,如何确定符号串中的当 前应被归约的最左子串呢? • 这里暂且按下不提,且听2.3.3小节分解

2.32语法对和号义性 ·语法树用于直接地描述一个句型右句子的语法结构 语法树是一有向树(连通的) 1)有且仅有一个无任何前驱的结点,称为根(S); 2)除根外,每个结点恰有一个直接前驱; 3)对于任一结点m,从根m可达, 4)每个结点的后继是有序的(从左到右) 。 设G=,V,PS)是一文法,则满足下述条件的树称为语法树: 1)每个结点有一标记X,XeV; 2)根的标记为S(开始符); 3)若结点X有后继,则XEVw; 4)A有k个后继,自左至右为X,X,X,则A→XX.X∈P
2.3.2 语法树和二义性 • 语法树用于直接地描述一个句型右句子的语法结构 • 语法树是一有向树(连通的) 1)有且仅有一个无任何前驱的结点,称为根 (S); 2)除根外,每个结点恰有一个直接前驱; 3)对于任一结点m,从根到m可达; 4) 每个结点的后继是有序的(从左到右) • 设G=(VN,VT,P,S)是一文法,则满足下述条件的树称为语法树: 1)每个结点有一标记X,XV; 2)根的标记为S(开始符); 3)若结点X有后继,则XVN; 4)A有k个后继,自左至右为X1, X2, …, Xk,则A→ X1X2…Xk P
语法树的性质及实例 。 语法树的所有叶结点自 E 左至右排列构成了文法G 的一个句型 ·对一语法树而言,其构造 过程不同对应了不同的推 导(归约)过程 例如,文法GE的句型 +*相应的语法树见右图。 i
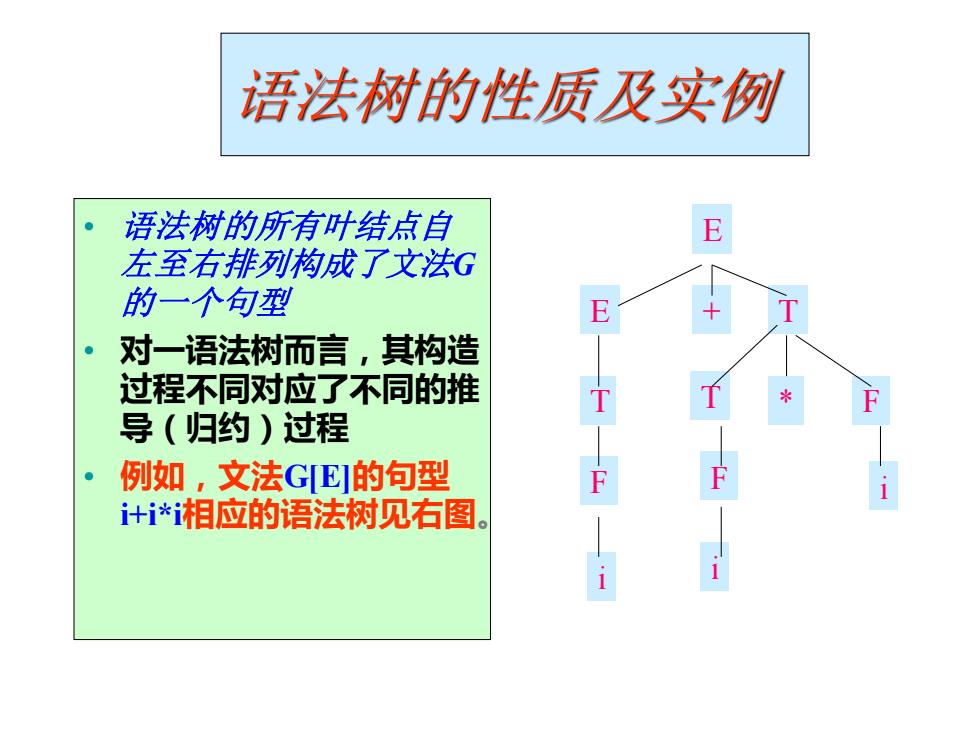
语法树的性质及实例 • 语法树的所有叶结点自 左至右排列构成了文法G 的一个句型 • 对一语法树而言,其构造 过程不同对应了不同的推 导(归约)过程 • 例如,文法G[E]的句型 i+i*i相应的语法树见右图。 E E + T T F i T * F F i i

文法的二义性 存在这样的文法G,其某个句子wL(G),可对应结构不 同的语法树,即W对应了多个不同的最左 (右)推导, 这类文法称为二义性文法。 例如,G3E]:E→E+EE*E(E)的句型+及文法 。 c->ifB then Clif B then C else C C→S 的句型:fB1 then if B2 then S1 else S2 上面两个句型均有两个不同的语法推导树(见下页), 所以,它们是二义性文法
文法的二义性 • 存在这样的文法G,其某个句子wL(G),可对应结构不 同的语法树,即w对应了多个不同的最左(右)推导, 这类文法称为二义性文法。 • 例如,G3[E]:E→E+E|E*E|(E)|i 的句型i+i*i及文法 • C→if B then C|if B then C else C C →S 的句型:if B1 then if B2 then S1 else S2 • 上面两个句型均有两个不同的语法推导树(见下页), 所以,它们是二义性文法