
5.3常见中向语言简个 ·在着手讨论各种语法结构的语法制导翻译 之前,我们首先应介绍一下目前经常使用 的几种中间语言的形式。这是因为,语义 子程序的设计,不仅依赖于相应语法结构 中各个量的语义,而且还取决于要产生什 么形式的中间代码
5.3 常见中间语言简介 • 在着手讨论各种语法结构的语法制导翻译 之前,我们首先应介绍一下目前经常使用 的几种中间语言的形式。这是因为,语义 子程序的设计,不仅依赖于相应语法结构 中各个量的语义,而且还取决于要产生什 么形式的中间代码

5.3.1逆波兰表示 ·波兰逻辑学家].Lukasiewicz于1929年提出了另一种 表示表达式的方法。按此方法,每一运算符都置于其 运算对象之后,故称为后缀表示。 ·特点:表达式中各个运算是按运算符出现的顺序进行的, 故无须使用括号来指示运算顺序,因而又称为无括号 式。下面我们对照地给出一些表达式的两种表示: 中缀表示 后缀表示 A+B AB+ A+B*C ABC*+ (A+B)*(C+D) AB+CD+* x/y^z-d*e xyz^/de*- (a=Onb>3)v(enx<>y)a0=b3>nexy<>Av
5.3.1 逆波兰表示 • 波兰逻辑学家J.Lukasiewicz于1929年提出了另一种 表示表达式的方法。按此方法,每一运算符都置于其 运算对象之后,故称为后缀表示。 • 特点:表达式中各个运算是按运算符出现的顺序进行的, 故无须使用括号来指示运算顺序,因而又称为无括号 式。下面我们对照地给出一些表达式的两种表示: 中缀表示 后缀表示 A+B AB+ A+B*C ABC*+ (A+B)*(C+D) AB+CD+* x/y^z-d*e xyz^/de*- (a=0b>3)(ex<>y) a0=b3>exy<>

逆波玄式的特点 ①在两种表示中,运算对象出现的顺序相同; ②在后缀表示中,运算符按实际计算顺序从左到右排列, 且每一运算符总是跟在其运算对象之后。 由于后缀表示中的各个运算是按顺序执行的,因此, 它的计值需从左到右依次扫视表达式中的各个符号, ·每遇一运算对象,就把它压入栈顶暂存起来; ·每遇一个二元(或一元)运算符时,就取出栈顶的两 个(或一个)运算对象进行相应的运算,并用运算结 果去替换栈顶的这两(或一)个运算对象; 。1 继续扫视余留的符号,直到扫视完整个表达式为止。 ·当上述过程结束时,整个表达式的值将留于栈顶
逆波兰式的特点 ①在两种表示中,运算对象出现的顺序相同; ②在后缀表示中,运算符按实际计算顺序从左到右排列, 且每一运算符总是跟在其运算对象之后。 • 由于后缀表示中的各个运算是按顺序执行的,因此, 它的计值需从左到右依次扫视表达式中的各个符号, • 每遇一运算对象,就把它压入栈顶暂存起来; • 每遇一个二元(或一元)运算符时,就取出栈顶的两 个(或一个)运算对象进行相应的运算,并用运算结 果去替换栈顶的这两(或一)个运算对象; • 继续扫视余留的符号,直到扫视完整个表达式为止。 • 当上述过程结束时,整个表达式的值将留于栈顶

逆波兰表示的扩充 。逆波兰表示还可用于表示其它的语法结构。此时,运算符不再限于 算术、关系和逻辑运算符,每个运算符的操作对象也可以不止两 个。例如,赋值语句x:=a+b*c可按后缀式写为xabc*+:=。 ·为了用后缀式表示一些控制语句,我们假定将后缀式的各符号存 放在一个一维数组POST[]中.还需引入一些转移操作符: ·pBR一无条件转至POST[p](从POST[p]继续执行); ·e'pBZ一e'是e的后缀表示,当e'之值为零时,转向POST[p]; ● e1'e2'pBL-e1'和e2'分别是e1和e2的后缀表示,当e1'<e2 时,转向POST[p]: ● 类似地,我们还可以定义BN(非零转)、BP(正号转)、BM(负号 转)等等。于是,条件语句IF e THEN S1 ELSE S2可写成 e'p BZ S'p2 BR S2 其中,p表示S2在数组POST中的起始位置;P2表示位于S2之 后那个符号的位置
逆波兰表示的扩充 • 逆波兰表示还可用于表示其它的语法结构。此时,运算符不再限于 算术、关系和逻辑运算符,每个运算符的操作对象也可以不止两 个。例如,赋值语句x:=a+b*c可按后缀式写为x abc*+:=。 • 为了用后缀式表示一些控制语句,我们假定将后缀式的各符号存 放在一个一维数组POST[n]中.还需引入一些转移操作符: • p BR—无条件转至POST[p](从POST[p] 继续执行); • e’ p BZ—e’是e的后缀表示,当e’之值为零时,转向POST[p]; • e1’ e2’ p BL—e1’和e2’分别是e1和e2的后缀表示,当 e1’<e2’ 时,转向POST[p]; • 类似地,我们还可以定义BN(非零转)、BP(正号转)、BM(负号 转)等等。于是,条件语句IF e THEN S1 ELSE S2 可写成 e’ p1 BZ S1 ’ p2 BR S2 ‘ 其中, p1表示S2 ‘在数组POST中的起始位置; p2表示位于S2 ‘之 后那个符号的位置

例:翻译表达式的S-属性文法 我们以第3式为例介绍其原理。 l.Expr→ Expr,‘+'Term 首先,产生式左部Term的首地址显 {$$=$1;POST[p]=+'; 然应与右部第一符号对应的首地 p++} 址相同($$=$1;)。 2.|Term{$$=$l;} 其次,按第3式归约时,或者说, 3.Term→Term,'* Factor 翻译文法执行该语义动作时,右 {$$=$1;POST[p] =‘*} 部符号Term和Factor对应的输出 p++} (即各自所代表的代码段)已经 4.|Factor{.$$=$1;} 建立,并已存储在P0ST中,它们 5.Factor-→ Expr 恰好就是运算符‘*’的两个运 {$$=$2;} 算对象,所以,现在将‘*输 出到POST中是合适的。 6.liden=p; 最后,因POST[p]已被赋值 POST[p]=$1;p++; (即翻译所得的部分代码已输 出),应将下标计数加一
例:翻译表达式的S-属性文法 ⒈Expr→ Expr ‘+’ Term {$$=$1;POST[p]=‘+’; p++;} ⒉ | Term {$$=$1;} ⒊Term→ Term ’*’ Factor {$$=$1;POST[p] = ‘*’; p++;} ⒋ | Factor{$$=$1;} ⒌Factor→ ‘(‘ Expr ‘)’ { $$=$2;} ⒍ |iden{$$=p; POST[p] =$1; p++;} 我们以第3式为例介绍其原理。 首先,产生式左部Term的首地址显 然应与右部第一符号对应的首地 址相同($$=$1;)。 其次,按第3式归约时,或者说, 翻译文法执行该语义动作时,右 部符号Term和Factor对应的输出 (即各自所代表的代码段)已经 建立,并已存储在POST中,它们 恰好就是运算符‘*’的两个运 算对象,所以,现在将‘*’输 出到POST中是合适的。 最后,因POST[p]已被赋值 (即翻译所得的部分代码已输 出),应将下标计数加一
对A+B*C进行分析翻译的过程 步骤 分析栈 R 余留输 分析动作及归约所 后缀表 小N 0 # A 在钱# 避生式和子程年 1 #A B*C# 归约F→i,SUB6 A 2 #F + B*C# 归约T→F,SUB4 A 3 #T + B*C# 归约E→TSUB2 A 4 #E + B*C# 移进 A 5 #E+ B *C# 移进 A 6 #E+B C# 归约F→i,SUB6 AB 7 #E+F C# 归约T→F,SUB4 AB 8 #E+T C# 移进 AB 9 #E+T* C 为 移进 AB 10 #E+T* # 归约F→i,SUB6 ABC 11 #E+T*F 并 归约T→T*F,SUB3 ABC* 12 #E+T # 归约E→E+TSUB1 ABC* 13 #E ABC*+
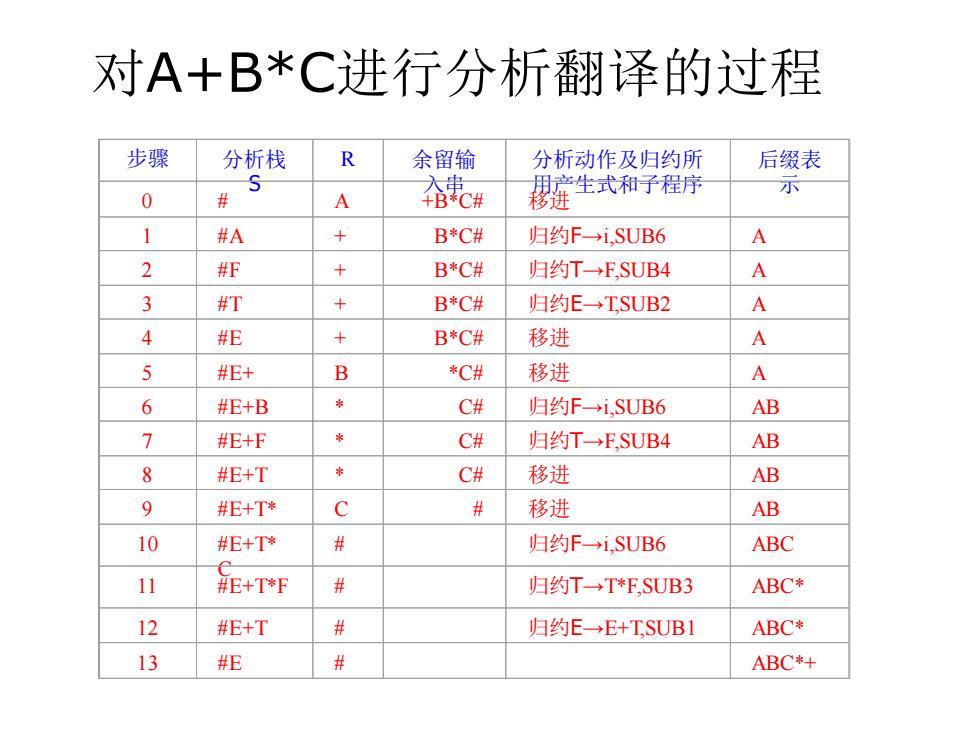
步骤 分析栈 S R 余留输 入串 分析动作及归约所 用产生式和子程序 后缀表 示 0 # A +B*C# 移进 1 #A + B*C# 归约F→i,SUB6 A 2 #F + B*C# 归约T→F,SUB4 A 3 #T + B*C# 归约E→T,SUB2 A 4 #E + B*C# 移进 A 5 #E+ B *C# 移进 A 6 #E+B * C# 归约F→i,SUB6 AB 7 #E+F * C# 归约T→F,SUB4 AB 8 #E+T * C# 移进 AB 9 #E+T* C # 移进 AB 10 #E+T* C # 归约F→i,SUB6 ABC 11 #E+T*F # 归约T→T*F,SUB3 ABC* 12 #E+T # 归约E→E+T,SUB1 ABC* 13 #E # ABC*+ 对A+B*C进行分析翻译的过程

5.3.2四元式和三元式 ·四元式是一种更接近目标代码的中间代码形式,由于这种 形式的中间代码便于优化处理,因此,在目前的许多编译 程序中得到了广泛的应用。 ·四元式是一种“三地址语句”的等价表示。它的一般形式 为:(op,arg1,arg2,result) 其中,op为一个二元(也可是一元或零元)运算符; arg1,arg2分别为它的两个运算对象,它们可以是变量、 常数或系统定义的临时变量名;运算的结果将放入result 中。四元式还可写为类似于PASCAL语言的赋值语句的形 式:result:=arg1 op arg2
5.3.2 四元式和三元式 • 四元式是一种更接近目标代码的中间代码形式,由于这种 形式的中间代码便于优化处理,因此,在目前的许多编译 程序中得到了广泛的应用。 • 四元式是一种“三地址语句”的等价表示。它的一般形式 为:(op,arg1,arg2,result) 其 中 , op 为一个二元 ( 也可是一元或零元 ) 运算符 ; arg1,arg2分别为它的两个运算对象,它们可以是变量、 常数或系统定义的临时变量名;运算的结果将放入result 中。四元式还可写为类似于PASCAL语言的赋值语句的形 式:result := arg1 op arg2

四元式的格式 需要指出的是,每个四元式只能有一个运算符,所以,一 个复杂的表达式只能由多个四元式构成的序列表示。 。 例如,表达式A+B*C可写为序列 T1:=B*C T2:=A+T1 ● 当op为一元、零元运算(如无条件转移)时,arg2甚至 arg1应缺省,即result:=op arg1或op result;对应 的一般形式为: (op,arg1,-,result) 或 (op,,,result)
四元式的格式 • 需要指出的是,每个四元式只能有一个运算符,所以,一 个复杂的表达式只能由多个四元式构成的序列表示。 • 例如,表达式A+B*C可写为序列 T1 :=B*C T2 :=A+T1 • 当op为一元、零元运算(如无条件转移)时,arg2甚至 arg1应缺省,即result:=op arg1或 op result ;对应 的一般形式为: (op,arg1,-,result) 或 (op,-,-,result)

三元式 为了节省临时变量的开销,有时也可采用一种三元式 结构来作为中间代码,其一般形式为 (i)(op,arg1,arg2) 其中,()为三元式的编号,也代表了该式的运算结果; op,arg1,arg2的含义与四元式类似,区别在于arg可 以是某三元式的序号,表示用该三元式的结果作为运 算对象。例如,对于赋值语句a:=-b*(c+d),若用三 元式表示,则可写成 ① (U_minus,b,- ② (+ c,d ③ (* ①,②) ④ (:=,③,a) 式①中的运算符U minus表示一元减运算
三元式 • 为了节省临时变量的开销,有时也可采用一种三元式 结构来作为中间代码,其一般形式为 (i) (op,arg1,arg2) 其中,(i)为三元式的编号,也代表了该式的运算结果; op,arg1,arg2的含义与四元式类似,区别在于arg可 以是某三元式的序号,表示用该三元式的结果作为运 算对象。例如,对于赋值语句a:=-b*(c+d),若用三 元式表示,则可写成 ① (U_minus, b, - ) ② ( + , c, d ) ③ ( * , ①, ② ) ④ ( := , ③, a ) 式①中的运算符U_minus表示一元减运算

翻译程序中使用的铺肋函数 ·我们以算术表达式到三元式的翻译为例,说明如何为各产 生式设计语义动作。为此,先介绍若干翻译过程中要使用 的辅助函数: l.int LookUp(char*Name)一以Name查符号表,若查到 则返回相应登记项的序号(≥1),否则返回0。 2.int Enter(char*Name)一以Name为名字在符号表中登 录新的一项,返回值为该项的序号。 3.int Entry(char*Name)一以Name为名字查、填符号表: int Entry(char *Name){int i=LookUp(Name); if(i)return i;else return Enter(Name);
翻译程序中使用的辅助函数 • 我们以算术表达式到三元式的翻译为例,说明如何为各产 生式设计语义动作。为此,先介绍若干翻译过程中要使用 的辅助函数: ⒈int LookUp(char *Name)—以Name查符号表,若查到 则返回相应登记项的序号(≥1),否则返回0。 ⒉int Enter(char* Name)—以Name为名字在符号表中登 录新的一项,返回值为该项的序号。 ⒊int Entry(char *Name)—以Name为名字查、填符号表: int Entry(char *Name){ int i=LookUp(Name); if(i) return i;else return Enter(Name); }