
China-pub.com 下载 第3章 上下文无关文法及分析 本章要点 ·分析过程 ·扩展的表示法:EBNF和语法图 ·上下文无关文法 ·上下文无关语言的形式特性 ·分析树与抽象语法树 ·TNY语言的语法 ·二义性 分析的任务是确定程序的语法,或称作结构,也正是这个原因,它又被称作语法分析 (syntax analysis)。程序设计语言的语法通常是由上下文无关(context--free grammar)的文法规 则(grammar rule)给出,其方式同扫描程序识别的由正则表达式提供的记号的词法结构相类 似。上下文无关文法的确利用了与正则表达式中极为类似的命名惯例和运算。二者的主要区别 在于上下文无关文法的规则是递归的(recursive)。例如一般来说,if语句的结构应允许可其中 嵌套其他的语句,而在正则表达式中却不能这样做。这个区别造成的影响很大。由上下文无 关文法识别的结构类比由正则表达式识别的结构类大大增多了。用作识别这些结构的算法也与 扫描算法差别很大,这是因为它们必须使用递归调用或显式管理的分析栈。用作表示语言语义 结构的数据结构现在也必须是递归的,而不再是线性的(如同用于词法和记号中的一样)了。 经常使用的基本结构是一类树,称作分析树(parse tree)或语法树(syntax tree). 同第2章相似,在学习分析算法和如何利用这些算法进行真正的分析之前需要先学习上下 文无关文法的理论,但是又与在扫描程序中的情形不同一一其中主要只有一种算法方法(表示 为有穷自动机),分析涉及到要在许多属性和能力截然不同的方法中做出选择。按照它们构造 分析树或语法树的方式,算法大致可分为两种:自顶向下分析(top-down parsing)和由底向 上分析(bottom-up parsing)。对这些分析方法的详细讨论将放到以后的章节中,本章只给出分 析过程的一般性描述,之后还要学习上下文无关文法的基础理论。最后一节则从一个上下文无 关文法的角度给出TNY语言的文法。对上下文无关文法理论和语法树熟悉的读者可以跳过本 章中间的某些内容(或将其作为复习)。 3.1分析过程 分析程序的任务是从由扫描程序产生的记号中确定程序的语法结构,以及或隐式或显式地 构造出表示该结构的分析树或语法树。因此,可将分析程序看作一个函数,该函数把由扫描程 序生成的记号序列作为输入,并生成语法树作为它的输出: 记号序列分析程序、酒法树 记号序列通常不是显式输入参数,但是当分析过程需要下一个记号时,分析程序就调用诸如 getToken的扫描程序过程以从输入中获得它。因此,编译器的分析步骤可减为对分析程序的 个调用,如下所示: syntaxTree parse (
下载 第3章 上下文无关文法及分析 本章要点 • 分析过程 • 扩展的表示法:E B N F和语法图 • 上下文无关文法 • 上下文无关语言的形式特性 • 分析树与抽象语法树 • TINY语言的语法 • 二义性 分析的任务是确定程序的语法,或称作结构,也正是这个原因,它又被称作语法分析 (syntax analysis)。程序设计语言的语法通常是由上下文无关( context-free grammar)的文法规 则(grammar rule)给出,其方式同扫描程序识别的由正则表达式提供的记号的词法结构相类 似。上下文无关文法的确利用了与正则表达式中极为类似的命名惯例和运算。二者的主要区别 在于上下文无关文法的规则是递归的(r e c u r s i v e)。例如一般来说,if 语句的结构应允许可其中 嵌套其他的i f语句,而在正则表达式中却不能这样做。这个区别造成的影响很大。由上下文无 关文法识别的结构类比由正则表达式识别的结构类大大增多了。用作识别这些结构的算法也与 扫描算法差别很大,这是因为它们必须使用递归调用或显式管理的分析栈。用作表示语言语义 结构的数据结构现在也必须是递归的,而不再是线性的(如同用于词法和记号中的一样)了。 经常使用的基本结构是一类树,称作分析树(parse tree)或语法树(syntax tree)。 同第2章相似,在学习分析算法和如何利用这些算法进行真正的分析之前需要先学习上下 文无关文法的理论,但是又与在扫描程序中的情形不同——其中主要只有一种算法方法(表示 为有穷自动机),分析涉及到要在许多属性和能力截然不同的方法中做出选择。按照它们构造 分析树或语法树的方式,算法大致可分为两种:自顶向下分析( top-down parsing)和由底向 上分析(bottom-up parsing)。对这些分析方法的详细讨论将放到以后的章节中,本章只给出分 析过程的一般性描述,之后还要学习上下文无关文法的基础理论。最后一节则从一个上下文无 关文法的角度给出T I N Y语言的文法。对上下文无关文法理论和语法树熟悉的读者可以跳过本 章中间的某些内容(或将其作为复习)。 3.1 分析过程 分析程序的任务是从由扫描程序产生的记号中确定程序的语法结构,以及或隐式或显式地 构造出表示该结构的分析树或语法树。因此,可将分析程序看作一个函数,该函数把由扫描程 序生成的记号序列作为输入,并生成语法树作为它的输出: 记号序列 语法树 记号序列通常不是显式输入参数,但是当分析过程需要下一个记号时,分析程序就调用诸如 g e t T o k e n的扫描程序过程以从输入中获得它。因此,编译器的分析步骤可减为对分析程序的 一个调用,如下所示: syntaxTree = parse(); 分析程序

70 翁译原理及实践 China-pub.co 下载 在单遍编译中,分析程序合并编译器中所有的其他阶段,这还包括了代码生成,因此也就 不需要构造显式的语法树了(分析步骤本身隐式地表示了语法树),由此就发生了一个 parse(): 调用。在编译器中更多的是多遍,此时后面的遍将语法树作为它们的输入。 语法树的结构在很大程度上依赖于语言特定的语法结构。这种树通常被定义为动态数据结 构,该结构中的每个节点都由一个记录组成,而这个记录的域包括了编译后面过程所需的特性 (即:并不是那些由分析程序计算的特性)。节点结构通常是节省空间的各种记录。特性域还可 以是在需要时动态分配的结构,它就像一个更进一步节省空间的工具。 在分析程序中有一个比在扫描程序中更为复杂的问题,这就是对于错误的处理。在扫描程 序中,如果遇到的一个字符是不正规记号的一部分,那么它只需生成一个出错记号并消耗掉这 个讨厌的字符即可(在某种意义上,通过生成一个出错记号,扫描程序就克服了发生在分析程 序上的困难)。但对于分析程序而言,它必须不仅报告一个出错信息,而且还须从错误状态恢 复(recover)并继续进行分析(去找到尽可能多的错误)。分析程序有时会执行错误修复 尽可能接近真正错误时继续分析下去。由于要到错误真正地已经发生了分析程序才会发现它, 所以做到这一点并不简单。由于错误恢复技术依赖于所使用的特定分析算法,所以本章先就不 学习它了。 3.2上下文无关文法 上下文无关文法说明程序设计语言的语法结构。除了上下文无关文法涉及到了递归规则之 外,这样的说明与使用正则表达式的词法结构的说明十分类似。例如在一个运算中,就可以使 用带有加法、减法和乘法的简单整型算术表达式。这些表达式可由下面的文法给出 exp-exp op expl (exp)I number 叩+1-1* 3.2.1与正则表达式比较 在第2章中为number?给出的正则表达式规则如下所示 number=digit digit d1g1t=0111213141516171819 试与上面上下文无关文法的样本作一比较。基本正则表达式规则有3种运算:选择(由竖 线元字符表示)、并置(不带元符号)以及重复(由星号元符号提供)。此外还可用等号来表示 正则表达式的名字定义,此时名字用斜体书写以示与真正字符序列的区别。 文法规则使用相似的表示法。名字用斜体表示(但它是一种不同的字体,所以可与正则表 达式相区分)。竖线仍表示作为选择的元符号。并置也用作一种标准运算。但是这里没有重复 的元符号(如正则表达式中的星号◆),稍后还会再讲到它。表示法中的另一个差别是现在用箭 头符号“一”代替了等号来表示名字的定义。这是由于现在的名字不能简单地由其定义取代, 而需要更为复杂的定义过程来表示,这是由定义的递归本质决定的⊙。在我们的示例中,x即的 日参见本章后面的语法规则和等式
在单遍编译中,分析程序合并编译器中所有的其他阶段,这还包括了代码生成,因此也就 不需要构造显式的语法树了(分析步骤本身隐式地表示了语法树),由此就发生了一个 p a r s e ( ) ; 调用。在编译器中更多的是多遍,此时后面的遍将语法树作为它们的输入。 语法树的结构在很大程度上依赖于语言特定的语法结构。这种树通常被定义为动态数据结 构,该结构中的每个节点都由一个记录组成,而这个记录的域包括了编译后面过程所需的特性 (即:并不是那些由分析程序计算的特性)。节点结构通常是节省空间的各种记录。特性域还可 以是在需要时动态分配的结构,它就像一个更进一步节省空间的工具。 在分析程序中有一个比在扫描程序中更为复杂的问题,这就是对于错误的处理。在扫描程 序中,如果遇到的一个字符是不正规记号的一部分,那么它只需生成一个出错记号并消耗掉这 个讨厌的字符即可(在某种意义上,通过生成一个出错记号,扫描程序就克服了发生在分析程 序上的困难)。但对于分析程序而言,它必须不仅报告一个出错信息,而且还须从错误状态恢 复( r e c o v e r)并继续进行分析(去找到尽可能多的错误)。分析程序有时会执行错误修复 (error repair),此时它从提交给它的非正确的版本中推断出一个可能正确的代码版本(这通常 是在简单情况下才发生的)。错误恢复的一个尤为重要的方面是有意义的错误信息报告以及在 尽可能接近真正错误时继续分析下去。由于要到错误真正地已经发生了分析程序才会发现它, 所以做到这一点并不简单。由于错误恢复技术依赖于所使用的特定分析算法,所以本章先就不 学习它了。 3.2 上下文无关文法 上下文无关文法说明程序设计语言的语法结构。除了上下文无关文法涉及到了递归规则之 外,这样的说明与使用正则表达式的词法结构的说明十分类似。例如在一个运算中,就可以使 用带有加法、减法和乘法的简单整型算术表达式。这些表达式可由下面的文法给出: e x p→exp op exp | (e x p) | n u m b e r op → + | - | * 3.2.1 与正则表达式比较 在第2章中为n u m b e r给出的正则表达式规则如下所示: number = digit digit* digit = 0|1|2|3|4|5|6|7|8|9 试与上面上下文无关文法的样本作一比较。基本正则表达式规则有 3种运算:选择(由竖 线元字符表示)、并置(不带元符号)以及重复(由星号元符号提供)。此外还可用等号来表示 正则表达式的名字定义,此时名字用斜体书写以示与真正字符序列的区别。 文法规则使用相似的表示法。名字用斜体表示(但它是一种不同的字体,所以可与正则表 达式相区分)。竖线仍表示作为选择的元符号。并置也用作一种标准运算。但是这里没有重复 的元符号(如正则表达式中的星号*),稍后还会再讲到它。表示法中的另一个差别是现在用箭 头符号“→”代替了等号来表示名字的定义。这是由于现在的名字不能简单地由其定义取代, 而需要更为复杂的定义过程来表示,这是由定义的递归本质决定的 。在我们的示例中,e x p的 7 0 编译原理及实践 下载 参见本章后面的语法规则和等式

China-pub.Com 71 下载上 第3章上下文无关文法及分析 规则是递归的,其中名字cxp出现在箭头的右边 读者还要注意到文法规则将正则表达式作为部件。在xp规则和op规则中,实际有6个表示 语言中记号的正则表达式。其中5个是单字符记号:+、-、*、(和),另一个是名字number 记号的名字表示数字序列。 与这个例子的格式相类似的文法规则最初是用在A1go60语言的描述中。其表示法是由 John Backus为Algole6O报告开发,之后又由Peter Naur更新,因此这个格式中的文法通常被称作 Backus-Naur范式(Backus-Naur form)或BNE文法. 3.2.2上下文无关文法规则的说明 同正则表达式类似,文法规则是定义在一个字母表或符号集之上。在正则表达式中,这些 符号通常就是字符,而在文法规则中,符号通常是表示字符串的记号。在前一章中,我们利用 C中的枚举类型定义了在扫描程序中的记号:本章为了避免涉及到特定实现语言(例如C)中 表示记号的细节,就使用了正则表达式本身来表示记号。此时的记号就是一个固定的符号,如 同在保留字w11。中或诸如+或:=这样的特殊符号一样,使用在第2章曾用到的代码字体书写 串本身。对于作为表示多于 一个串的标识符和数的记号来说,代码字体为斜体,这就同假设这 个记号是正则表达式的名字(这是它经常的表示)一样。例如,将TNY语言的记号字母表表 示为集合 (if,then,else,end,repeat,until,read,write. identifier,number,+,-,./=,并将原来斜体的记号名字大写:因此,使用不同的惯例,上面的文法规则就可 变为: :=I I NUMBER ::=+1-1t 每一个作者都还有这些表示法的其他变形。本节后面将会谈到一些非常重要的变形(其中
规则是递归的,其中名字e x p出现在箭头的右边。 读者还要注意到文法规则将正则表达式作为部件。在 e x p规则和o p规则中,实际有6个表示 语言中记号的正则表达式。其中5个是单字符记号:+、-、*、( 和 ),另一个是名字n u m b e r。 记号的名字表示数字序列。 与这个例子的格式相类似的文法规则最初是用在 A l g o l 6 0语言的描述中。其表示法是由 John Backus为A l g o l 6 0报告开发,之后又由Peter Naur更新,因此这个格式中的文法通常被称作 B a c k u s - N a u r范式(Backus-Naur form)或B N F文法。 3.2.2 上下文无关文法规则的说明 同正则表达式类似,文法规则是定义在一个字母表或符号集之上。在正则表达式中,这些 符号通常就是字符,而在文法规则中,符号通常是表示字符串的记号。在前一章中,我们利用 C中的枚举类型定义了在扫描程序中的记号;本章为了避免涉及到特定实现语言(例如 C)中 表示记号的细节,就使用了正则表达式本身来表示记号。此时的记号就是一个固定的符号,如 同在保留字w h i l e中或诸如+或: =这样的特殊符号一样,使用在第 2章曾用到的代码字体书写 串本身。对于作为表示多于一个串的标识符和数的记号来说,代码字体为斜体,这就同假设这 个记号是正则表达式的名字(这是它经常的表示)一样。例如,将 T I N Y语言的记号字母表表 示为集合 {if, then, else, end, repeat, until, read, write, i d e n t i f i e r, n u m b e r, +, -, *, /, =, 并将原来斜体的记号名字大写;因此,使用不同的惯例,上面的文法规则就可 变为: ::= | ( ) | NUMBER ::= + | - | * 每一个作者都还有这些表示法的其他变形。本节后面将会谈到一些非常重要的变形(其中 第 3章 上下文无关文法及分析 7 1 下载

72 翁译原理及实践 China-pub.Co 下载 一些有时也会碰到)。这里要先讲一下有关表示法方面的另外两个较小的问题。 在BNF的元符号中使用括号有时很有用,这同括号可在正则表达式中重新安排优先权很相 似。例如,可将上面的文法规则重写为如下一个单一的文法规则: exp-exp("+"""")exp"("exp")"I number 在这个规则中,括号很必要,它用于将箭头右边的表达式之间的算符选择组合在一起,这 是因为并置优先于选择(同在正则表达式中一样)。因此,下面的规则就具有了不同(但不正 确)的含义: exp-exp"+"""*"exp"("exp")"I number 请读者再留意一下:当将括号包含为一个元符号时,就有必要区分括号记号与元符号,这 一点是通过将括号记号放在引号中做到的,这同在正则表达式中的一样(为了具有连贯性,也 将算符符号放在引号中)。 由于经常可将括号中的部分分隔成新的文法规测,所以在BNF中的括号并不像元符号一样 缺之不可。实际上如果允许在箭头左边的相同名字可出现任意次,那么由竖线元符号给出的选 择运算在文法规则中也不是一定要有的。例如,简单的表达式文法可写作: ep→exp op exp ep→(exp) exp→number p→- 然而,通常把文法规则写成每个结构的所有选择都可在一个规则中列出来,而且每个结构 名字在箭头左边只出现一次。 有时我们需要为说明简便性而给出一些用简短表示法写出的文法规则的示例。在这些情形 中,应将结构名字大写,并小写单个的记号符号(它们经常仅仅是一个字符);因此,按这种 速记方法可将简单的表达式文法写作: E→EOEI(E)In O++|-* 有时当正在将字符如同记号一样使用时,且无需使用代码字体来书写它们,则也可简化表 示法如下: E→EOEI(E)la 0一+1-1 3.2.3推导及由文法定义的语言 现在讨论文法规则如何确定一种“语言”或者是记号的正规串集。 下文无关文法规则确定了为由规则定义的结构的记号符号符合语法的串集。例如,算术 表达式 (34-3)★42 与7个记号的正规串相对应 number-number)*number 其中aumberi记号具有由扫描程序确定的结构且串本身也是一个正规的表达式,这是因为
一些有时也会碰到)。这里要先讲一下有关表示法方面的另外两个较小的问题。 在B N F的元符号中使用括号有时很有用,这同括号可在正则表达式中重新安排优先权很相 似。例如,可将上面的文法规则重写为如下一个单一的文法规则: exp → exp ( "+" | "-" | "*") exp | "("e x p")" | n u m b e r 在这个规则中,括号很必要,它用于将箭头右边的表达式之间的算符选择组合在一起,这 是因为并置优先于选择(同在正则表达式中一样)。因此,下面的规则就具有了不同(但不正 确)的含义: exp → exp "+" | "-" | "*" exp | "("e x p")" | n u m b e r 请读者再留意一下:当将括号包含为一个元符号时,就有必要区分括号记号与元符号,这 一点是通过将括号记号放在引号中做到的,这同在正则表达式中的一样(为了具有连贯性,也 将算符符号放在引号中)。 由于经常可将括号中的部分分隔成新的文法规则,所以在 B N F中的括号并不像元符号一样 缺之不可。实际上如果允许在箭头左边的相同名字可出现任意次,那么由竖线元符号给出的选 择运算在文法规则中也不是一定要有的。例如,简单的表达式文法可写作: exp → exp op exp exp → (e x p) exp → n u m b e r op → + op → - op → * 然而,通常把文法规则写成每个结构的所有选择都可在一个规则中列出来,而且每个结构 名字在箭头左边只出现一次。 有时我们需要为说明简便性而给出一些用简短表示法写出的文法规则的示例。在这些情形 中,应将结构名字大写,并小写单个的记号符号(它们经常仅仅是一个字符);因此,按这种 速记方法可将简单的表达式文法写作: E → E O E|( E ) | n O → + | - | * 有时当正在将字符如同记号一样使用时,且无需使用代码字体来书写它们,则也可简化表 示法如下: E → E O E|( E ) | a O → + | - | * 3.2.3 推导及由文法定义的语言 现在讨论文法规则如何确定一种“语言”或者是记号的正规串集。 上下文无关文法规则确定了为由规则定义的结构的记号符号符合语法的串集。例如,算术 表达式 ( 3 4 - 3 ) * 4 2 与7个记号的正规串相对应 ( number - number ) * n u m b e r 其中n u m b e r记号具有由扫描程序确定的结构且串本身也是一个正规的表达式,这是因为 7 2 编译原理及实践 下载

China-pub.Com 第3章上下文无关文法及分析 73 下载H 每一个部分都与由文法规则 exp-exp op expl (exp)number 一+1-1* 给出的选择对应。另一方面,串 (34-3*42 就不是正规的表达式,这是因为左括号没有一个右括号与之匹配,且xp的文法规则中的 第2个选择要求括号需成对生成。 文法规则通过推导确定记号符号的正规串。推导(derivation)是在文法规则的右边进行选 择的一个结构名字替换序列。推导以一个结构名字开始并以记号符号串结束。在推导的每一个 步骤中,使用来自文法规则的选择每一次生成一个替换。 例如,图3-1利用同在上面简单表达式文法中的一样给出的文法规则为表达式(34-3)*42 提供了一个推导。在每一步中,为替换所用的文法规则选择都放在了右边(还为便于在后面引 用为每一步都编了号)。 ()ep→exp op e ep→exp op exp] →exp op number [ep→aumber】 →exp*number [op→t1 (4) →《en】曹number [ep→(ep)】 →(exp op exp)*aumber [ep→exp op exp →(exp op nu er)*number [ep-→number】 (7) 一(exp-number)number (8) (number-number)*number [ep→number】 图3-1算术表达式34-3)*2的推导 请注意,推导步骤使用了与文法规则中的箭头元符号不同的箭头,这是由于推导步骤与文 法规则有一点差别:文法规则定义(define),而推导步骤却通过替换来构造(construct)。在 图3-1的第1步中,串exp op exp从规则cxp一exp op exp的(在BNF中对于exp的第1个选择)右 边替换了单个的exp。在第2步中,串exp op exp中的exp被符号number从选择exp一number的 右边替换掉以得到串exp op number。在第3步中,符号*从规则op→*中替换op(在BNF中对 于op的第3个选择)以得到串exp*number,等等。 由推导从cxp符号中得到的所有记号符号的串集是被表达式的文法定义的语言(language defined by the grammar)。这个语言包括了所有合乎语法的表达式。可将它用符号表示为: L(G={slp*s} 其中G代表表达式文法,s代表记号符号的任意数组串(有时称为句子(sentence),而符 号一*表示由如前所述的替换序列组成的推导(星号用作指示步骤的序列,这与在正则表达式 中指示重复很相像)。由于它们通过推导“产生”L(G)中的串,文法规则因此有时也称作 生式(production)。 文法中的每一个结构名定义了符合语法的记号串的自身语言。例如,在简单表达式文法中 由叩定义的语言定义了语言(+,-,*)只由3个符号组成。我们通常对由文法中最普通的结 构定义的语言最感兴趣。用于程序设计语言的文法经常定义一个称作程序的结构,而该结构的 语言是程序设计语言的所有符合语法的程序的集合(注意这里在两个不同的意思中所使用的 “语言”)
每一个部分都与由文法规则 exp → exp op exp | (e x p) | n u m b e r op → + | - | * 给出的选择对应。另一方面,串 ( 3 4 - 3 * 4 2 就不是正规的表达式,这是因为左括号没有一个右括号与之匹配,且 e x p的文法规则中的 第2个选择要求括号需成对生成。 文法规则通过推导确定记号符号的正规串。推导( d e r i v a t i o n)是在文法规则的右边进行选 择的一个结构名字替换序列。推导以一个结构名字开始并以记号符号串结束。在推导的每一个 步骤中,使用来自文法规则的选择每一次生成一个替换。 例如,图3 - 1利用同在上面简单表达式文法中的一样给出的文法规则为表达式 ( 3 4 - 3 ) * 4 2 提供了一个推导。在每一步中,为替换所用的文法规则选择都放在了右边(还为便于在后面引 用为每一步都编了号)。 图3-1 算术表达式( 3 4 - 3 ) * 4 2 的推导 请注意,推导步骤使用了与文法规则中的箭头元符号不同的箭头,这是由于推导步骤与文 法规则有一点差别:文法规则定义( d e f i n e),而推导步骤却通过替换来构造( c o n s t r u c t)。在 图3 - 1的第1步中,串exp op exp从规则e x p→exp op exp的(在B N F中对于e x p的第1个选择)右 边替换了单个的e x p。在第2步中,串exp op exp中的e x p被符号n u m b e r从选择e x p→n u m b e r的 右边替换掉以得到串exp op n u m b e r。在第3步中,符号*从规则o p→*中替换o p(在B N F中对 于o p的第3个选择)以得到串exp * n u m b e r,等等。 由推导从e x p符号中得到的所有记号符号的串集是被表达式的文法定义的语言( l a n g u a g e defined by the grammar)。这个语言包括了所有合乎语法的表达式。可将它用符号表示为: L (G) = {s | exp Þ *s } 其中G代表表达式文法,s 代表记号符号的任意数组串(有时称为句子( s e n t e n c e)),而符 号Þ*表示由如前所述的替换序列组成的推导(星号用作指示步骤的序列,这与在正则表达式 中指示重复很相像)。由于它们通过推导“产生” L (G)中的串,文法规则因此有时也称作产 生式(p r o d u c t i o n)。 文法中的每一个结构名定义了符合语法的记号串的自身语言。例如,在简单表达式文法中 由op 定义的语言定义了语言{+, -, *}只由3个符号组成。我们通常对由文法中最普通的结 构定义的语言最感兴趣。用于程序设计语言的文法经常定义一个称作程序的结构,而该结构的 语言是程序设计语言的所有符合语法的程序的集合(注意这里在两个不同的意思中所使用的 “语言”)。 第 3章 上下文无关文法及分析 7 3 下载

74 翁译原理及实践 China-pub.co 下载 例如:Pascal的BNF以诸如 program -program-heading program-block. program-heading→. program-block→ 的文法规则开始(第1个规则认为程序由一个程序头、随后的分号、随后的程序块,以及位于 最后的一个句号组成)。在诸如C的带有独立编译的语言中,最普通的结构通常称作编译单元。 除非特别指出不是,在各种情况下都假定在文法规则中,第1个列出的就是这个最普通的结检 (在上下文无关文法的数学理论中,这个结构称作开始符号(start symbol)。 通过更深一些的术语可更清楚地区分结构名和字母表中的符号(因为它们经常是编译应用 程序的记号,所以我们一直调用记号符号)。由于在推导中必须被进一步替换(它们不终结推 导),所以结构名也称作非终结符(nonterminal)。相反地,由于字母表中的符号终结推导,所 以它们被称作终结符(terminal)。因为终结符通常是编译应用程序中的记号,所以这两个名字 在使用时是基本同义的。终结符和非终结符经常都被认作是符号 下面是一些由文法生成的语言示例。 例3.1考虑带有单个文法规则的文法G E-(E)a 这个文法有1个非终结符E、3个终结符()以及a。这个文法生成语言(G)={a,(a),(a), ((a)}={(a)|n是一个≥0的整型},即:串由零个或多个左括号、后接一个a,以及后面 是与左括号相同数量的右括号组成。作为这些串的一个推导示例,我们给出()的一个推导: E→(E)→(E)→(a) 例3.2考虑带有单个文法规则 E+(E) 的文法G。除了减少了洗项E·之外,这是与前例相同的文法。这个文法根本就不生成串,因 此它的语言是空的:L(G={}。其原因在于任何以E开头的推导都生成总是含有E的串,所以 没有办法推导出一个仅包含有终结符的串。实际上,与带有所有递归进程(如归纳论证或递归 函数)相同,递归地定义一个结构的文法规则必须总是有至少一个非递归情况(称之为基础情 况(base case)。本例中的文法并没有这样的情况,且任何潜在的推导都注定为无穷递归。 例3.3考虑带有单个文法规则 E-E+al a 的文法G。这个文法生成所有由若干个“+”分隔开的a组成的串 L(G)={a,a+a,a+a+a,a+a+a+a,... 为了(非正式地)查看它,可考虑规则E→E+a的效果:它引起串+a在推导右边不断地重复: EE+a→E+a+a→E+a+a+a→. 最后,必须用基础情况E一a来替换左边的E。 若要更正式一些,则可如下来归纳证明:首先,通过归纳a的数目来表示每个串a+a+ +a都在L(G中。推导E→a表示a在L(G)中:现在假设s=a+a++a在L(G中,且有m广1 个a,则存在推导E一*s。现在推导E一E+a一*s+a表示串s+a在L(G)中,且其中有n个a。 相反地,我们也表示出在L(G中的任何串s都必须属于格式a+a+ +a。这是通过归纳推导
例如:P a s c a l的B N F以诸如 p rogram → p rogram-heading ; p ro g r a m - b l o c k. p rogram-heading → . . . p rogram-block → . . . . . . 的文法规则开始(第 1个规则认为程序由一个程序头、随后的分号、随后的程序块,以及位于 最后的一个句号组成)。在诸如C的带有独立编译的语言中,最普通的结构通常称作编译单元。 除非特别指出不是,在各种情况下都假定在文法规则中,第 1个列出的就是这个最普通的结构 (在上下文无关文法的数学理论中,这个结构称作开始符号( start symbol))。 通过更深一些的术语可更清楚地区分结构名和字母表中的符号(因为它们经常是编译应用 程序的记号,所以我们一直调用记号符号)。由于在推导中必须被进一步替换(它们不终结推 导),所以结构名也称作非终结符(n o n t e r m i n a l)。相反地,由于字母表中的符号终结推导,所 以它们被称作终结符(t e r m i n a l)。因为终结符通常是编译应用程序中的记号,所以这两个名字 在使用时是基本同义的。终结符和非终结符经常都被认作是符号。 下面是一些由文法生成的语言示例。 例3.1 考虑带有单个文法规则的文法G E→(E)|a 这个文法有1个非终结符E、3个终结符(,) 以及a。这个文法生成语言 L(G) = {a, (a), ((a) ) , ( ( (a))),...} = {(n a) n | n 是一个≥0的整型 },即:串由零个或多个左括号、后接一个a,以及后面 是与左括号相同数量的右括号组成。作为这些串的一个推导示例,我们给出 ( (a) )的一个推导: E Þ (E) Þ ( (E)) Þ ( (a) ) 例3.2 考虑带有单个文法规则 E→(E) 的文法G。除了减少了选项E→a之外,这是与前例相同的文法。这个文法根本就不生成串,因 此它的语言是空的:L(G) = { }。其原因在于任何以E开头的推导都生成总是含有E的串,所以 没有办法推导出一个仅包含有终结符的串。实际上,与带有所有递归进程(如归纳论证或递归 函数)相同,递归地定义一个结构的文法规则必须总是有至少一个非递归情况(称之为基础情 况(base case))。本例中的文法并没有这样的情况,且任何潜在的推导都注定为无穷递归。 例3.3 考虑带有单个文法规则 E→E + a|a 的文法G。这个文法生成所有由若干个“+”分隔开的a 组成的串: L(G) = { a, a + a, a + a + a, a + a + a + a, . . . } 为了(非正式地)查看它,可考虑规则E→E + a 的效果:它引起串 + a 在推导右边不断地重复: E Þ E + a Þ E + a + a Þ E + a + a + a Þ . . . 最后,必须用基础情况E→a 来替换左边的E。 若要更正式一些,则可如下来归纳证明:首先,通过归纳 a 的数目来表示每个串a + a + . .. + a 都在L(G)中。推导E Þ a 表示a 在L(G) 中;现在假设s = a + a + ... + a 在L(G) 中,且有n-1 个a,则存在推导E Þ* s。现在推导E Þ E + a Þ *s + a 表示串s + a 在L(G)中,且其中有n 个a。 相反地,我们也表示出在L(G) 中的任何串s 都必须属于格式a + a + ... + a。这是通过归纳推导 7 4 编译原理及实践 下载

China-pub.Com 75 下载上 第3章上下文无关文法及分析 的长度得出的。假设推导的长度为1,则它属于格式E一,而且s是正确格式。现在假设以下 两个推导都为真:所有串都带有长度为一1的推导,并使E三*5是长度为n>1的推导:则这个 推导开头必须将E改为E+a,格式E三E+a三s'+a=s也是这样。则s'有长度为m1的推导, 格式a+a+…+a也是这样:因此,s本身必须也具有这个相同的格式。 例3.4考虑下面语句的极为简化的文法: statement if-stmt other if-simt-if (exp)statement i (exp)statemen else statement exn011 这个文法的语言包括位于类似C的格式中的嵌套i语句(我们已将逻辑测试表达式简化为0或1, 且除if语句外的所有语句都被放在终结符other中了)。例如,这个语言中的串是: 。ha e0 othe。 1Et1)。hex if 0 other else other if 1 other else other if 0 if 0 other if (0 if 1 other else other if 1 other else if 0 other else other 请注意,if语句中的可选else部分由用于if-stmt的文法规则中的单个选择指出。 在前面我们已注意到:BNF中的文法规则规定了并置和选择,但不具有与正则表达式的 相等同的特定重复运算。由于可由递归得到重复,所以这样的运算实际并不必要(如同在功能 语言中的程序员所知道的)。例如,文法规则 A-Aala 或文法规则 A→aAla 都生成语言{aIn是≥1的整型}(具有1个或多个a的所有串的集合),该语言与由正则表达式 a+生成的语言相同。例如,串aaaa可由带有推导 A→Aa→Aaa→Aaaa=aaaa 的第1个文法规则生成。一个类似的推导在第2个文法规则中起作用。由于非终结符A作为定义 A的规则左边的第1个符号出现,所以这些文法中的第1个是左递归(left recursive)9,第2个文 法则是右递归(right recursive).。 例33是左递归文法规则的另一个示例,它引出串“+”的重复。可将本例及前一个示例 归纳如下。考虑一个规则形式 A-AdB 其中a和B代表任意串,且B不以4开头。这个规则生成形式B、Ba、Baa、Baaa、的所有 串(所有串均以B开头,其后是零个或多个()。因此,这个文法规则在效果上与正则表达式 Bα*相同。类似地,右递归文法规则 A→a4IB 日这是左递归中的特珠情况,称作直接左递归(immediate).下一章将讨论一些更普通的情况
的长度得出的。假设推导的长度为1,则它属于格式E Þ a,而且s 是正确格式。现在假设以下 两个推导都为真:所有串都带有长度为 n-1的推导,并使E Þ* s 是长度为n > 1的推导;则这个 推导开头必须将E改为E +a,格式E Þ E + a Þ*s’ + a = s 也是这样。则s’有长度为n-1的推导, 格式a + a + ... + a 也是这样;因此,s 本身必须也具有这个相同的格式。 例3.4 考虑下面语句的极为简化的文法: statement → if-stmt | o t h e r if-stmt → if (e x p) s t a t e m e n t | if (e x p) statement e l s e s t a t e m e n t exp → 0 | 1 这个文法的语言包括位于类似 C的格式中的嵌套i f语句(我们已将逻辑测试表达式简化为 0或1, 且除i f语句外的所有语句都被放在终结符o t h e r中了)。例如,这个语言中的串是: o t h e r if ( 0 ) other if ( 1 ) other if ( 0 ) other else other if ( 1 ) other else other if ( 0 ) if ( 0 ) other if ( 0 ) if ( 1 ) other else other if ( 1 ) other else if ( 0 ) other else other . . . 请注意,if 语句中的可选else 部分由用于if-stmt 的文法规则中的单个选择指出。 在前面我们已注意到: B N F中的文法规则规定了并置和选择,但不具有与正则表达式的 * 相等同的特定重复运算。由于可由递归得到重复,所以这样的运算实际并不必要(如同在功能 语言中的程序员所知道的)。例如,文法规则 A → Aa | a 或文法规则 A → aA | a 都生成语言{a n | n 是≥1的整型}(具有1个或多个a 的所有串的集合),该语言与由正则表达式 a +生成的语言相同。例如,串aaaa 可由带有推导 A Þ Aa Þ Aaa Þ Aaaa Þ a a a a 的第1个文法规则生成。一个类似的推导在第 2个文法规则中起作用。由于非终结符 A作为定义 A的规则左边的第1个符号出现,所以这些文法中的第1个是左递归(left recursive) ,第2个文 法则是右递归(right recursive)。 例3 . 3是左递归文法规则的另一个示例,它引出串“ +a”的重复。可将本例及前一个示例 归纳如下。考虑一个规则形式 A→Aa|b 其中a 和b 代表任意串,且b 不以A开头。这个规则生成形式b、b a、b a a、b a a a、. . . .. . .的所有 串(所有串均以 b开头,其后是零个或多个 a)。因此,这个文法规则在效果上与正则表达式 b a*相同。类似地,右递归文法规则 A→aA|b 第 3章 上下文无关文法及分析 7 5 下载 这是左递归中的特殊情况,称作直接左递归( immediate left recursion),下一章将讨论一些更普通的情况

76 翁译原理及实践 China-pub.C 下载 (其中B并不在A处结束)生成所有串B、a邱、a邱、aa邓、 如果要编写生成与正则表达式a*相同语言的文法,则文法规则必须有一个用于生成空串 的的表示法(因为正则表达式ā*匹配空串)。这样的文法规则的右边必须为空,可在右边什么 也不写,如在 empry 中,但大多数情况都使用ε元符号表示空串(与在正则表达式中的用法类似): emp→e 这样的文法规则称作g-产生式(e-production)。生成包括了空串的文法必须至少有一个e-产 生式。 现在可以将一个与正则表达式a*相等的文法写作 A-Aa|ε 或 A-aA 8 两个文法都生成语言{a|n是≥0的整型}=L(a*)。-产生式在定义可选的结构时也很有 用,我们马上就能看到这一点。 下面用更多的一些示例来小结这个部分。 例3.5考虑文法 A→(A)AIE 这个文法生成所有“配对的括号”的串。例如,串()())()就由下面的推导生成(利用ε-产 生式去除无用的A): A=(A)A=(A)(A)A三(A)(A)三(A)()三(A)A)() ()A)()=()(A)A)()=()(A》() 三()(A)A》()=())A》()三)()》() 例3.6例3.4中的语句文法用e-产生式还可写作: statement-ifstmt l other if-stmtif exp)statement else-part else-part else statement e ep011 请注意,e-产生式指出结构else parti是可选的。 例3.7考虑一个语句序列的以下文法G: stmt-sequencestmt;stmt-sequence stmt stmt -s 这个文法生成由分号分隔开的一个或多个语句序列(语句已被提练到单个终结符s中了): L(G)={s,8;3,s;s:s,..} 如要允许语句序列也可为空,则可写出以下的文法G: stmt-sequencestmt;stmt-sequence stmte 但是它将分号变为一个语句结束符号(terminator)而不是分隔符(separator): L(G)={E,s;,s:s;,s:s:s:,..1
(其中b并不在A处结束)生成所有串b、a b、a a b、a aab、. . . . . . 如果要编写生成与正则表达式 a *相同语言的文法,则文法规则必须有一个用于生成空串 的的表示法(因为正则表达式 a *匹配空串)。这样的文法规则的右边必须为空,可在右边什么 也不写,如在 empty → 中,但大多数情况都使用 元符号表示空串(与在正则表达式中的用法类似): empty → 这样的文法规则称作 - 产生式( -p r o d u c t i o n)。生成包括了空串的文法必须至少有一个 -产 生式。 现在可以将一个与正则表达式a *相等的文法写作 A→A a| 或 A→a A| 两个文法都生成语言{a n | n 是≥0的整型} = L (a *)。 -产生式在定义可选的结构时也很有 用,我们马上就能看到这一点。 下面用更多的一些示例来小结这个部分。 例3.5 考虑文法 A→ (A) A| 这个文法生成所有“配对的括号”的串。例如,串 (( ) (( ))) ( )就由下面的推导生成(利用 -产 生式去除无用的A): A Þ ( A ) A Þ ( A ) ( A ) A Þ ( A ) ( A ) Þ ( A ) ( ) Þ (( A ) A ) ( ) Þ (( ) A ) ( ) Þ (( ) ( A ) A ) ( ) Þ (( ) ( A )) ( ) Þ (( ) (( A ) A )) ( ) Þ (( ) (( ) A )) ( ) Þ (( ) (( ))) ( ) 例3.6 例3 . 4中的语句文法用 -产生式还可写作: statement → if-stmt | o t h e r if-stmt → if ( e x p ) statement else-part e l s e - p a rt → else statement | exp → 0 | 1 请注意, -产生式指出结构else part是可选的。 例3.7 考虑一个语句序列的以下文法G: stmt-sequence → stmt ; s t m t - s e q u e n c e | s t m t stmt → s 这个文法生成由分号分隔开的一个或多个语句序列(语句已被提练到单个终结符 s中了): L(G) = { s, s;s, s;s;s, ...} 如要允许语句序列也可为空,则可写出以下的文法 G’: stmt-sequence → stmt ; stmt-sequence | stmt → s 但是它将分号变为一个语句结束符号(t e r m i n a t o r)而不是分隔符(s e p a r a t o r): L(G’) = { , s;, s;s;, s;s;s;, ...} 7 6 编译原理及实践 下载

China-pub.com 下载H 第3章上下文无关文法及分析 77 如果允许语句序列可为空,但仍要求保留分号作为语句分隔符,则须将文法写作: stmt-sequence nonempty-stmt-sequence nonempty-stmt-sequence-stmt:nonempty-stmt-sequence simt stt→s 这个例子说明在构造可选结构时,必须留意e-产生式的位置。 3.3分析树与抽象语法树 3.3.1分析树 推导为构造来自一个初始的非终结符的特定终结符的串提供了一个办法,但是推导并未唯 一地表示出它们所构造的结构。总而言之,对于同一个串可有多个推导。例如,使用图31中 的推导从简单表达式文法构造出记号串 n number) 图3-2给出了这个串的另一个推导。二者唯一的差别在于提供的替换顺序,而这其实是一 个很表面的差别。为了把它表示得更清楚一些,我们需要表示出终结符串的结构,而这些终结 符将推导的主要特征抽取出来,同时却将表面的差别按顺序分解开来。这样的表示法就是树结 构,它称作分析树。 (1)eD→exp op exp 【ep+exp op exp 2) →(ep)opep [ep→(ep)] 3 →(exp op exp)pep 【ep+exp op exp ber op exp) op exp ep→umber] exp)op exp [op→-】 (6 →number-number)pep [ep→number】 (7) →(number-number)texp [op-+】 (8) (number-number)*number 【ep→number] 图3-2表达式34-3)42的另一个推导 与推导相对应的分析树(parse tree)是一个作了标记的树,其中内部的节点由非终结符标 出,树叶节点由终结符标出,每个内部节点的子节点都表示推导的一个步骤中的相关非终结符 的替换。 以下是一个简单的示例,推导: ep exp op exp →number op exp →number+ep number+number 与分析树
如果允许语句序列可为空,但仍要求保留分号作为语句分隔符,则须将文法写作: stmt-sequence → nonempty-stmt-sequence | nonempty-stmt-sequence → stmt ; nonempty-stmt-sequence | s t m t stmt → s 这个例子说明在构造可选结构时,必须留意 - 产生式的位置。 3.3 分析树与抽象语法树 3.3.1 分析树 推导为构造来自一个初始的非终结符的特定终结符的串提供了一个办法,但是推导并未唯 一地表示出它们所构造的结构。总而言之,对于同一个串可有多个推导。例如,使用图 3 - 1中 的推导从简单表达式文法构造出记号串 ( number - number ) * n u m b e r 图3 - 2给出了这个串的另一个推导。二者唯一的差别在于提供的替换顺序,而这其实是一 个很表面的差别。为了把它表示得更清楚一些,我们需要表示出终结符串的结构,而这些终结 符将推导的主要特征抽取出来,同时却将表面的差别按顺序分解开来。这样的表示法就是树结 构,它称作分析树。 图3-2 表达式( 3 4 - 3 ) * 4 2 的另一个推导 与推导相对应的分析树(parse tree)是一个作了标记的树,其中内部的节点由非终结符标 出,树叶节点由终结符标出,每个内部节点的子节点都表示推导的一个步骤中的相关非终结符 的替换。 以下是一个简单的示例,推导: e x p Þ exp op exp Þ number op exp Þ number + e x p Þ number + n u m b e r 与分析树 第 3章 上下文无关文法及分析 7 7 下载
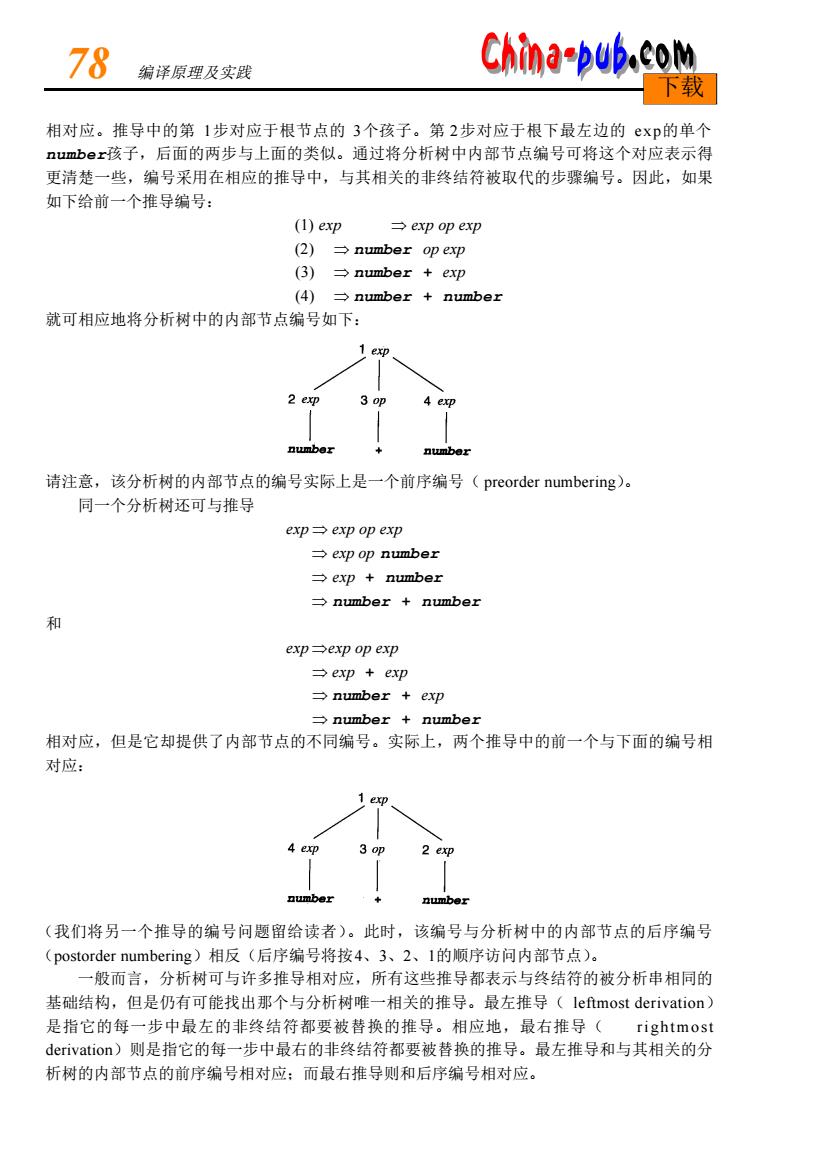
78 翁译原理及实践 China-pub.co 下载 相对应。推导中的第1步对应于根节点的3个孩子。第2步对应于根下最左边的exp的单个 umberi孩子,后面的两步与上面的类似。通过将分析树中内部节点编号可将这个对应表示得 更清楚一些,编号采用在相应的推导中,与其相关的非终结符被取代的步骤编号。因此,如果 如下给前一个推导编号: (1)exp →exp op exp (2)number op exp (3)→number+exp (4)→number+number 就可相应地将分析树中的内部节点编号如下: 请注意,该分析树的内部节点的编号实际上是一个前序编号(preorder numbering): 同一个分析树还可与推导 ep→exp op exp →exp op number →exp+number →number+number 布 expexp op exp →exp+exp number exp mber n mbe: 相对应,但是它却提供了内部节点的不同编号。实际上,两个推导中的前一个与下面的编号相 对应: (我们将另一个推导的编号问题留给读者)。此时,该编号与分析树中的内部节点的后序编号 (postorder numbering)相反(后序编号将按4、3、2、1的顺序访问内部节点)。 般而言,分析树可与许多推导相对应,所有这些推导都表示与终结符的被分析串相同的 基础结构,但是仍有可能找出那个与分析树唯一相关的推导。最左推导(leftmost derivation) 是指它的每一步中最左的非终结符都要被替换的推导。相应地,最右推导( rightmos derivation)则是指它的每一步中最右的非终结符都要被替换的推导。最左推导和与其相关的分 析树的内部节点的前序编号相对应:而最右推导则和后序编号相对应
相对应。推导中的第 1步对应于根节点的 3个孩子。第 2步对应于根下最左边的 e x p的单个 n u m b e r孩子,后面的两步与上面的类似。通过将分析树中内部节点编号可将这个对应表示得 更清楚一些,编号采用在相应的推导中,与其相关的非终结符被取代的步骤编号。因此,如果 如下给前一个推导编号: (1) e x p Þ exp op exp ( 2 ) Þ number op exp ( 3 ) Þ number + e x p ( 4 ) Þ number + n u m b e r 就可相应地将分析树中的内部节点编号如下: 请注意,该分析树的内部节点的编号实际上是一个前序编号( preorder numbering)。 同一个分析树还可与推导 e x p Þ exp op exp Þ exp op n u m b e r Þ e x p + number Þ number + n u m b e r 和 e x p Þexp op exp Þ e x p + e x p Þ number + e x p Þ number + n u m b e r 相对应,但是它却提供了内部节点的不同编号。实际上,两个推导中的前一个与下面的编号相 对应: (我们将另一个推导的编号问题留给读者)。此时,该编号与分析树中的内部节点的后序编号 (postorder numbering)相反(后序编号将按4、3、2、1的顺序访问内部节点)。 一般而言,分析树可与许多推导相对应,所有这些推导都表示与终结符的被分析串相同的 基础结构,但是仍有可能找出那个与分析树唯一相关的推导。最左推导( leftmost derivation) 是指它的每一步中最左的非终结符都要被替换的推导。相应地,最右推导( r i g h t m o s t d e r i v a t i o n)则是指它的每一步中最右的非终结符都要被替换的推导。最左推导和与其相关的分 析树的内部节点的前序编号相对应;而最右推导则和后序编号相对应。 7 8 编译原理及实践 下载