
China-pub.Co 下载 第5章 自底向上的分析 本章要点 ·自底向上分析概览 ·Yacc:LALR(I)分析程序的生成器 LR(O)项的有穷自动机及LRO)分析 ·使用Yacc生成TINY分析程序 ·SLR(1)分析 ·自底向上分析程序中的错误校正 ·一般的LR(I)和LALR(I)分析 前一章涉及到了递归下降和预测分析的自项向下分析的基本算法。在本章中,我们将描述 主要的自底向上的分析技术及其相关的构造。如在自顶向下的分析一样,我们将主要学习利用 最多 一个先行符号的分析算法,此外再谈一下如何扩展这个算法。 与LL(1)分析程序的术语相类似,最普通的自底向上算法称作LR(1)分析(LR(1) parsing)L表示由左向右处理输入,R表示生成了最右推导,而数字1则表示使用了先行的 个符号)。自底向上分析的作用还表现在它使得LR(O)分析(LR(O)parsing)也具有了意义,此 时在作出分析决定时没有考虑先行(因为可在先行记号出现在分析栈上之后再检查它,而且 倘若是这样发生的,它也就不会被算作先行了,所以这是可能的)SLR(I)分析(SLR( parsing,可简写为LR(I)分析)是对LR(1)分析的改进,它使用了一些先行。LALR(1)分析 (LALR(I)parsing,意即先行LR(I)分析)是比SLR(I)分析略微强大且比一般的LR(I)分析简 单的方法。 在本章节中将会谈到以上每一个分析方法的必要构造。这将包括LR(O)的DFA构造以及 LR(I)各项:SLR(I、LR(I)和LALR(I)分析算法的描述,以及相关分析表的构造。我们还将描 述Yacc(一个LALR(I)分析程序生成器)的用法,并为TINY语言使用Yacc生成一个分析程序,该 TNY语言构造出与在第5意中由递归下降分析程序开发的相同的语法树。 般而言,自底向上的分析算法的功能比自顶向下的方法强大(例如,左递归在自底向上 分析中就不成问题)。但是这些算法所涉及到的构造却更为复杂。因此,需要小心对它们的描 述,我们还需要利用文法的十分简单的示例来介绍它们。本章的开头先给出了这样的两个例 子,本章还会一直用到这两个例子。此外还会用到一些前章中的例子(整型算术表达式、语 句等等)。但是由于为全TNY语言用手工执行任何的自底向上的分析算法非常复杂,所以我 们并不打算完成它。实际上,所有重要的自底向上方法对于手工编码而言都太复杂了,但是 对于诸如Ycc的分析程序生成器却很合适。但是了解方法的操作却很重要,这样作为编译程 序的编写者就可对分析程序生成器的行为进行正确地分析了。由于分析程序生成器可以用 BNF中建议的语言语法来识别可能的问题,所以程序设计语言的设计者还可从这个信息中获 益不少。 为了掌握好自底向上的分析算法,读者还需要了解前面讲过的内容,这其中包括了有穷自 动机、从一个NFA中构造DFA的子集(第2章的2.3节和2.4节)、上下文无关文法的一般特性、推 导和分析树(第3章的3.2节和3.3节)。有时也需要用到FolIow集合(第4章的4.3节)。这一章从自底 向上的分析的概况开始谈起
下载 第5章 自底向上的分析 本章要点 • 自底向上分析概览 • Yacc: LALR(1)分析程序的生成器 • LR(0)项的有穷自动机及L R ( 0 )分析 • 使用Ya c c生成T I N Y分析程序 • SLR(1)分析 • 自底向上分析程序中的错误校正 • 一般的L R ( 1 )和L A L R ( 1 )分析 前一章涉及到了递归下降和预测分析的自顶向下分析的基本算法。在本章中,我们将描述 主要的自底向上的分析技术及其相关的构造。如在自顶向下的分析一样,我们将主要学习利用 最多一个先行符号的分析算法,此外再谈一下如何扩展这个算法。 与L L ( 1 )分析程序的术语相类似,最普通的自底向上算法称作 L R ( 1 )分析 ( L R ( 1 ) p a r s i n g ) ( L表示由左向右处理输入, R表示生成了最右推导,而数字 1则表示使用了先行的一 个符号 )。自底向上分析的作用还表现在它使得 L R ( 0 )分析(LR(0) parsing)也具有了意义,此 时在作出分析决定时没有考虑先行 (因为可在先行记号出现在分析栈上之后再检查它,而且 倘若是这样发生的,它也就不会被算作先行了,所以这是可能的 )。S L R ( 1 )分析 ( S L R ( 1 ) p a r s i n g,可简写为 L R ( 1 )分析)是对L R ( 1 )分析的改进,它使用了一些先行。 L A L R ( 1 )分析 (LALR(1) parsing,意即先行 L R ( 1 )分析)是比S L R ( 1 )分析略微强大且比一般的 L R ( 1 )分析简 单的方法。 在本章节中将会谈到以上每一个分析方法的必要构造。这将包括 L R ( 0 )的D FA构造以及 L R ( 1 )各项:S L R ( 1 )、L R ( 1 )和L A L R ( 1 )分析算法的描述,以及相关分析表的构造。我们还将描 述Ya c c (一个L A L R ( 1 )分析程序生成器)的用法,并为T I N Y语言使用Ya c c生成一个分析程序,该 T I N Y语言构造出与在第5章中由递归下降分析程序开发的相同的语法树。 一般而言,自底向上的分析算法的功能比自顶向下的方法强大 (例如,左递归在自底向上 分析中就不成问题 )。但是这些算法所涉及到的构造却更为复杂。因此,需要小心对它们的描 述,我们还需要利用文法的十分简单的示例来介绍它们。本章的开头先给出了这样的两个例 子,本章还会一直用到这两个例子。此外还会用到一些前章中的例子 (整型算术表达式、 i f语 句等等)。但是由于为全 T I N Y语言用手工执行任何的自底向上的分析算法非常复杂,所以我 们并不打算完成它。实际上,所有重要的自底向上方法对于手工编码而言都太复杂了,但是 对于诸如Ya c c的分析程序生成器却很合适。但是了解方法的操作却很重要,这样作为编译程 序的编写者就可对分析程序生成器的行为进行正确地分析了。由于分析程序生成器可以用 B N F中建议的语言语法来识别可能的问题,所以程序设计语言的设计者还可从这个信息中获 益不少。 为了掌握好自底向上的分析算法,读者还需要了解前面讲过的内容,这其中包括了有穷自 动机、从一个N FA中构造D FA的子集(第2章的2 . 3节和2 . 4节)、上下文无关文法的一般特性、推 导和分析树(第3章的3 . 2节和3 . 3节)。有时也需要用到F o l l o w集合(第4章的4 . 3节)。这一章从自底 向上的分析的概况开始谈起

China-pub.com 第5章自底向上的分析 151 下载 5.1自底向上分析概览 自底向上的分析程序使用了显式栈来完成分析,这与非递归的自顶向下的分析程序相类似 分析栈包括记号和非终结符,以及一些后面将讨论到的其他信息。自底向上的分析开始时栈是 空的,在成功分析的末尾还包括了开始符号。因此,可将自底向上的分析示意为: InputString StartSymbol accept 其中,分析栈在左边,输入位于正中间,而分析程序的动作则在右边(此时,“接受”是所指出 的唯一动作) 自底向上的分析程序有两种可能的动作(除“接受”之外): )将终结符从输入的开头移进到栈的顶部。 2)假设有BNF选择A→a,将栈顶部的串α归约为非终结符A。 因此自底向上的分析程序有时称作是移进-归约分析程序⊙。移进动作是由书写单词shi指 出的。归约动作则由书写reduce单词给出且指出在归约中所用的BNF选择⊙。自底向上的分析 程序的另一个特征是:出于后面要讲到的技术原因,总是将文法与一个新的开始符号一同扩充 (augmented)。这就意味着若S是开始符号,那么就将新的开始符号S增加到文法中,同时还添 加一个单元产生式到前面的开始符号中: SS 下面是两个示例,之后再讨论这两个例子所表现出的自底向上分析的一些特性。 例5.1考虑以下用于成对括号的扩充文法: S-S S·(S)lE 表51给出了使用该文法的串()的自底向上的分析。 表5-1例5.1中文法的自底向上分析程序的分析动作 分析栈 输入 动作 ()s 移进 2 s( 用S一归约 3 S (S )S 移进 4 S IS) 用S+e白约 s 用S一()S归约 6 55 s 用S一S阳约 7 SS 接受 是惯例却是添加rede
5.1 自底向上分析概览 自底向上的分析程序使用了显式栈来完成分析,这与非递归的自顶向下的分析程序相类似。 分析栈包括记号和非终结符,以及一些后面将讨论到的其他信息。自底向上的分析开始时栈是 空的,在成功分析的末尾还包括了开始符号。因此,可将自底向上的分析示意为: $ I n p u t S t r i n g $ . . . . . . . . . . . . $ S t a rt S y m b o l $ a c c e p t 其中,分析栈在左边,输入位于正中间,而分析程序的动作则在右边 (此时,“接受”是所指出 的唯一动作)。 自底向上的分析程序有两种可能的动作(除“接受”之外): 1) 将终结符从输入的开头移进到栈的顶部。 2) 假设有B N F选择A→a,将栈顶部的串a归约为非终结符A。 因此自底向上的分析程序有时称作是移进-归约分析程序 。移进动作是由书写单词s h i f t指 出的。归约动作则由书写 re d u c e单词给出且指出在归约中所用的 B N F选择 。自底向上的分析 程序的另一个特征是:出于后面要讲到的技术原因,总是将文法与一个新的开始符号一同扩充 ( a u g m e n t e d )。这就意味着若S是开始符号,那么就将新的开始符号 S¢ 增加到文法中,同时还添 加一个单元产生式到前面的开始符号中: S¢ → S 下面是两个示例,之后再讨论这两个例子所表现出的自底向上分析的一些特性。 例5.1 考虑以下用于成对括号的扩充文法: S¢ → S S → ( S ) S | 表5 - 1给出了使用该文法的串( )的自底向上的分析。 表5-1 例5 . 1中文法的自底向上分析程序的分析动作 分 析 栈 输 入 动 作 1 $ ( ) $ 移进 2 $ ( ) $ 用S→e 归约 3 $ (S ) $ 移进 4 $ ( S ) $ 用S→ 归约 5 $ (S) S $ 用S→ (S) S归约 6 $ S $ 用S¢→S归约 7 $ S¢ $ 接受 第 5章 自底向上的分析 1 5 1 下载 由于相同的原因,自顶向下的分析程序可被称作生成-匹配分析程序,但这并未成为惯例。 在归约的情况中,可如同在自顶向下分析中为一个生成动作所做的一样,仅仅由 B N F选择自身写出即可,但 是惯例却是添加re d u c e

152 翁译原理及实践 China-pub.Co 下载 例5.2考虑以下基本算术表达式的扩充文法(没有括号,只有一种运算): E'-E E→E+nln 表5-2是串n+n使用这个文法的自底向上的分析。 表5-2例5.2中文法的自底向上分析程序的分析动作 分析栈 输入 动作 $ n+nS 移进 2 +n 用E+n归的 3 SE 移进 SE+ ns 移选 SE+ 用E一E+a归约 6 SE 用E一E白约 7 SE 接受 在使用先行上,自底向上的分析程序比自项向下的分析程序的困难要小。实际上,自底向 上的分析程序可将输入符号移进到栈里直到它判断出要执行的是何种动作为止(假设判断一个 动作可以不要求将符号移进到输入中)。但是为了判断要完成的动作,自底向上的分析程序会 需要在栈内看得更深,而不仅仅是项部。例如,在表5-1中的第5行,S位于栈的项部,且分析 程序用产生式S一(S)S归约,而第6行在栈的顶部也有S,但是分析程序却用S一S归约。为了 能够了解S一(SS在第5步中是一个有效的归约,我们必须知道实际上栈在该点包含了串(S)S。 因此,自底向上的分析要求任意的“栈先行”。由于分析程序本身建立了钱且可使恰当的信息 成为可用的,所以这几乎同输入先行一样重要。此时所用的机制是“项”的确定性的有穷自动 机,下一节将会讲到它。 当然,仅仅了解栈的内容并不足以可唯一地判断出移进-归约分析的下一步,还需将输入 中的记号作为一个先行来考虑。例如在表5-2的第3行,E在栈中,且发生了一个移进:但在第6 行中,E又在栈中,但却用了E一E归约。两者的区别在于:在第3行中,输入的下一个记号是 “+”:但在第6行中,下一个输入记号却是$。因此, 任何执行那个分析的算法必须使用下一个 输入记号(先行)来判断出适当的动作。不同的移进-归约分析方法以不同的方式使用先行,而 这将导致具有不同能力和复杂性的分析程序。在看到单个算法之前,我们首先做一些普通的观 察来看看自底向上分析的直接步骤是如何表现特征的。 首先,我们再次注意到移进-归约分析程序描绘出输入串的最右推导,但推导步骤的顺序 却是颠倒的。在表5-1中,共有4个归约,它们与最右推导的4个步骤对应的顺序相反: S→S→(S→S(S)→() 在表5-2中,相对应的推导是 E'SE三E+n-n+n 我们将这样的推导中的终结符和非终结符的每个中间串都称作右句型(right sentential f「m)。在移讲-归约分析中,每个这样的白型都被分析线和输入分摄开。例如,发生在前面推 导中的第3步的右句子格式E+出现在表5-2的第3、第4和第5步。如果通过符号指出每一时 刻栈的顶部位于何处(即:当在栈和输入之间发生了分隔),则表5-2的第3步就由E‖+给出, 而其第4步则由E+‖给出。在每一种情况下,分析栈的符号序列都被称作右句型的可行前缀
例5.2 考虑以下基本算术表达式的扩充文法(没有括号,只有一种运算): E¢→ E E → E + n | n 表5 - 2是串n + n 使用这个文法的自底向上的分析。 表5-2 例5 . 2中文法的自底向上分析程序的分析动作 分 析 栈 输 入 动 作 1 $ n + n $ 移进 2 $ n + n $ 用E→n 归约 3 $ E + n $ 移进 4 $ E + n $ 移进 5 $ E + n $ 用E→E + n 归约 6 $ E $ 用E¢→ E归约 7 $ E¢ $ 接受 在使用先行上,自底向上的分析程序比自顶向下的分析程序的困难要小。实际上,自底向 上的分析程序可将输入符号移进到栈里直到它判断出要执行的是何种动作为止 (假设判断一个 动作可以不要求将符号移进到输入中 )。但是为了判断要完成的动作,自底向上的分析程序会 需要在栈内看得更深,而不仅仅是顶部。例如,在表 5 - 1中的第5行,S位于栈的顶部,且分析 程序用产生式S→ (S) S归约,而第6行在栈的顶部也有S,但是分析程序却用S¢→S归约。为了 能够了解S→(S) S在第5步中是一个有效的归约,我们必须知道实际上栈在该点包含了串(S) S。 因此,自底向上的分析要求任意的“栈先行”。由于分析程序本身建立了栈且可使恰当的信息 成为可用的,所以这几乎同输入先行一样重要。此时所用的机制是“项”的确定性的有穷自动 机,下一节将会讲到它。 当然,仅仅了解栈的内容并不足以可唯一地判断出移进-归约分析的下一步,还需将输入 中的记号作为一个先行来考虑。例如在表 5 - 2的第3行,E在栈中,且发生了一个移进;但在第6 行中,E又在栈中,但却用了E¢→E 归约。两者的区别在于:在第3行中,输入的下一个记号是 “+”;但在第6行中,下一个输入记号却是$。因此,任何执行那个分析的算法必须使用下一个 输入记号(先行)来判断出适当的动作。不同的移进-归约分析方法以不同的方式使用先行,而 这将导致具有不同能力和复杂性的分析程序。在看到单个算法之前,我们首先做一些普通的观 察来看看自底向上分析的直接步骤是如何表现特征的。 首先,我们再次注意到移进-归约分析程序描绘出输入串的最右推导,但推导步骤的顺序 却是颠倒的。在表5 - 1中,共有4个归约,它们与最右推导的4个步骤对应的顺序相反: S¢ Þ S Þ (S) Þ S (S) Þ ( ) 在表5 - 2中,相对应的推导是 E¢ Þ E Þ E + n Þ n + n 我们将这样的推导中的终结符和非终结符的每个中间串都称作右句型 (right sentential f o r m )。在移进-归约分析中,每个这样的句型都被分析栈和输入分隔开。例如,发生在前面推 导中的第3步的右句子格式E + n 出现在表5 - 2的第3、第4和第5步。如果通过符号 || 指出每一时 刻栈的顶部位于何处(即:当在栈和输入之间发生了分隔 ),则表5 - 2的第3步就由E || + n给出, 而其第4步则由E + || n给出。在每一种情况下,分析栈的符号序列都被称作右句型的可行前缀 1 5 2 编译原理及实践 下载

China-pub.com 第5章自底向上的分析 153 下载 (viable prefix)。因此,E、E+和E+n都是右句型E+n的可行前缀,但右句子格式n+n却使 E和n作为它的可行前缓(表5-2的第1步和第2步)。请注意,n+不是n+n的可行前级。 移讲一归约分析程序将终结符从输入移讲到我直到它能执行一个归约以得到下一个右句子 格式。它发生在位于栈顶部的符号串匹配用于下一个归约的产生式的右边。这个串、它在右句 子格式中发生的位置以及用来归约它的产生式被称作右句型的句柄(handle)°。例如,在右句子 格式n+n中,它的句柄是由最左边的单个记号n与用来归约它以产生新的右句型E+n的产生 式E一n组成的串。这个新句型的句柄是整个串E+n(一个可行的前缀)以及产生式E一E+n。 有时由于表示法上的弊端,我们要用串本身来作为句柄。 判断分析中的下一个句柄是移进-归约分析程序的主要任务。请注意,句柄串总是为它的 产生式(在下一步的归约中使用的产生式)构成一个完整的右部,而且当归约发生时,句柄串的 最右边的位置将与栈的顶部相对应。所以对于移进-归约分析程序将要基于产生式右边的位置 来判断它的动作这一点而言,就看起来有些似是而非了。当这些位置到达产生式的右边末端时, 这个产生式就有可能是一个归约,而且句柄还有可能位于栈的顶部。但为了成为句柄,串位于 栈的顶部来匹配产生式的右边并不够。实际上,若£产生式可用于归约的话(如在例5.1中), 那么它的右边(空串)总是位于栈的顶部。归约仅发生在结果串实际为一个右句型时。例如,在 表51的第3步中,可完成用S一e归约,但是得到的串(SS并不是右句子格式,所以e在句子 格式(中的这个位置也不是句柄。 5.2LR(O)项的有穷自动机与LR(O)分析 5.2.1LR(0)项 上下文无关文法的LR(O)项(LR(O)item)(或简写为项(item)是在其右边带有区分位置的产 生式选择。我们可用一个句点(当然它就变成了元符号,而不会与真正的记号相混淆)来指出 这个区分的位置。所以若A一α是产生式选择,且若B和y是符号的任何两个串(包括空串e) 且存在若y=a,那么A一BY就是LR(O)项。之所以称作LR(O)项是由于它们不包括先行的显 式引用。 例5.3考虑例5.1的文法: + 这个文法存在着3个产生式选择和8个项目: SS S→.(S)S S→(.S)S S-(S.)S S-(S).S S-(S)5 日如果文法有二义性。那么由此就会存在多于一个的推导,则在右句型中就会有多于一个的句柄。如果文法没 有二义性,则句柄就是唯一的
(viable prefix)。因此,E、E+ 和E + n 都是右句型E + n 的可行前缀,但右句子格式n + n 却使 和n 作为它的可行前缀(表5 - 2的第1步和第2步)。请注意,n + 不是n + n 的可行前缀。 移进-归约分析程序将终结符从输入移进到栈直到它能执行一个归约以得到下一个右句子 格式。它发生在位于栈顶部的符号串匹配用于下一个归约的产生式的右边。这个串、它在右句 子格式中发生的位置以及用来归约它的产生式被称作右句型的句柄 (handle) 。例如,在右句子 格式n + n 中,它的句柄是由最左边的单个记号n 与用来归约它以产生新的右句型E + n的产生 式E→n 组成的串。这个新句型的句柄是整个串 E + n (一个可行的前缀)以及产生式E→E + n。 有时由于表示法上的弊端,我们要用串本身来作为句柄。 判断分析中的下一个句柄是移进-归约分析程序的主要任务。请注意,句柄串总是为它的 产生式(在下一步的归约中使用的产生式 )构成一个完整的右部,而且当归约发生时,句柄串的 最右边的位置将与栈的顶部相对应。所以对于移进-归约分析程序将要基于产生式右边的位置 来判断它的动作这一点而言,就看起来有些似是而非了。当这些位置到达产生式的右边末端时, 这个产生式就有可能是一个归约,而且句柄还有可能位于栈的顶部。但为了成为句柄,串位于 栈的顶部来匹配产生式的右边并不够。实际上,若 产生式可用于归约的话(如在例 5 . 1中), 那么它的右边(空串)总是位于栈的顶部。归约仅发生在结果串实际为一个右句型时。例如,在 表5 - 1的第3步中,可完成用S→ 归约,但是得到的串(S S)并不是右句子格式,所以 在句子 格式(S)中的这个位置也不是句柄。 5.2 LR(0)项的有穷自动机与L R ( 0 )分析 5.2.1 LR(0)项 上下文无关文法的L R ( 0 )项(LR(0) item)(或简写为项( i t e m ) )是在其右边带有区分位置的产 生式选择。我们可用一个句点 (当然它就变成了元符号,而不会与真正的记号相混淆 )来指出 这个区分的位置。所以若 A→a是产生式选择,且若 b和g 是符号的任何两个串(包括空串 ), 且存在着bg =a,那么A→b.g 就是L R ( 0 )项。之所以称作 L R ( 0 )项是由于它们不包括先行的显 式引用。 例5.3 考虑例5 . 1的文法: S¢→S S→( S ) S | 这个文法存在着3个产生式选择和8个项目: S¢→.S S¢→S. S→. ( S ) S S→( .S ) S S→( S. )S S→( S ) .S S→( S )S. 第 5章 自底向上的分析 1 5 3 下载 如果文法有二义性,那么由此就会存在多于一个的推导,则在右句型中就会有多于一个的句柄。如果文法没 有二义性,则句柄就是唯一的

154翁译原理及实我 China-pub.co 下载 S 例5.4例5.2的文法存在着以下的8个项目: E→.E E→E. E-.E+n E→E.+n E-E+.n E-E+n. E-.n E-n. 项目概念的思想就是指项目记录了特定文法规则右边识别中的中间步骤。特别地,项目A 一B.y是由文法规则选择A一构成(其中α=y),这一点意味着早已看到了B,且可能从 一个 输入记号中获取Y。从分析栈的观点来看,这就意味着B必须出现在栈的顶部。项目A一.α意味 着将要利用文法规则选择A一a识别4(将这样的项目称作初始项(initiate)。项目A→a.意味着 α现在位于分析栈的顶部,而且若A一α在下一个归约中使用的话,它有可能就是句柄(将这样 的项目称作完整项(complete item)。 5.2.2项目的有穷自动机 LR(O)项可作为一个保持有关分析栈和移进-归约分析过程的信息的有穷自动机的状态来 使用。这将从作为非确定性的有穷自动机开始。从这个LR(O)项的NFA中可利用第2章的子集构 造来构建出LR(O)项集合的DFA。正如将要看到的一样,直接构造LR(O)项集合的DFA也是很简 单的。 LR(O)项的NFA的转换是什么呢?若有项目A一aY,且假设y以符号开始,其中X可以是 记号或非终结符,所以该项目就可写作A→αX.。那么在符号X上就有一个从由该项目代表的 状态到由项目A一αXn代表的状态的转换。把它写在一般格式中,就是: 若X是一个记号,那么该转换与X的一个在分析中从输入到栈顶部的移进相对应。另一方面, (A一a可X一(A一a可 若X是一个非终结符,因为X永远不会作为输入符号出现,所以该转换的解释就复杂了。实际 上,这样的转换仍与在分析时将X压入到栈中相对应,但是它只发生在由产生式X一β形成的归 约时。由于这样的归约前面必须有一个B的识别,而且由初始项X一阝给出的状态代表了这个处 理的开始(句点指出将要识别一个B),则对于每个项目A→αX,必须为X的每个产生式X一B添 加一个e产生式, 它指示通过识别它的产生式的右边的任意匹配来产生X。 这两种情况只表示LR(O)项的NFA中的转换,它并未讨论到NFA的初始状态和接受状态
S→. 例5.4 例5 . 2的文法存在着以下的8个项目: E¢→.E E¢→E. E→.E + n E→E. + n E→E + .n E→E + n. E→.n E→n. 项目概念的思想就是指项目记录了特定文法规则右边识别中的中间步骤。特别地,项目 A →b.g 是由文法规则选择A→a构成(其中a = b g),这一点意味着早已看到了b,且可能从下一个 输入记号中获取g。从分析栈的观点来看,这就意味着 b必须出现在栈的顶部。项目 A→.a意味 着将要利用文法规则选择A→a识别A(将这样的项目称作初始项(initial item)。项目A→a.意味着 a现在位于分析栈的顶部,而且若 A→a在下一个归约中使用的话,它有可能就是句柄(将这样 的项目称作完整项(complete item))。 5.2.2 项目的有穷自动机 L R ( 0 )项可作为一个保持有关分析栈和移进-归约分析过程的信息的有穷自动机的状态来 使用。这将从作为非确定性的有穷自动机开始。从这个 L R ( 0 )项的N FA中可利用第2章的子集构 造来构建出L R ( 0 )项集合的D FA。正如将要看到的一样,直接构造 L R ( 0 )项集合的D FA也是很简 单的。 L R ( 0 )项的N FA的转换是什么呢?若有项目 A→a.g,且假设g 以符号X开始,其中X可以是 记号或非终结符,所以该项目就可写作 A→aX.h。那么在符号X上就有一个从由该项目代表的 状态到由项目A→aX.h代表的状态的转换。把它写在一般格式中,就是: 若X是一个记号,那么该转换与 X的一个在分析中从输入到栈顶部的移进相对应。另一方面, 若X是一个非终结符,因为 X永远不会作为输入符号出现,所以该转换的解释就复杂了。实际 上,这样的转换仍与在分析时将 X压入到栈中相对应,但是它只发生在由产生式 X→b形成的归 约时。由于这样的归约前面必须有一个 b的识别,而且由初始项X→.b给出的状态代表了这个处 理的开始(句点指出将要识别一个b),则对于每个项目A→a.Xh,必须为X的每个产生式X→b添 加一个 产生式, 它指示通过识别它的产生式的右边的任意匹配来产生 X。 这两种情况只表示 L R ( 0 )项的N FA中的转换,它并未讨论到 N FA的初始状态和接受状态。 1 5 4 编译原理及实践 下载

China-pub.com 第5章自底向上的分析 155 下载 NFA的初始状态应与分析程序的初始状态相对应:栈是空的,而且将要识别一个S,其中S是 文法的开始符号。因此,任何由S的产生式选择构造的初始项S一α都可作为开始状态。不幸的 是,S可能有许多这样的产生式,如何知道该选择哪一个呢?实际上,我们是无法做到这一点 的。其解决办法是通过产生式S→S扩充(augment)文法,其中S是一个新的非终结符。接着, S成为扩充文法(augmented grammar)的开始状态,且初始项S.S也成为NFA的开始状态。这 就是为什么扩充前面例子文法的原因。 在这个NFA中,哪些状态将成为接受状态呢?读者此时必须记住NFA的任务是用于了解 分析的状态,而不是如第2章中自动机那样被设计为完全识别串。因此,分析程序本身将决定 何时接受,而NFA则无需包含这一信息,所以NFA实际上根本就没有接受状态(NFA存在着有 关接受的一些信息,但并不是在接受状态中。在描述使用自动机制分析算法时还会讨论到这 一占)。 这样一来,LR(O)项的NFA的描述就完整了。现在来讨论前面两个例子的简单文法以及构 造它们的LR(O)项的NFA。 例5.55.3列出了例5.1的文法的8个LR(0)项,所以这个NFA就有8个状态,如图5-1所示。请注 意,图中在非终结符S之前带有一个句点的每个项目都有一个到S的每个初始项的ε-转换。 →5 (S)S. →(S).S 图-1例5.5中文法的LR(O)项的NFA 例5.6在例5.4中,我们列出了与例5.2中的文法相关的LR(0)项。图5-2是这些项目的NFA。请 注意,初始项E一E+·有一个到它自身的e转换(这种情况会出现在带有直接左递归的所有 文法中)。 为了完成项目用于了解分析状态的描述,我们必须根据第2章的子集构造来构建与项目的 NFA相对应的项目集合的DFA,这样之后就可说明LR(O)分析算法了。我们将执行前面刚给出 的NFA的两个例子的子集构造。 例5.7考虑图5-1的NFA。相关的DFA的开始状态是由项目S一S组成的集合的e-闭包,而这又 是3个项目的集合{S一S,S一.(S)S,S一.}由于S有一个从S一S到S一S的转换,所以也 就存在着一个从开始状态到DFA状态{S一S.}的对应转换(不存在从S一S到任何其他项目的E
N FA的初始状态应与分析程序的初始状态相对应:栈是空的,而且将要识别一个 S,其中S 是 文法的开始符号。因此,任何由 S的产生式选择构造的初始项S→.a都可作为开始状态。不幸的 是,S可能有许多这样的产生式,如何知道该选择哪一个呢?实际上,我们是无法做到这一点 的。其解决办法是通过产生式 S¢→S 扩充( a u g m e n t )文法,其中S¢是一个新的非终结符。接着, S¢ 成为扩充文法(augmented grammar)的开始状态,且初始项S¢→.S 也成为N FA的开始状态。这 就是为什么扩充前面例子文法的原因。 在这个N FA中,哪些状态将成为接受状态呢?读者此时必须记住 N FA的任务是用于了解 分析的状态,而不是如第 2章中自动机那样被设计为完全识别串。因此,分析程序本身将决定 何时接受,而N FA则无需包含这一信息,所以 N FA实际上根本就没有接受状态 ( N FA存在着有 关接受的一些信息,但并不是在接受状态中。在描述使用自动机制分析算法时还会讨论到这 一点)。 这样一来,L R ( 0 )项的N FA的描述就完整了。现在来讨论前面两个例子的简单文法以及构 造它们的L R ( 0 )项的N FA。 例5.5 5 . 3列出了例5 . 1的文法的8个L R ( 0 )项,所以这个N FA就有8个状态,如图5 - 1所示。请注 意,图中在非终结符S之前带有一个句点的每个项目都有一个到S的每个初始项的 - 转换。 图5-1 例5 . 5中文法的L R ( 0 )项的N FA 例5.6 在例5 . 4中,我们列出了与例5 . 2中的文法相关的L R ( 0 )项。图5 - 2是这些项目的N FA。请 注意,初始项E→.E + n 有一个到它自身的 - 转换(这种情况会出现在带有直接左递归的所有 文法中)。 为了完成项目用于了解分析状态的描述,我们必须根据第 2章的子集构造来构建与项目的 N FA相对应的项目集合的 D FA,这样之后就可说明 L R ( 0 )分析算法了。我们将执行前面刚给出 的N FA的两个例子的子集构造。 例5.7 考虑图5 - 1的N FA。相关的D FA的开始状态是由项目S¢→.S组成的集合的 -闭包,而这又 是3个项目的集合{ S¢→.S, S→. ( S ) S, S →. }。由于S有一个从S¢→ .S到S¢→ S.的转换,所以也 就存在着一个从开始状态到D FA状态{ S¢→ S. }的对应转换(不存在从S¢→ S.到任何其他项目的 第 5章 自底向上的分析 1 5 5 下载

156 翁译原理及实践 China-pub.Com 下载 转换)。在(上也有一个从开始状态到DFA状态的转换{S一(.S)SS.(S)S,S一.({S一( S)S;的e闭包)。DFA状态{S一(S)SS一.(S)S,S一.)在(上有到其自身的转换,在S上 也有到{S一(S)S}的转换。这个状态在(上有到状态{S(S).S,S.(S)S,S一.}的 转换。最后,这一最终状态在(上有到前面所构造的状态{S一(.S)S,S→.(S)S,S一.}的 转换。图5-3是完整的DFA,为了便于引用还给各个状态编了号(按照惯例,状态0是开始状态) E→.E E→E, E 图5-2例5.6中文法的LR(O)项的NFA ① ② S. 4 图5-3与图5的NFA相对应的项目集合的DFA 例5.8考虑图5-2的NFA。相关DFA的开始状态由3个项目的集合{E一E,E一.E+nE一n 组成。在E上有一个从项目E"一E到项目E'一E的转换,但在E上还有一个从项目E一E+n到 项目E一E.+n的转换。因此,在E上就有一个从DFA的开始状态到集合{E一E,E一E.+n} 的闭包的转换。由于没有任何一个来自这些项目的转换,所以这个集合就是它自身的闭包, 且构成了一个完整的DFA状态。来自开始状态还有另一个转换,它与符号n上的从E一.n到E →n.的转换相对应。因为没有来自项目E一n的e转换,所以这个项目是它自身的e闭包,且 构成了 个完整的DFA状态{E一n.}。由于没有来自这个状态的转换,所以被计算的唯一转 换仍来自于集合{E'一E,E一E.+n}。从该集合开始只有一个转换,它与符号+上的从项目E 一E.+n到项目E一E+,n的转换相对应。项目E一E+.n也没有e转换,所以就在DFA中构造 了一个单独的集合。最后,n上有一个从集合{E一E+.n)到集合{E→E+n}的转换。图5-4
转换)。在(上也有一个从开始状态到D FA状态的转换{ S→ (. S ) S, S→.( S ) S, S→. }({ S→ (. S ) S }的 闭包)。D FA状态{ S→ (. S ) S, S→ . ( S ) S, S→ . }在(上有到其自身的转换,在S上 也有到{ S→ ( S.) S }的转换。这个状态在(上有到状态{ S→ ( S ). S,S→ .( S ) S, S → . }的 转换。最后,这一最终状态在(上有到前面所构造的状态{ S→ (. S ) S, S→ .( S ) S, S → . }的 转换。图5 - 3是完整的D FA,为了便于引用还给各个状态编了号(按照惯例,状态0是开始状态)。 图5-2 例5 . 6中文法的L R ( 0 )项的N FA 图5-3 与图5 - 1的N FA相对应的项目集合的D FA 例5.8 考虑图5 - 2的N FA。相关D FA的开始状态由3个项目的集合{E¢→.E, E→.E + n, E →.n} 组成。在E上有一个从项目E¢→.E到项目E¢→ E.的转换,但在E上还有一个从项目E→.E + n 到 项目E→E. + n的转换。因此,在E上就有一个从D FA的开始状态到集合{ E¢→ E., E→E. + n} 的闭包的转换。由于没有任何一个来自这些项目的 转换,所以这个集合就是它自身的 闭包, 且构成了一个完整的 D FA状态。来自开始状态还有另一个转换,它与符号 n 上的从E→.n到E → n.的转换相对应。因为没有来自项目 E→n.的 转换,所以这个项目是它自身的 闭包,且 构成了一个完整的D FA状态{ E→ n. }。由于没有来自这个状态的转换,所以被计算的唯一转 换仍来自于集合{E¢→ E., E→E. + n}。从该集合开始只有一个转换,它与符号 +上的从项目E →E. + n 到项目E→E +.n 的转换相对应。项目E→E +.n 也没有 转换,所以就在D FA中构造 了一个单独的集合。最后, n 上有一个从集合{ E→E +.n}到集合{ E →E + n. }的转换。图5 - 4 1 5 6 编译原理及实践 下载
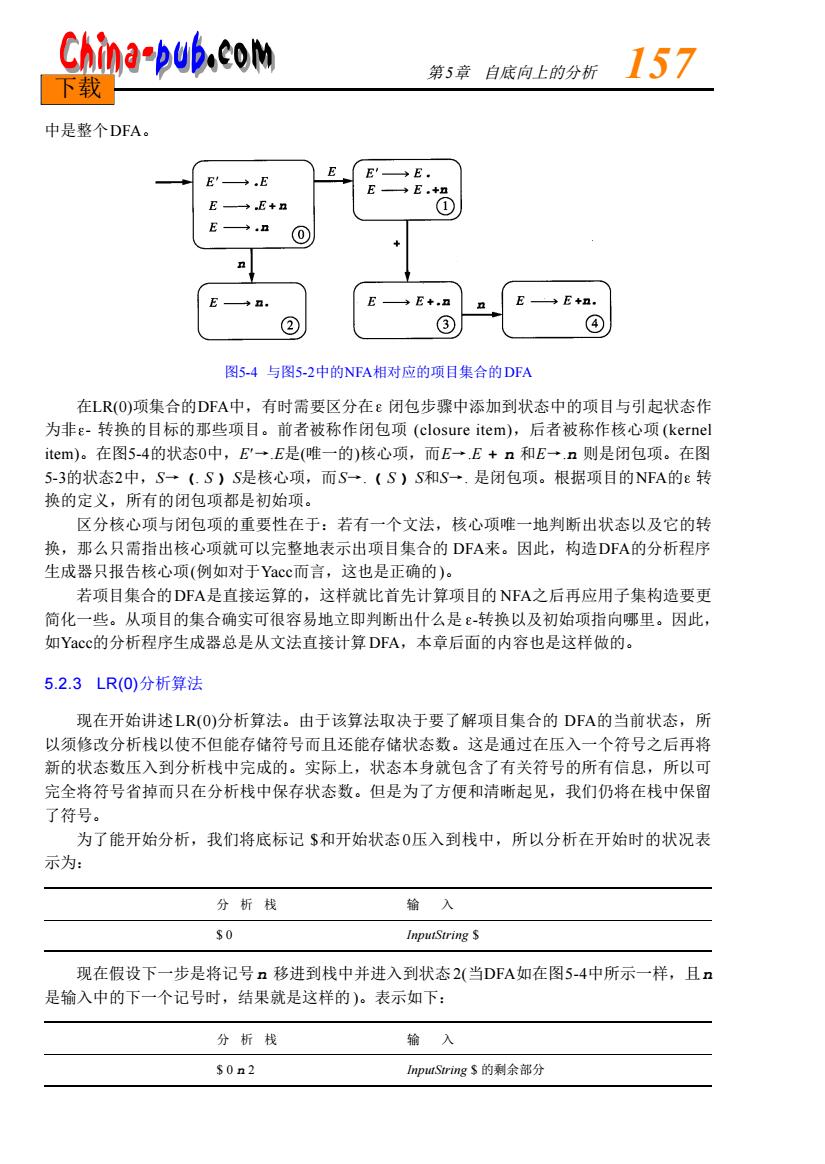
China-pub.com 第5章自底向上的分析 157 下载 中是整个DFA .E E E'→E (0 4E+,a ③ ④ 图5-4与图5-2中的NFA相对应的项目集合的DFA 在LR(O)项集合的DFA中,有时需要区分在E闭包步骤中添加到状态中的项目与引起状态作 为非e-转换的目标的那些项目。前者被称作闭包项(closure item),后者被称作核心项(kernel item)。在图5-4的状态0中,E'一E是(唯一的)核心项,而E一E+n和E,n则是闭包项。在图 53的状态2中,S一(.S)S是核心项,而S一.(S)S和S一.是闭包项。根据项目的NFA的E转 换的定义,所有的闭包项都是初始项。 区分核心项与闭包项的重要性在于:若有一个文法,核心项唯一地判断出状态以及它的转 换,那么只需指出核心项就可以完整地表示出项目集合的DFA来。因此,构造DFA的分析程序 生成器只报告核心项(例如对于Yacc而言,这也是正确的)。 若项目集合的DFA是直接运算的,这样就比首先计算项目的NFA之后再应用子集构造要更 简化一些。从项目的集合确实可很容易地立即判断出什么是-转换以及初始项指向哪里。因此, 如Yacc的分析程序生成器总是从文法直接计算DFA,本章后面的内容也是这样做的。 5.2.3LR(0)分析算法 现在开始讲述LR(O)分析算法。由于该算法取决于要了解项目集合的DFA的当前状态,所 以须修改分析栈以使不但能存储符号而且还能存储状态数。这是通过在压入一个符号之后再将 新的状态数压入到分析栈中完成的。实际上,状态本身就包含了有关符号的所有信息,所以可 完全将符号省掉而只在分析栈中保存状态数。但是为了方便和清晰起见,我们仍将在栈中保留 了符号。 为了能开始分析,我们将底标记$和开始状态0压入到栈中,所以分析在开始时的状况表 示为 分析栈 输入 InputString S 现在假设下一步是将记号n移进到栈中并进入到状态2(当DFA如在图5-4中所示一样,且n 是输入中的下一个记号时,结果就是这样的)。表示如下: 分析栈 输入 的剩余部分
中是整个D FA。 图5-4 与图5 - 2中的N FA相对应的项目集合的D FA 在L R ( 0 )项集合的D FA中,有时需要区分在 闭包步骤中添加到状态中的项目与引起状态作 为非 - 转换的目标的那些项目。前者被称作闭包项 (closure item),后者被称作核心项 ( k e r n e l i t e m )。在图5 - 4的状态0中,E¢→.E是(唯一的)核心项,而E→.E + n 和E→.n 则是闭包项。在图 5 - 3的状态2中,S→ (. S ) S是核心项,而S→. ( S ) S和S→. 是闭包项。根据项目的N FA的 转 换的定义,所有的闭包项都是初始项。 区分核心项与闭包项的重要性在于:若有一个文法,核心项唯一地判断出状态以及它的转 换,那么只需指出核心项就可以完整地表示出项目集合的 D FA来。因此,构造D FA的分析程序 生成器只报告核心项(例如对于Ya c c而言,这也是正确的)。 若项目集合的D FA是直接运算的,这样就比首先计算项目的 N FA之后再应用子集构造要更 简化一些。从项目的集合确实可很容易地立即判断出什么是 -转换以及初始项指向哪里。因此, 如Ya c c的分析程序生成器总是从文法直接计算D FA,本章后面的内容也是这样做的。 5.2.3 LR(0)分析算法 现在开始讲述L R ( 0 )分析算法。由于该算法取决于要了解项目集合的 D FA的当前状态,所 以须修改分析栈以使不但能存储符号而且还能存储状态数。这是通过在压入一个符号之后再将 新的状态数压入到分析栈中完成的。实际上,状态本身就包含了有关符号的所有信息,所以可 完全将符号省掉而只在分析栈中保存状态数。但是为了方便和清晰起见,我们仍将在栈中保留 了符号。 为了能开始分析,我们将底标记 $和开始状态0压入到栈中,所以分析在开始时的状况表 示为: 分 析 栈 输 入 $ 0 InputString $ 现在假设下一步是将记号n 移进到栈中并进入到状态2 (当D FA如在图5 - 4中所示一样,且n 是输入中的下一个记号时,结果就是这样的 )。表示如下: 分 析 栈 输 入 $ 0 n 2 InputString $ 的剩余部分 第 5章 自底向上的分析 1 5 7 下载

158 翁译原理及实践 China-pub.co 下载 LR(O)分析算法根据当前的DFA状态选择一个动作,这个状态总是出现在栈的顶部。 定义:LR(O)分析算法(LR(O)parsing algorithm)。令s为当前的状态(位于分析栈的顶 部)。则动作定义如下: 1.若状态s包含了格式A→α邓的任何项目,其中X是一个终结符,则动作就是将 当前的输入记号移进到栈中。若这个记号是X,且状态s包含了项目A一→αX郑, 则压入到栈中的新状态就是包含了项目A→αXB的状态。若由于位于刚才所描 述的格式的状态s中的某个项目,这个记号不是X,则声明一个错误。 2.若状态s包含了任何完整的项目(格式A→a.的一个项目),则动作是用规则A→α 归约。假设输入为空,用规则S一S归约(其中S是开始状态)与接受相等价:若输 入不为空,则出现错误。在所有的其他情况中,新状态的计算如下:将串α及它 的所有对应状态从分析栈中删去(根据DFA的构造方式,串α必须位于栈的顶部)。 相应地,在DFA中返回到由a开始构造的状态中(这须是由α的刷除所揭示的状 态)。由于构造DFA,这个状态就还须包含格式B一QAB的一个项目。将A压入到 栈中,并压入包含了项目B一AB的状态(作为新状态)。(请注意,由于正将 压入到栈中,所以这与在DFA中跟随A的转换相对应(这实际上是合理的)。 若以上的规则都是无歧义的,则文法就是LR(O)文法(LR(O)grammar)。这就意味着若 状态包含了完整项目A→α.,那么它就不能再包含其他项目了。实际上,若这样的状态还包含 了一个“移进的”项目A→α郑(X是一个终结符),就会出现一个到底是执行动作(1)还是执 行动作(2)的二义性。这种情况称作移进-归约冲突(shift-reduce confliet)。类似地,如果这样 的状态包含了另一个完整项目B一B.,那么也会出现一个关于为该归约使用哪个产生式(4→α 或B一B)二义性。这种情况称作归约-归约冲突(reduce-reduce conflict))。所以,当仅当每个 状态都是移进状态(仅包含了“移进”项目的状态)或包含了单个完整项目的归约时,该文法才 是LR(O). 我们注意到上面例子中所用到的两个文法都不是LR(O)文法。在图5-3中,状态0、状态2和 状态4都包括了对于LR(O)分析算法的移进-归约冲突:在图5-4的DFA中,状态1包含了一个移 进-归约冲突。由于几乎所有“真正的”文法都不是LR(O),所以这并不奇怪。但下面将会给出 一个文法是LR(O)的示例。 例5.9考虑文法 A-(A)川a 扩充的文法具有如图5-5所示的项目集合的DFA,而这就是LR(O)。为了看清LR(O)分析算法 是如何工作的,可考虑一下串(a)。该串的分析是根据表5-3各步骤所给出的LR(O)分析算 法进行。分析开始于状态0,因为这个状态是一个移进状态,所以将第1个记号(移进到栈中。 接着,由于DFA指出了在符号(上从状态0到状态3的转换,所以将状态3压入到栈中。状态3 也是一个移进状态,所以下一个(也被移进到栈中,而且在(上的转换返回到状态3。移进再 一次将a放入到栈中,而且a上的转换由状态3进入到状态2。现在位于表5-3的第4步,而且 己到达了第1个归约状态。这里的状态2和符号a都是由栈弹出的,并回到处理中的状态3。接 着,将A压入到栈中,且得到由状态3到状态4的4转换。状态4是一个移进状态,所以)被移 进到栈中,且)上的转换使分析转到状态5。这里发生了一个由规则A一(A)进行的归约 它从栈中弹出状态5、状态4、状态3以及符号)、A和)。现在的分析位于状态3中,而且A和
L R ( 0 )分析算法根据当前的D FA状态选择一个动作,这个状态总是出现在栈的顶部。 定义:L R ( 0 )分析算法(LR(0) parsing algorithm)。令s 为当前的状态(位于分析栈的顶 部)。则动作定义如下: 1. 若状态s 包含了格式A→a.Xb的任何项目,其中X是一个终结符,则动作就是将 当前的输入记号移进到栈中。若这个记号是 X,且状态s 包含了项目A→a.Xb, 则压入到栈中的新状态就是包含了项目 A→aX.b的状态。若由于位于刚才所描 述的格式的状态s 中的某个项目,这个记号不是X,则声明一个错误。 2. 若状态s 包含了任何完整的项目(格式A→a. 的一个项目),则动作是用规则A→a 归约。假设输入为空,用规则S¢→S归约(其中S是开始状态)与接受相等价;若输 入不为空,则出现错误。在所有的其他情况中,新状态的计算如下:将串a及它 的所有对应状态从分析栈中删去(根据DFA的构造方式,串a必须位于栈的顶部)。 相应地,在D FA中返回到由a开始构造的状态中(这须是由a的删除所揭示的状 态)。由于构造D FA,这个状态就还须包含格式B→a.Ab的一个项目。将A压入到 栈中,并压入包含了项目B→aA.b的状态(作为新状态)。(请注意,由于正将A 压入到栈中,所以这与在DFA中跟随A的转换相对应(这实际上是合理的)。 若以上的规则都是无歧义的,则文法就是 L R ( 0 )文法(LR(0) grammar)。这就意味着若一个 状态包含了完整项目A→a.,那么它就不能再包含其他项目了。实际上,若这样的状态还包含 了一个“移进的”项目 A→a.Xb(X是一个终结符 ),就会出现一个到底是执行动作 ( 1 )还是执 行动作( 2 )的二义性。这种情况称作移进-归约冲突 (shift-reduce conflict)。类似地,如果这样 的状态包含了另一个完整项目 B→b.,那么也会出现一个关于为该归约使用哪个产生式 (A→a 或B→b)二义性。这种情况称作归约-归约冲突 (reduce-reduce conflict)。所以,当仅当每个 状态都是移进状态(仅包含了“移进”项目的状态 )或包含了单个完整项目的归约时,该文法才 是L R ( 0 )。 我们注意到上面例子中所用到的两个文法都不是 L R ( 0 )文法。在图5 - 3中,状态0、状态2和 状态4都包括了对于L R ( 0 )分析算法的移进-归约冲突;在图 5 - 4的D FA中,状态1包含了一个移 进-归约冲突。由于几乎所有“真正的”文法都不是 L R ( 0 ),所以这并不奇怪。但下面将会给出 一个文法是L R ( 0 )的示例。 例5.9 考虑文法 A→ ( A ) | a 扩充的文法具有如图 5 - 5所示的项目集合的 D FA,而这就是 L R ( 0 )。为了看清 L R ( 0 )分析算法 是如何工作的,可考虑一下串 ( ( a ) )。该串的分析是根据表 5 - 3各步骤所给出的 L R ( 0 )分析算 法进行。分析开始于状态 0,因为这个状态是一个移进状态,所以将第 1个记号(移进到栈中。 接着,由于 D FA指出了在符号 (上从状态0到状态3的转换,所以将状态 3压入到栈中。状态 3 也是一个移进状态,所以下一个 (也被移进到栈中,而且在 (上的转换返回到状态 3。移进再 一次将a放入到栈中,而且 a上的转换由状态 3进入到状态 2。现在位于表 5 - 3的第4步,而且 已到达了第1个归约状态。这里的状态 2和符号a都是由栈弹出的,并回到处理中的状态 3。接 着,将A压入到栈中,且得到由状态 3到状态4的A转换。状态 4是一个移进状态,所以 )被移 进到栈中,且 )上的转换使分析转到状态 5。这里发生了一个由规则 A→ ( A ) 进行的归约, 它从栈中弹出状态 5、状态 4、状态3以及符号)、A和)。现在的分析位于状态 3中,而且A和 1 5 8 编译原理及实践 下载

China-pub.com 第5章自底向上的分析 159 下载 状态4又被压入到栈中。)再一次被移进到栈中,且压入状态5。由4一(A)进行的另一个 归约从栈中(向后地)别除了串(3A4)5,而将分析留在状态0中。现在A已被压入且也得到 了由状态0到状态1的4转换。状态1是接受状态。由于输入现在是空的,则分析算法承认它。 A'→,A a. ② A A一⊙ 图55例5.9的项目集合的DFA 表5-3例5.9的分析动作 分析栈 输入 动作 $0 ((a))s 移进 2 s0(3 (a))s 移进 3 $0(3(3 a))$ 移 50(3(3a 用一a归的 $0(3(3A4 )) 6 $0(3(3A4)5 )$ 用A一(A)归约 7 50《3A4 )5 移进 8 s0(3A3)5 (4)归约 9 80A1 $ 接受 也可将项目集合的DFA以及由LR(O)分析算法指定的动作合并到分析表中,所以LR(O) 分析就变成一个表驱动的分析方法了。其典型结构是:表的每行用DFA的状态标出,而每 一个列也如下标出。由于LR(O)分析状态是“移进的”状态或“归约的”状态,所以专门利 用一列来为每个状态指出它。若是“归约的”状态,就用另一个列来指出在归约中所使用 的文法规则选择。若是移进的状态,将被移进的符号会判断出下一个状态(通过DFA),所 以每个记号都会有一个列,而这些记号的各项都是有关该记号移进后将移到的新状态。由 于不能在输入中真正地看到它们,所以尽管分析程序的行为好像是它们被移进了,非终结 符上的转换(在归约时被压入)仍代表着一个特殊情况。因此,在“移进的”状态中还需要 为每个非终结符有一个列,而且按照惯例,这些列被列入到称为g0部分的表的一个单独 部分中。 表54就是这样的分析表的一个例子,它是例5.9中文法的表格。读者可以证实这个表将引 出如在表5-3中给出的示例的分析动作
状态4又被压入到栈中。 )再一次被移进到栈中,且压入状态 5。由A→ ( A ) 进行的另一个 归约从栈中(向后地)删除了串( 3 A 4 ) 5,而将分析留在状态 0中。现在A已被压入且也得到 了由状态0到状态1的A转换。状态1是接受状态。由于输入现在是空的,则分析算法承认它。 图5-5 例5 . 9的项目集合的D FA 表5-3 例5 . 9的分析动作 分 析 栈 输 入 动 作 1 $ 0 ( ( a ) ) $ 移进 2 $ 0 ( 3 ( a ) ) $ 移进 3 $ 0 ( 3 ( 3 a ) ) $ 移进 4 $ 0 ( 3 ( 3 a 2 ) ) $ 用A→ a归约 5 $ 0 ( 3 ( 3 A 4 ) )$ 移进 6 $ 0 ( 3 ( 3 A 4 ) 5 ) $ 用A→ ( A ) 归约 7 $ 0 ( 3 A 4 ) $ 移进 8 $ 0 ( 3 A 3 ) 5 $ 用A→ ( A ) 归约 9 $ 0 A 1 $ 接受 也可将项目集合的 D FA以及由L R ( 0 )分析算法指定的动作合并到分析表中,所以 L R ( 0 ) 分析就变成一个表驱动的分析方法了。其典型结构是:表的每行用 D FA的状态标出,而每 一个列也如下标出。由于 L R ( 0 )分析状态是“移进的”状态或“归约的”状态,所以专门利 用一列来为每个状态指出它。若是“归约的”状态,就用另一个列来指出在归约中所使用 的文法规则选择。若是移进的状态,将被移进的符号会判断出下一个状态 (通过D FA ),所 以每个记号都会有一个列,而这些记号的各项都是有关该记号移进后将移到的新状态。由 于不能在输入中真正地看到它们,所以尽管分析程序的行为好像是它们被移进了,非终结 符上的转换 (在归约时被压入 )仍代表着一个特殊情况。因此,在“移进的”状态中还需要 为每个非终结符有一个列,而且按照惯例,这些列被列入到称为 g o t o部分的表的一个单独 部分中。 表5 - 4就是这样的分析表的一个例子,它是例 5 . 9中文法的表格。读者可以证实这个表将引 出如在表5 - 3中给出的示例的分析动作。 第 5章 自底向上的分析 1 5 9 下载