
4.2自底向上的语法分析 ·自底向上()的语法分析是从给定的符号串出发,试图逐步 将它们归约为文法的开始符号 ·个的语法分析采用的是最左(规范)归约 ·本节中介绍两种个分析方法,即优先分析法和LR分析法; 。 ↑分析也需要一个分析栈用于存放分析过程中所得的文法 符号,开始时,先将#入栈,然后逐步地将输入符号移进栈,当 句柄在栈顶形成时,则进行归约,否则移进下一符号在分析 的每一步,分析动作都是由当前栈里的内容和扫描到的符 号确定的 ·分析动作有:移进,归约,报错,接受
4.2 自底向上的语法分析 • 自底向上()的语法分析是从给定的符号串出发,试图逐步 将它们归约为文法的开始符号. • 的语法分析采用的是最左(规范)归约 • 本节中介绍两种分析方法,即优先分析法和LR分析法; • 分析也需要一个分析栈用于存放分析过程中所得的文法 符号,开始时,先将#入栈,然后逐步地将输入符号移进栈,当 句柄在栈顶形成时,则进行归约,否则移进下一符号.在分析 的每一步,分析动作都是由当前栈里的内容和扫描到的符 号确定的. • 分析动作有:移进,归约,报错,接受
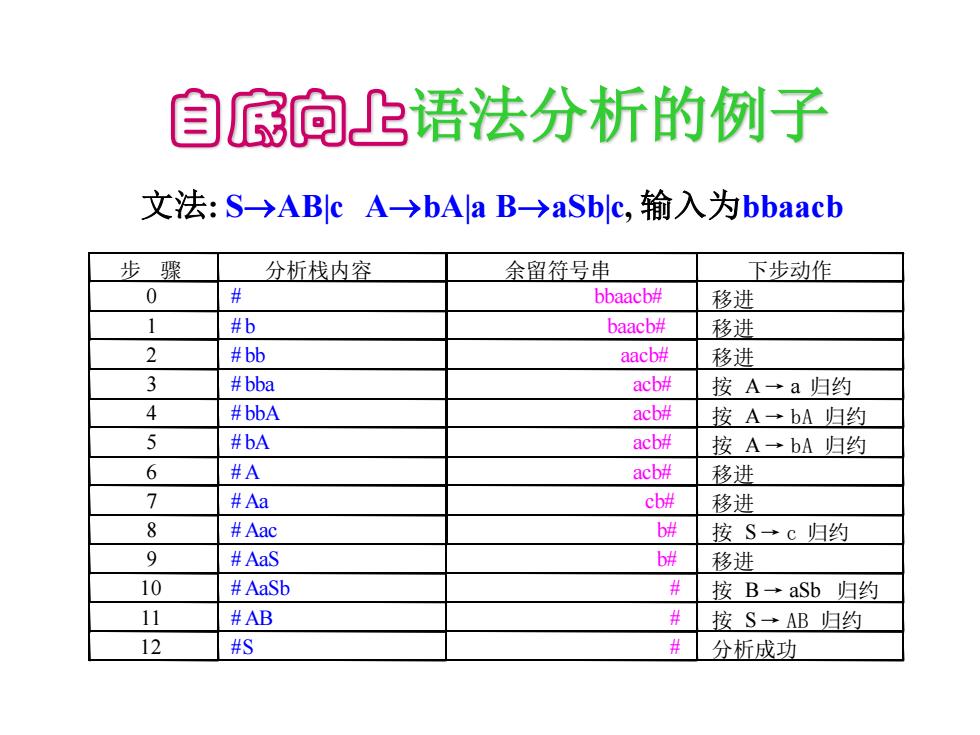
自底向上语法分析的例子 文法:S-→ABc A→bAaB→aSblc,输入为bbaacb 步骤 分析栈内容 余留符号串 下步动作 0 # bbaacb# 移进 1 #b baacb# 移进 2 #bb aacb# 移进 3 #bba acb# 按A→a归约 4 #bbA acb# 按A→bA归约 5 #bA acb# 按A→bA归约 6 #A acb# 移进 7 #Aa cb# 移进 8 #Aac b 按S→c归约 9 #AaS b# 移进 10 #AaSb #按B→aSb归约 11 #AB 按S→AB归约 12 #S 分析成功
文法: S→AB|c A→bA|a B→aSb|c, 输入为bbaacb 自底向上语法分析的例子 步 骤 分析栈内容 余留符号串 下步动作 0 # bbaacb# 移进 1 # b baacb# 移进 2 # bb aacb# 移进 3 # bba acb# 按 A→ a 归约 4 # bbA acb# 按 A→ bA 归约 5 # bA acb# 按 A→ bA 归约 6 #A acb# 移进 7 #Aa cb# 移进 8 #Aac b# 按 S→ c 归约 9 #AaS b# 移进 10 #AaSb # 按 B→ aSb 归约 11 #AB # 按 S→ AB 归约 12 #S # 分析成功

关于自底向上分析 ·分析过程是最左归约的(规范的): ·注意,在分析过程中,一旦句柄在栈顶形成,则立即 归约; ·有时栈顶出现了某产生式的右部,但它不一定是句 柄(如前例中第七步,栈顶的a并不是句柄); 从分析过程可容易地建立一棵语法树,可用作语法 分析的输出.建立树的方法见P127,这里从略
关于自底向上分析 • 分析过程是最左归约的(规范的); • 注意,在分析过程中,一旦句柄在栈顶形成,则立即 归约; • 有时栈顶出现了某产生式的右部,但它不一定是句 柄(如前例中第七步,栈顶的a并不是句柄); • 从分析过程可容易地建立一棵语法树,可用作语法 分析的输出.建立树的方法见P127,这里从略

4.2.1简单优先分析法 ·方法:在文法的符号之间建立一套(实际是三 种)优先关系RcV×V,在分析的过程中,利用 优先关系的比较,来确定当前句型的句柄: ·在找到句柄后按相应的产生式归约之,并将 归约出的V符号压入栈,再进行新的比较,如 此工作下去,直到出错或分析成功:
4.2.1 简单优先分析法 • 方法:在文法的符号之间建立一套(实际是三 种)优先关系RVV,在分析的过程中,利用 优先关系的比较,来确定当前句型的句柄; • 在找到句柄后按相应的产生式归约之,并将 归约出的VN符号压入栈,再进行新的比较,如 此工作下去,直到出错或分析成功

(一)简单优先关系的定义 设G是已化简的文法,s,teV,若G中存在规范句型o=.st.,则 s,t与的句柄之间的关系必有下述情况之一: .S t 。,。 。。。 st.. 1.s在句柄中, 2.s与t均在句 3.s不在句柄中,而t 而不在句柄中 柄中 在句柄中 对于上述情况,我们规定,情况1:s>t;情况2:s=t; 情况3:s<t 另外,还有一种情况,就是s和均不在句柄中,那么一定存在某个 句型使得它们进入上述三种情况之一. 若s和在任何句型中都不可能相邻出现,则我们规定二者无关系 注意,这种优先关系是不对称的:
(一)简单优先关系的定义 • 设G是已化简的文法,s,tV,若G中存在规范句型 =…st…, 则 s,t与的句柄之间的关系必有下述情况之一: A … … s t ... 1. s在句柄中, 而t不在句柄中 A … … s t … ... 2. s与t均在句 柄中 A … … s t … ... 3. s不在句柄中,而t 在句柄中 对于上述情况,我们规定,情况1: s>t; 情况2: s=t; 情况3: s<t 另外,还有一种情况,就是s和t均不在句柄中,那么一定存在某个 句型使得它们进入上述三种情况之一. 若s和t在任何句型中都不可能相邻出现,则我们规定二者无关系. 注意,这种优先关系是不对称的!

简单优光文法的定义 定义4.1 若一文法G的任何两个符号之间至多存在一种 优先关系,且任意两个不同的产生式无相同的右部,则称G 为简单优先文法 例4.4考虑文法GE: E=>E>E红1>E+T E→E1E1→E1+T1T1T1→T =>E+T*F=>E1+T*i T→T*F叫FF→(E)川i =>E+E*i=>E+i*i 由文法的产生式可直接看出: E=>E1=>I1=>I=>T*E=> T*E)=>T*(E)=>T*E1工) E1=+;+=T1;T=*;*=F;(=E; E-) 从相应的语法树不难看出,+, +*,F>*,*<i,以及: 考查句型E+i*i及T*(E+T) *<(,(E,EP),TP)
简单优先文法的定义 定义4.1 若一文法G的任何两个符号之间至多存在一种 优先关系,且任意两个不同的产生式无相同的右部,则称G 为简单优先文法 例4.4考虑文法G’[E]: E→E1 E1→E1+T1 |T1 T1→T T→T*F | F F→(E) | i 由文法的产生式可直接看出: E1 = +; +=T1 ; T = *; * = F; (=E; E=) 考查句型 E1+i*i 及 T*(E1+T1 ) E=>E1=>E1+T1=>E1+T =>E1+T*F =>E1+T*i =>E1+F*i =>E1+i*i E=> E1=> T1=> T =>T*F => T*(E) =>T*(E1 ) =>T*(E1+T1 ) 从相应的语法树不难看出, +*, F>*, *), T1>)
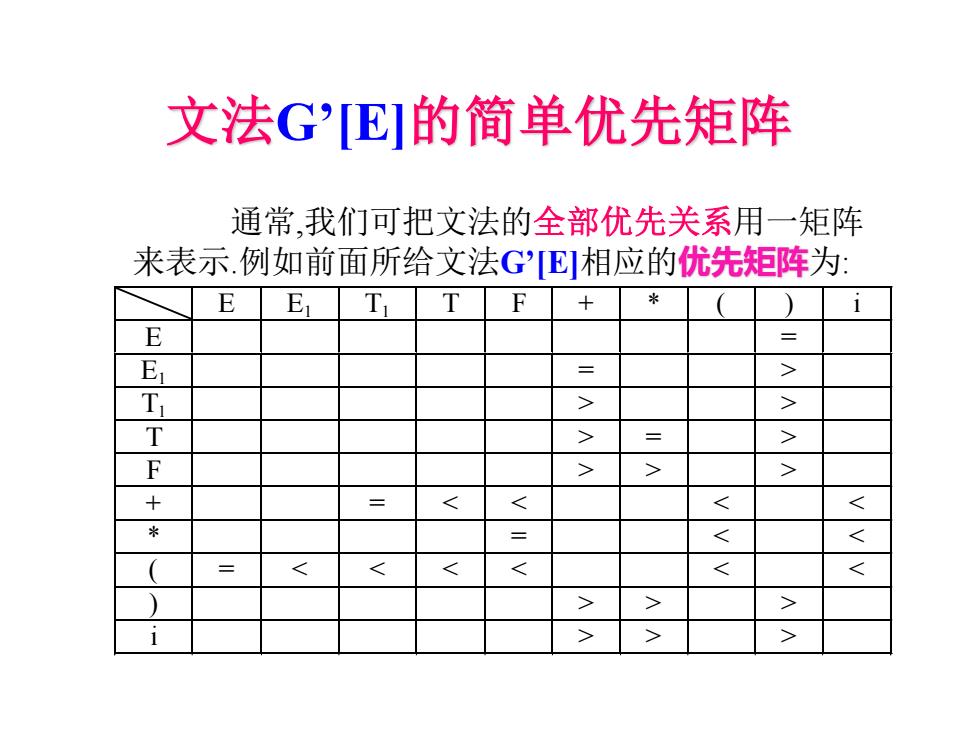
文法GE]的简单优先矩阵 通常,我们可把文法的全部优先关系用一矩阵 来表示.例如前面所给文法GE相应的优先矩阵为: E T F + E Er T > > T > = > F > + > 1 > 7 >
E E1 T1 T F + * ( ) i E = E1 = > T1 > > T > = > F > > > + = > > i > > > 文法G’[E]的简单优先矩阵 通常,我们可把文法的全部优先关系用一矩阵 来表示.例如前面所给文法G’[E]相应的优先矩阵为:

(二)简单优先分析的算法 ·利用优先矩阵进行分析的方法是,逐次查看当前句型 X1X2.X相邻两个符号的优先关系,一旦出现 X+k之X+k+1,X+k即为句柄的尾符号,然后从X+k开始向 左查看已扫描过的符号,直到发现X1<X,X即为句柄的 头符号. ·可以证明,X到X+k之间的符号恰好构成了当前句型的 句柄. ·简单优先分析的驱动程序见下页
(二) 简单优先分析的算法 • 利用优先矩阵进行分析的方法是,逐次查看当前句型 X1X2…Xm相邻两个符号的优先关系,一旦出现 Xi+k>Xi+k+1, Xi+k即为句柄的尾符号,然后从Xi+k开始向 左查看已扫描过的符号,直到发现Xi-1<Xi ,Xi即为句柄的 头符号. • 可以证明, Xi到Xi+k 之间的符号恰好构成了当前句型的 句柄. • 简单优先分析的驱动程序见下页

程序4-4简单优先分析驱动程序 int parser(void){ if(LeftSide){/*LeftSide!=0 int i=0,k=0,r;stack[0]='#; means the production exists * r=a[k++]; do{intj,LeftSide; i=j;stack[i]=LeftSide; while(!lsHigherThan(stack[i],r)) Jelse /There is no production which matches {stack[++=r;r=a[k++];> the right side * j=i; if(i==2&&r=='#&&stack[i] while(!IsLowerThan == STARTSYSBOL) (stack[j-1],stack[j]))j--j return SUCCESS; LeftSide= else return ERROR; RightSideOfAProduction (stack[],stack[i],i-j+1); }while (1); }/end of parser*
程序4-4 简单优先分析驱动程序 int parser(void){ int i=0,k=0,r;stack[0]='#'; r=a[k++]; do{ int j,LeftSide; while(!IsHigherThan(stack[i],r)) {stack[++i]=r;r=a[k++];} j=i; while(!IsLowerThan (stack[j-1], stack[j])) j--; LeftSide= RightSideOfAProduction (stack[j],stack[i],i-j+1); if(LeftSide){ /*LeftSide!=0 means the production exists */ i=j;stack[i]=LeftSide; }else /* There is no production which matches the right side */ if(i==2 && r=='#' && stack[i] == STARTSYSBOL) return SUCCESS; else return ERROR; } while (1); } /* end of parser */
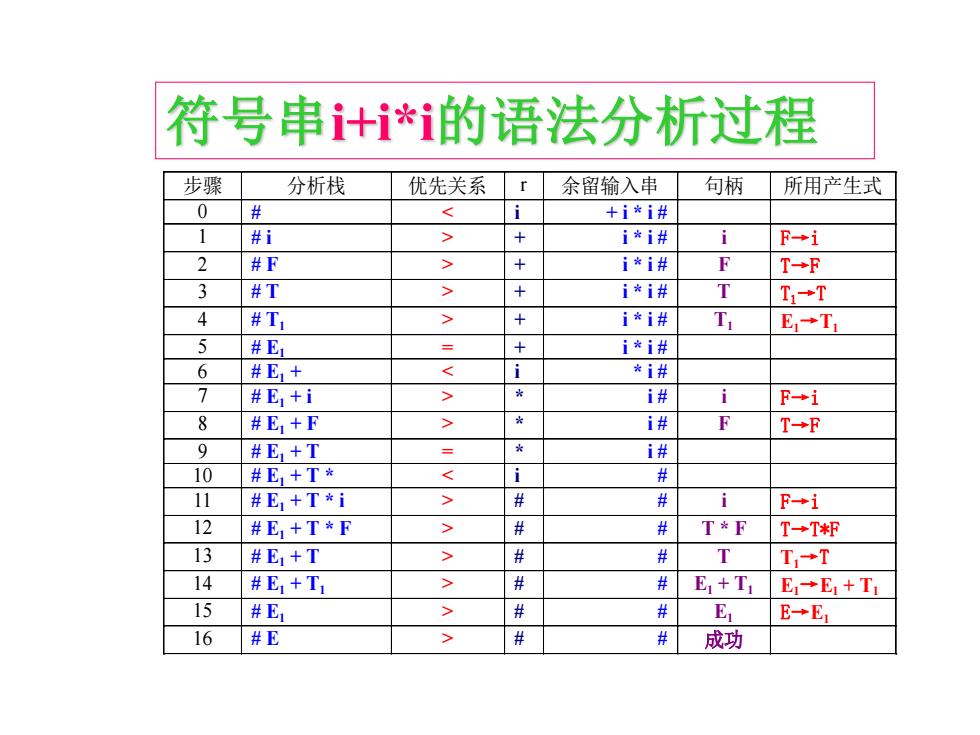
符号串+i*的语法分析过程 步骤 分析栈 优先关系 余留输入串 句柄 所用产生式 0 # i +i*i# 1 #i > + i*i# i F→i 2 #F > i*i# F T→F 3 #T > i*i# T T1→T 4 #T1 > i*i# Tu E,→T1 5 #E1 + i*i# 6 #E1+ ★ i# i F-i 8 #E1+F > i# F T→F 9 #E1+T i# 10 #E1+T* # # T*F T→T*却 13 #E1+T > 杂 件 T T,→T 14 #E1+T1 # 必 E1+T1 E→E1+T1 15 #E > # E E→E1 16 #E > # 成功
步骤 分析栈 优先关系 r 余留输入串 句柄 所用产生式 0 # + i * i # i F→i 2 # F > + i * i # F T→F 3 # T > + i * i # T T1→T 4 # T1 > + i * i # T1 E1→T1 5 # E1 = + i * i # 6 # E1 + * i # i F→i 8 # E1 + F > * i # F T→F 9 # E1 + T = * i # 10 # E1 + T * # # i F→i 12 # E1 + T * F > # # T * F T→T*F 13 # E1 + T > # # T T1→T 14 # E1 + T1 > # # E1 + T1 E1→E1 + T1 15 # E1 > # # E1 E→E1 16 # E > # # 成功 符号串i+i*i的语法分析过程