
4.2.4 LR分析法 ·迄今为止我们所学的分析方法对文法都有一定的要求,即 有局限性; ·1965年D.Knuth提出了分析效率极高的LR(k)分析技术; ·LR分析:自左至右扫描的自底向上的分析; 在分析的每一步,只须根据分析栈中的已移进的和已归约 出的符号,并至多向前扫描k个字符就能确定应采取什么分 析动作(移进、归约、接受、报错): ·LR分析对文法要求很少,效率极高,且能及时发现错误,是目 前最广泛使用的方法,一般用CFG描述的的程序设计语言 只需稍加一些辅助功能即可用LR分析法实现编译程序
4.2.4 LR分析法 • 迄今为止我们所学的分析方法对文法都有一定的要求,即 有局限性; • 1965年D.Knuth提出了分析效率极高的LR(k)分析技术; • LR分析: 自左至右扫描的自底向上的分析; • 在分析的每一步,只须根据分析栈中的已移进的和已归约 出的符号,并至多向前扫描k个字符就能确定应采取什么分 析动作(移进、归约、接受、报错); • LR分析对文法要求很少,效率极高,且能及时发现错误,是目 前最广泛使用的方法;一般用CFG描述的的程序设计语言 只需稍加一些辅助功能即可用LR分析法实现编译程序

LR分析综述 ·计算机理论研究已证明了如下结论: ·LR(K)文法是无二义性文法; ·LR(k)文法与LR(1)文法等价: 由于常见的程序设计语言均能由LR(1)文法产生,因此我们只讨论k=0,1 两种情况; ·本节中,我们将先介绍LR分析器的逻辑结构及工作原理,再分别介绍几 种LR分析器(即LR(O),SLR(1),LR(1)和LALR(1)的构造; ·LR(O)简单,能力低;SLR(1)能力强于LR(O);LR(1)能力强,但分析表 大; ·LALR(1)能力介于SLR(1)与LR(1)之间,表大小与SLR(1)相同,是最常用 的分析方法
LR分析综述 • 计算机理论研究已证明了如下结论: • LR(k)文法是无二义性文法; • LR(k)文法与LR(1)文法等价. • 由于常见的程序设计语言均能由LR(1)文法产生,因此我们只讨论k=0,1 两种情况; • 本节中,我们将先介绍LR分析器的逻辑结构及工作原理,再分别介绍几 种LR分析器(即LR(0),SLR(1),LR(1)和LALR(1))的构造; • LR(0)简单,能力低; SLR(1)能力强于LR(0); LR(1)能力强,但分析表 大; • LALR(1)能力介于SLR(1)与LR(1)之间,表大小与SLR(1)相同,是最常用 的分析方法
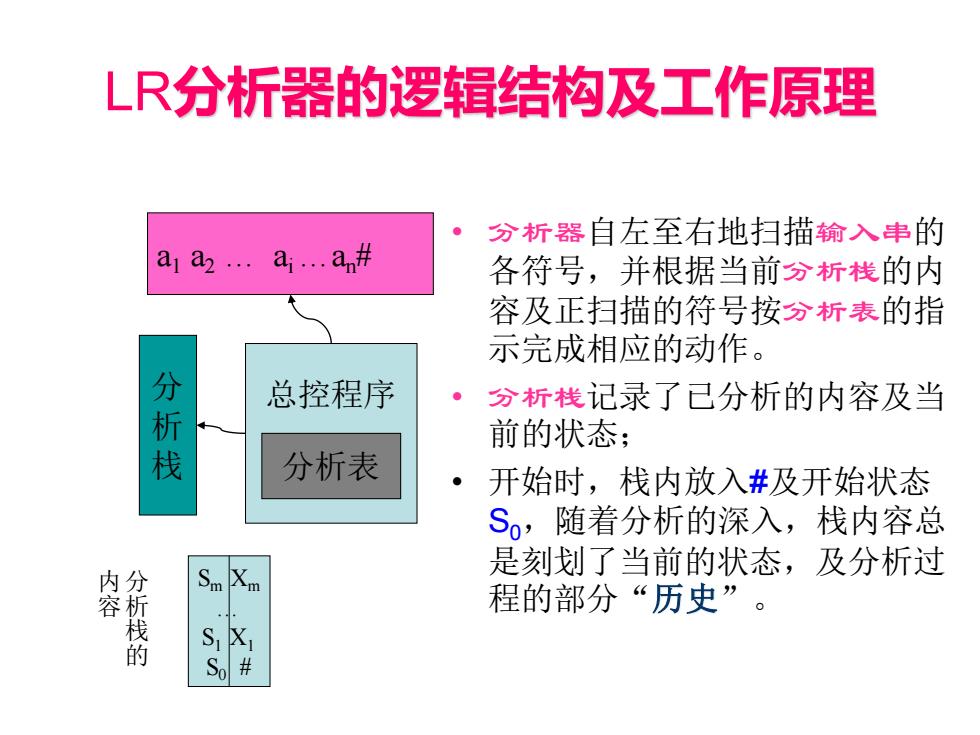
LR分析器的逻辑结构及工作原理 分析器自左至右地扫描输入串的 al a...ai...a# 各符号,并根据当前分析栈的内 容及正扫描的符号按分析表的指 示完成相应的动作。 分 总控程序 分析栈记录了已分析的内容及当 祈栈 前的状态: 分析表 开始时,栈内放入#及开始状态 S,随着分析的深入,栈内容总 是刻划了当前的状态,及分析过 分析栈的 Xm 程的部分“历史”。 S
LR分析器的逻辑结构及工作原理 • 分析器自左至右地扫描输入串的 各符号,并根据当前分析栈的内 容及正扫描的符号按分析表的指 示完成相应的动作。 • 分析栈记录了已分析的内容及当 前的状态; • 开始时,栈内放入#及开始状态 S0,随着分析的深入,栈内容总 是刻划了当前的状态,及分析过 程的部分“历史”。 总控程序 分析表 分 析 栈 a1 a2 … ai …an# Sm Xm … S1 X1 S0 # 分 析 栈 的 内 容
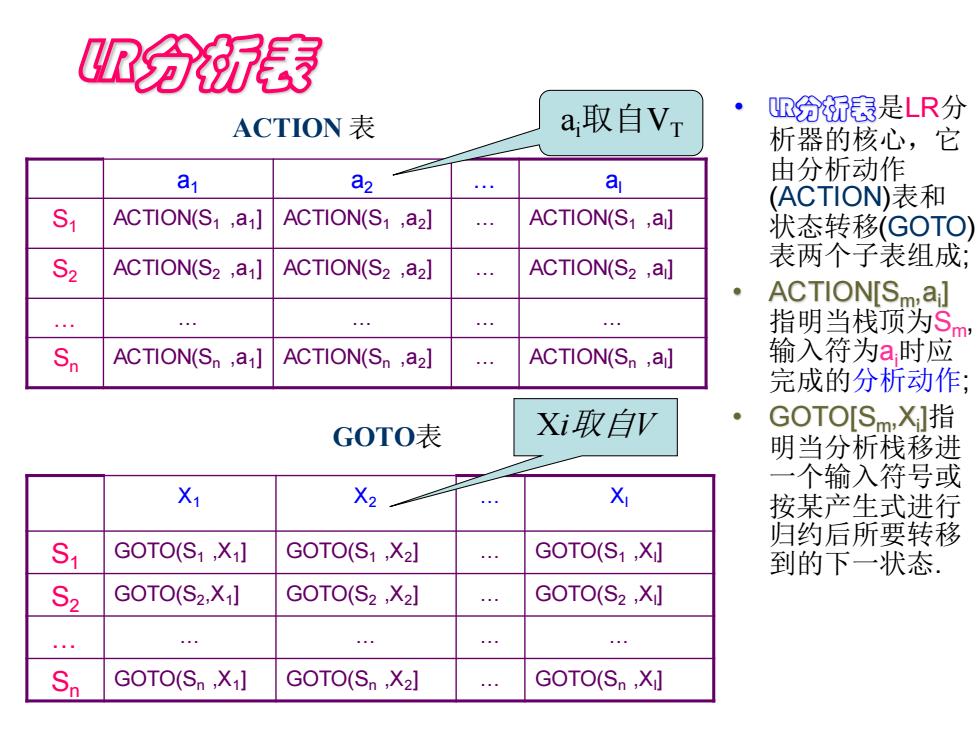
R分行表 R分析表是LR分 ACTION表 a取自Vt 析器的核心,它 a a2 a 由分析动作 (ACTION)表和 S1 ACTION(S1 ,a] ACTION(S1 ,a2] ACTION(S ,ai] 状态转移GOTO) S2 ACTION(S2,a] ACTION(S2 ,a2] ACTION(S2 ,ai] 表两个子表组成; ACTION[Sm.ai] 指明当栈顶为Sm, Sn ACTION(Sn,a] ACTION(Sn ,a2] ACTION(Sn,ai] 输入符为a时应 完成的分析动作: G0TO表 Xi取自V GOTO[Sm,X]指 明当分析栈移进 个输入符号或 X1 X2 X 按某产生式进行 S 归约后所要转移 GOTO(S1 ,Xi] GOTO(S1 ,X2] GOTO(S ,X] 到的下一状态. S2 GOTO(S2.Xi] GOTO(S2 ,X2] GOTO(S2 ,Xi] . … … … Sn GOTO(Sn,X1] GOTO(Sn,X2] GOTO(S,Xi]
LR分析表 • LR分析表是LR分 析器的核心,它 由分析动作 (ACTION)表和 状态转移(GOTO) 表两个子表组成; • ACTION[Sm,ai ] 指明当栈顶为Sm, 输入符为ai时应 完成的分析动作; • GOTO[Sm,Xi ]指 明当分析栈移进 一个输入符号或 按某产生式进行 归约后所要转移 到的下一状态. a1 a2 … al S1 ACTION(S1 ,a1 ] ACTION(S1 ,a2 ] … ACTION(S1 ,al ] S2 ACTION(S2 ,a1 ] ACTION(S2 ,a2 ] … ACTION(S2 ,al ] … … … … … Sn ACTION(Sn ,a1 ] ACTION(Sn ,a2 ] … ACTION(Sn ,al ] X1 X2 … Xl S1 GOTO(S1 ,X1 ] GOTO(S1 ,X2 ] … GOTO(S1 ,Xl ] S2 GOTO(S2 ,X1 ] GOTO(S2 ,X2 ] … GOTO(S2 ,Xl ] … … … … … Sn GOTO(Sn ,X1 ] GOTO(Sn ,X2 ] … GOTO(Sn ,Xl ] ACTION 表 GOTO表 ai取自VT Xi取自V

LR分析器的工作过程 1.分析开始时,首先将初始状态 S0及#压入栈; SSIS2S 2.设在分析的某一步,分析栈和 余留输入串处于格局: #X X2...Xm aiaitiait2...a# 用ISma查ACTION表,并根据指示完 再用Sma查G0T0表,设得 成相应的动作,分析动作有移进,归约, Sm+,将Sm+1压入栈: 报错,接受四种: SOSSSSH [们移进表明句柄尚未在栈顶形成, 正期待继续移进输入符号以形成句 #X1X2...Xmai aitiai2...a# 柄,故将a压入栈: SS SS #X X2...Xmai ai+1ait2…an#
LR分析器的工作过程 1.分析开始时,首先将初始状态 S0及#压入栈; 2.设在分析的某一步,分析栈和 余留输入串处于格局: S0S1S2…Sm # X1X2…Xm aiai+1ai+2…an# 用(Sm,ai )查ACTION表,并根据指示完 成相应的动作,分析动作有移进,归约, 报错,接受四种: (1)移进 表明句柄尚未在栈顶形成, 正期待继续移进输入符号以形成句 柄,故将ai压入栈: S0S1S2…Sm # X1X2…Xmai ai+1ai+2…an# 再用Sm,ai 查GOTO表,设得 Sm+1,将Sm+1压入栈: S0S1S2…SmSm+1 # X1X2…Xmai ai+1ai+2…an#

LR分析器的工作过程(续) (2)归约斯其中r表示按P的第产生式 (3)若ACTION(Sm,a)=“acc”,则表明当 AXXX进行归约这表 前输入串已被成功地分析完毕,结 明栈顶部的符号串Xmm2Xm 是当前句型的句柄岿约的方法是, 束; 将栈顶符号串Xmw1Xm+2.Xmr个 (4)若ACTION(Sm,a)=“ERROR”,则表 符号及相应的状态Smr+1Smr2Sm) 明当前输入串有语法错误,转入出 从栈顶退出,再将A压入栈,此时的 错处理程序; 格局为 3.重复步骤2的工作,直到分析的某步 SoSISS 栈顶出现“acc”为止.此时的格局 X1X2...Xm-rA ajaitiait2...an 应为: 再以(Sm-eA)查GOTO表,得Sk将 Sk压入栈,得到格局: SoSz # #Z SOSISSm-Sk XiX2..Xm-rA aiai+iai+2...an# 其中,Z为文法的开始符号,S2是使 注意,完成归约动作时,输入串指针 ACTION(Sz,)=“acc”的唯一状态. 并未移动
LR分析器的工作过程(续) (2)归约rj 其中rj表示按P的第j产生式 A→Xm-r+1Xm-r+2Xm进行归约;这表 明栈顶部的符号串Xm-r+1Xm-r+2Xm 是当前句型的句柄.归约的方法是, 将栈顶符号串Xm-r+1Xm-r+2Xm(r个 符号及相应的状态Sm-r+1Sm-r+2Sm) 从栈顶退出,再将A压入栈,此时的 格局为 S0S1S2…Sm-r # X1X2… Xm-rA aiai+1ai+2…an# 再以(Sm-r ,A)查GOTO表,得Sk ,将 Sk压入栈,得到格局: S0S1S2…Sm-rSk # X1X2… Xm-rA aiai+1ai+2…an# 注意,完成归约动作时,输入串指针 并未移动. (3)若ACTION(Sm,ai )=“acc” ,则表明当 前输入串已被成功地分析完毕,结 束; (4)若ACTION(Sm,ai )=“ERROR” ,则表 明当前输入串有语法错误,转入出 错处理程序; 3. 重复步骤2.的工作,直到分析的某步, 栈顶出现“acc”为止.此时的格局 应为: S0SZ # # Z 其中,Z为文法 的开始符号, SZ是使 ACTION(SZ ,#)=“acc”的唯一状态
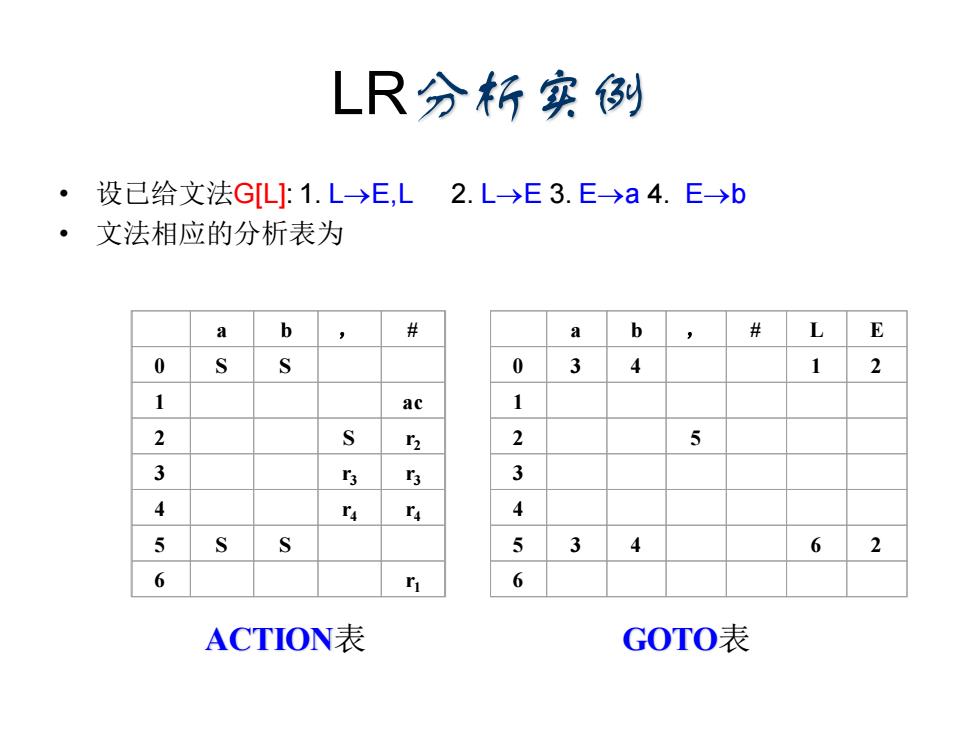
LR分析实例 ·设己给文法GL:1.L→E,L2.L→E3.E→a4.E→b ·文法相应的分析表为 a b a 6 L E 0 0 3 4 1 1 ac 1 2 r2 2 5 3 3 3 3 4 4 5 S 5 6 6 r 6 ACTION表 GOTO表
LR分析实例 • 设已给文法G[L]: 1. L→E,L 2. L→E 3. E→a 4. E→b • 文法相应的分析表为 a b , # 0 S S 1 ac 2 S r2 3 r3 r3 4 r4 r4 5 S S 6 r1 a b , # L E 0 3 4 1 2 1 2 5 3 4 5 3 4 6 2 6 ACTION表 GOTO表

分析表的合并 ·从分析表的功能及实例中,我们可看出,GOTO表中所有关于终结符的 状态转换都与相应的ACTION表相关,因此我们可将其合并到 ACTION表中,只将关于V符的状态转换保留在GOTO表中: 状 ACTION GOTO 女 在实际的分析表中,大 a LE S 12 多数表项内容为ERROR, 1 若略去不填,则分析表 ac 2 S5 r 是一稀疏表,可采用紧 3 r3 I3 凑的格式存储。 r ra 5 S3 6 2 6 r
分析表的合并 • 从分析表的功能及实例中,我们可看出,GOTO表中所有关于终结符的 状态转换都与相应的ACTION表相关,因此我们可将其合并到 ACTION表中,只将关于VN符的状态转换保留在GOTO表中: 状 态 ACTION GOTO a b , # L E 0 s3 s4 1 2 1 ac 2 s5 r2 3 r3 r3 4 r4 r4 5 s3 s4 6 2 6 r1 在实际的分析表中,大 多数表项内容为ERROR, 若略去不填,则分析表 是一稀疏表,可采用紧 凑的格式存储
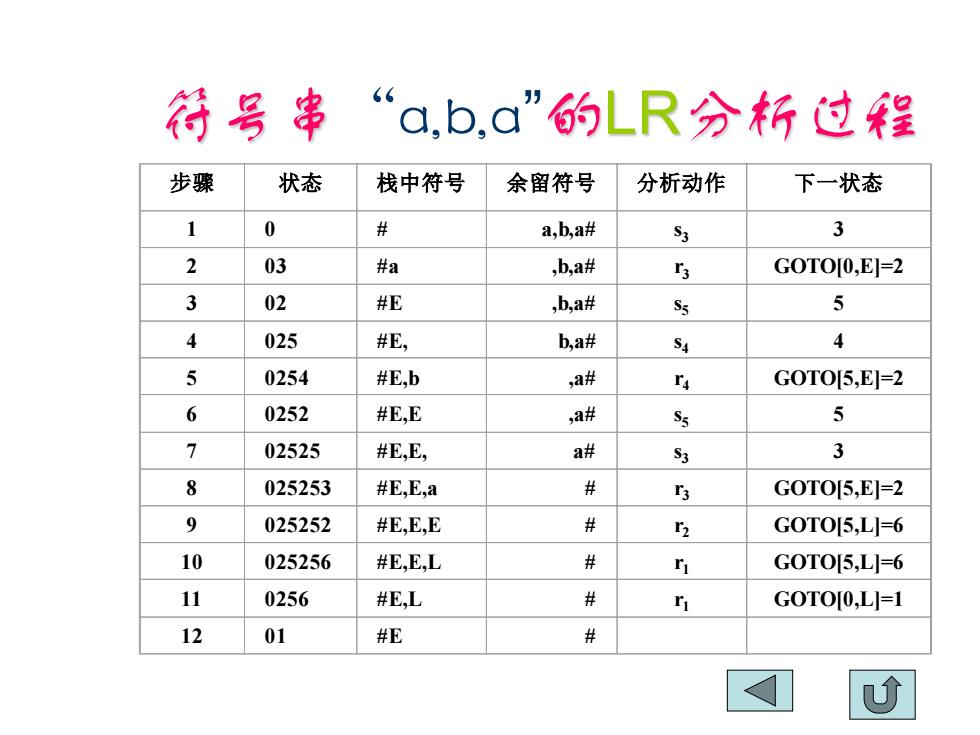
号串“a,b,a”的LR分析过程 步骤 状态 栈中符号 余留符号 分析动作 下一状态 1 0 井 a,b,a# S3 3 2 03 #a ,b,a# 5 G0T00,E]=2 3 02 #E ,b,a# S5 5 4 025 #E, b,a# S4 J 0254 #E,b ,a# r G0T05,E]=2 6 0252 #E,E ,a# S5 5 7 02525 #E,E, a# S3 3 8 025253 #E,E,a 女 3 G0T05,E]=2 9 025252 #E,E,E 井 2 G0T05,L=6 10 025256 #E,E,L 井 G0T05,L]=6 11 0256 #E,L # r G0T00,L=1 12 01 #E
符号串“a,b,a”的LR分析过程 步骤 状态 栈中符号 余留符号 分析动作 下一状态 1 0 # a,b,a# s3 3 2 03 #a ,b,a# r3 GOTO[0,E]=2 3 02 #E ,b,a# s5 5 4 025 #E, b,a# s4 4 5 0254 #E,b ,a# r4 GOTO[5,E]=2 6 0252 #E,E ,a# s5 5 7 02525 #E,E, a# s3 3 8 025253 #E,E,a # r3 GOTO[5,E]=2 9 025252 #E,E,E # r2 GOTO[5,L]=6 10 025256 #E,E,L # r1 GOTO[5,L]=6 11 0256 #E,L # r1 GOTO[0,L]=1 12 01 #E #

LR分析器的总控程序 ·parser()X ·初始化; while((item=ACTION[TopStat][InpSym]))!=Acc){ ● if(item==ERROR)error(); if(item==sj){push(j);advance();) else reduce(i);/*item==ri*/ ● accept();
LR分析器的总控程序 • parser( ){ • 初始化; • while((item=ACTION[TopStat][InpSym]))!=Acc){ • if(item==ERROR) error( ); • if(item==sj){push(j);advance( );} • else reduce(i);/* item== ri*/ • } • accept( ); • }