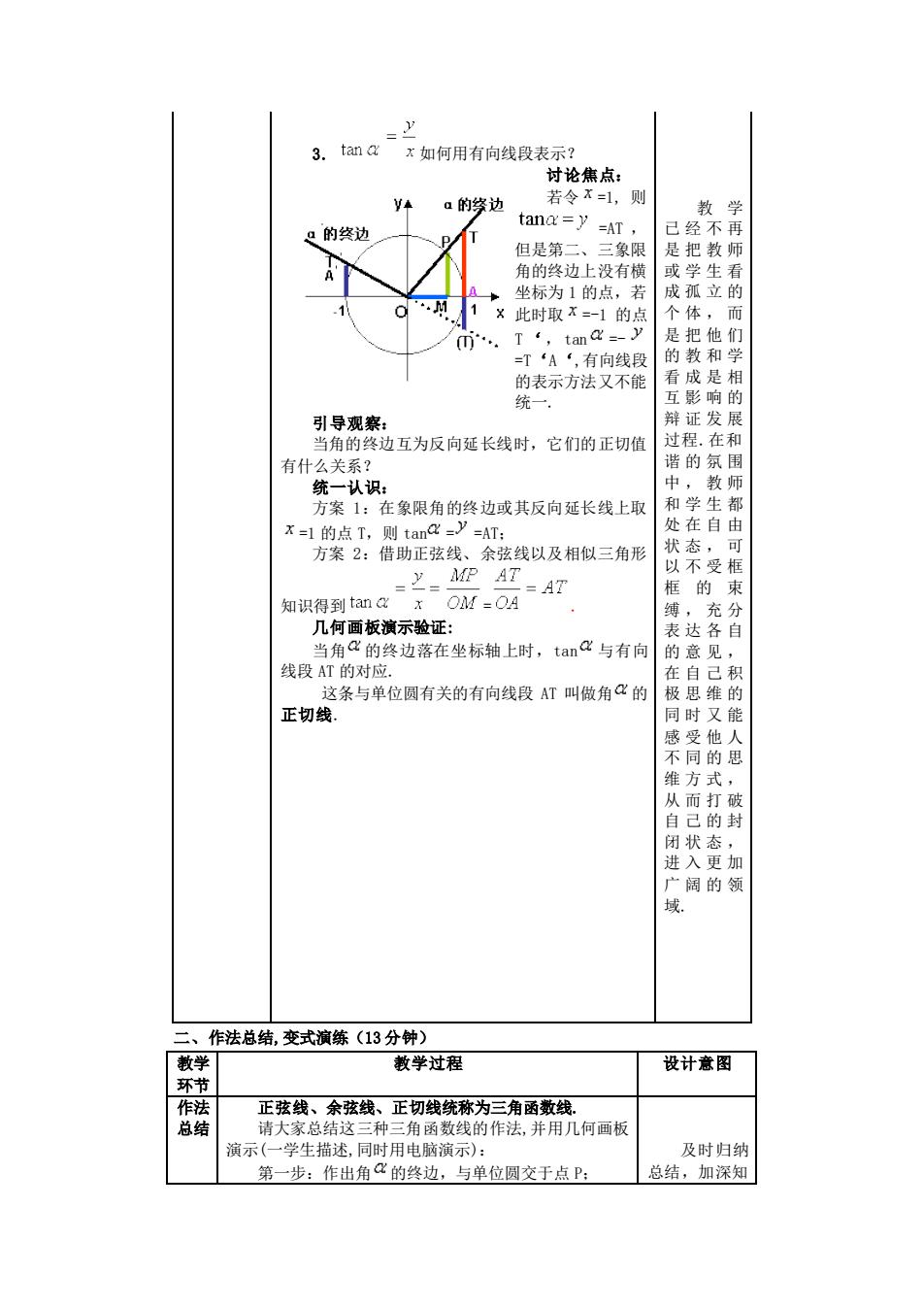
3. tan a x如何用有向线段表 讨论焦点： a的修边 若令x=1,则 Q的终边 tana=y =AT 是第 角 边上没有横 标为1的点， ×此时取x=一1的点 个体， ①. T,有向线段 看成是相 引导观察： 当角的终边互为反向延长线时，它们的正切值 有什么关系？ 统一认识： 方案1：在象限角的终边或其反向延长线上取 x=1的点T,则tan =AT: 方案2：借助正弦线、余弦线以及相似三角形 状态 以不受框 知识得到amO.OA 框的束 几何面板滴示验正： 终边落在坐标轴上时，tan与有向 线段AT的对 的 这条与单位圆有关的有向线段AT叫做角的 正切 维方式， 从而打破 自己的封 状态， 阔的领 域 作法总结，变式演练(13分钟) 教学 教学过程 设计意图 环节 正弦线、余弦线、正切线统称为三角函数线， 大家 三角函数线的作法，并用几何画板 步：作出角的终边，与单位圆交于点P 演示 生描述， 及时归纳 总结，加深知3. 如何用有向线段表示？ 讨论焦点： 若令 =1, 则 =AT ， 但是第二、三象限 角的终边上没有横 坐标为 1 的点，若 此时取 =-1 的点 T‘ ，tan =- =T‘A‘,有向线段 的表示方法又不能 统一. 引导观察： 当角的终边互为反向延长线时，它们的正切值 有什么关系？ 统一认识： 方案 1：在象限角的终边或其反向延长线上取 =1 的点 T，则 tan = =AT； 方案 2：借助正弦线、余弦线以及相似三角形 知识得到 = . 几何画板演示验证: 当角 的终边落在坐标轴上时，tan 与有向 线段 AT 的对应. 这条与单位圆有关的有向线段 AT 叫做角 的 正切线. 教 学 已经不再 是把教师 或学生看 成孤立的 个体，而 是把他们 的教和学 看成是相 互影响的 辩证发展 过程.在和 谐的氛围 中，教师 和学生都 处在自由 状态，可 以不受框 框的束 缚，充分 表达各自 的意见， 在自己积 极思维的 同时又能 感受他人 不同的思 维方式， 从而打破 自己的封 闭状态， 进入更加 广阔的领 域. 二、作法总结,变式演练（13 分钟） 教学 环节 教学过程 设计意图 作法 总结 正弦线、余弦线、正切线统称为三角函数线. 请大家总结这三种三角函数线的作法,并用几何画板 演示(一学生描述,同时用电脑演示)： 第一步：作出角 的终边，与单位圆交于点 P； 及时归纳 总结，加深知