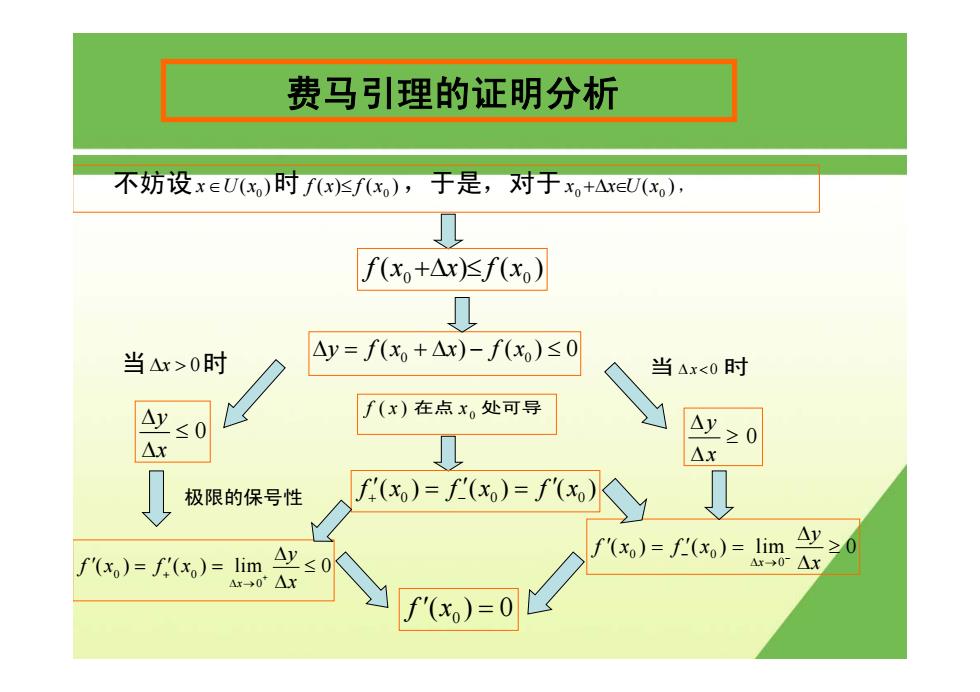
费马引理的证明分析 不妨设xEU(x,)时fx)sfx),于是，对于x。+△xEU(x), L f(x+△x)f(x) 见 当△x>0时 △y=f(x+△x)-f(x)≤0 当Ax<0时 △y ∫(x)在点x。处可导 ≤0 △x △x 极限的保号性 f()=f)=f'() f(xo)=f(xo)=lim Ay 20 f(x)=f(xo)=lim ≤0 △r→0-△x 4x0△x f'(x)=0不妨设 0 x∈U x( )时 ( ) ( ) 0 f x ≤ f x ，于是，对于 ( ) 0 0 x +Δx∈U x ， 费马引理的证明分析 ( ) ( ) 0 0 f x +Δx ≤ f x 当Δx > 0时 0 y x Δ ≤ Δ 0 0 0 ( ) ( ) lim 0 x y fx fx x + + Δ → Δ ′ ′ == ≤ Δ 0 y x Δ ≥ Δ 极限的保号性 当Δ x < 0 时 0 0 0 ( ) ( ) lim 0 x y fx fx x − − Δ → Δ ′ ′ = = ≥ Δ f ′(x0 ) = 0 0 0 Δy fx x fx = +Δ − ≤ ( ) ()0 f ( ) x 在点 0 x 处可导 0 00 f () () () x fx fx + − ′ = ′ ′ =