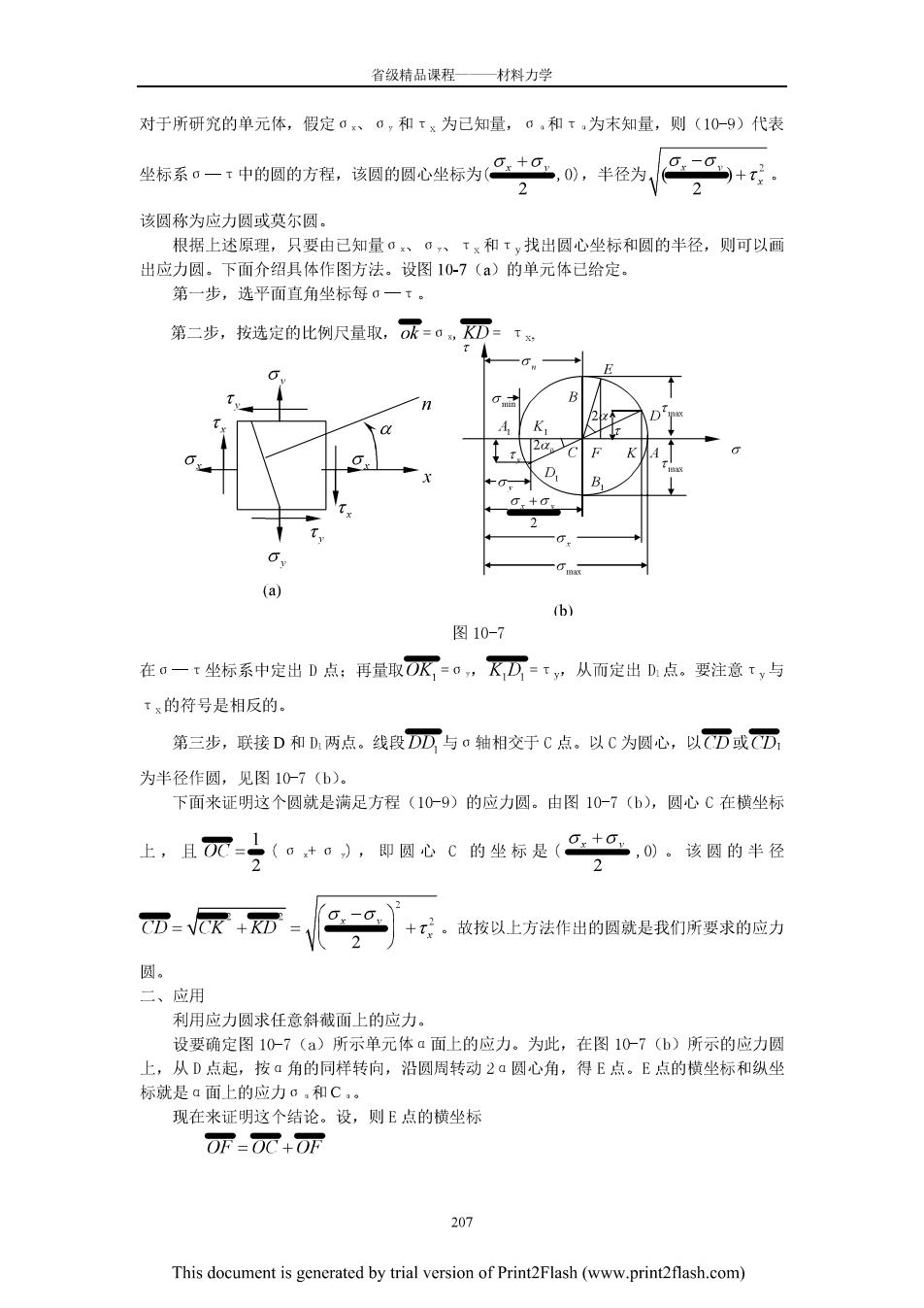
省领精品课程 一材料力学 对于所研究的单元体，假定a0,和tx为已知量，0，和t,为末知量，则(10-9)代表 坐标系0一：中的圆的方程，该圆的心坐标为巴，0，半径为，@+ 2 2 该圆称为应力圆或莫尔圆。 根据上述原理，只要由已知量·、a,Tx和T,找出圆心坐标和圆的半径，则可以画 出应力圆，下面介绍具体作图方法，设图10-7()的单元体已给定， 第一步，选平面直角坐标每0一t 第二步，按选定的比例尺量取，=0，⑦=T (b) 图10-7 在a一T坐标系中定出D点：再量取OK=o,KD=下，从而定出D点。要注意ty与 Tx的符号是相反的 第三步，联接D和D两点。线段DD与a轴相交于C点.以C为圆心，以CD或D 为半径作圆，见图107(b)。 下面来证明这个圆就是满足方程(109)的应力圆。由图10-7(b),圆心C在横坐标 上，且T(。+。),即圆心C的坐标是(+,0.该圆的半径 2 +。故按以上方法作出的圆就是我们所要求的应力 2 二、应用 利用应力圆求任意斜截面上的应力。 设要确定图10-7(a)所示单元体ū面上的应力。为此，在图10-7(b)所示的应力圆 上，从D点起，按a角的同样转向，沿圆周转动2a圆心角，得E点。E点的横坐标和纵坐 标就是a面上的应力c,和C, 现在来证 这个结论。设，则E点的横坐标 OF=OC+OF 207 This document is generated by trial version of Print2Flash(www.printflash.com)