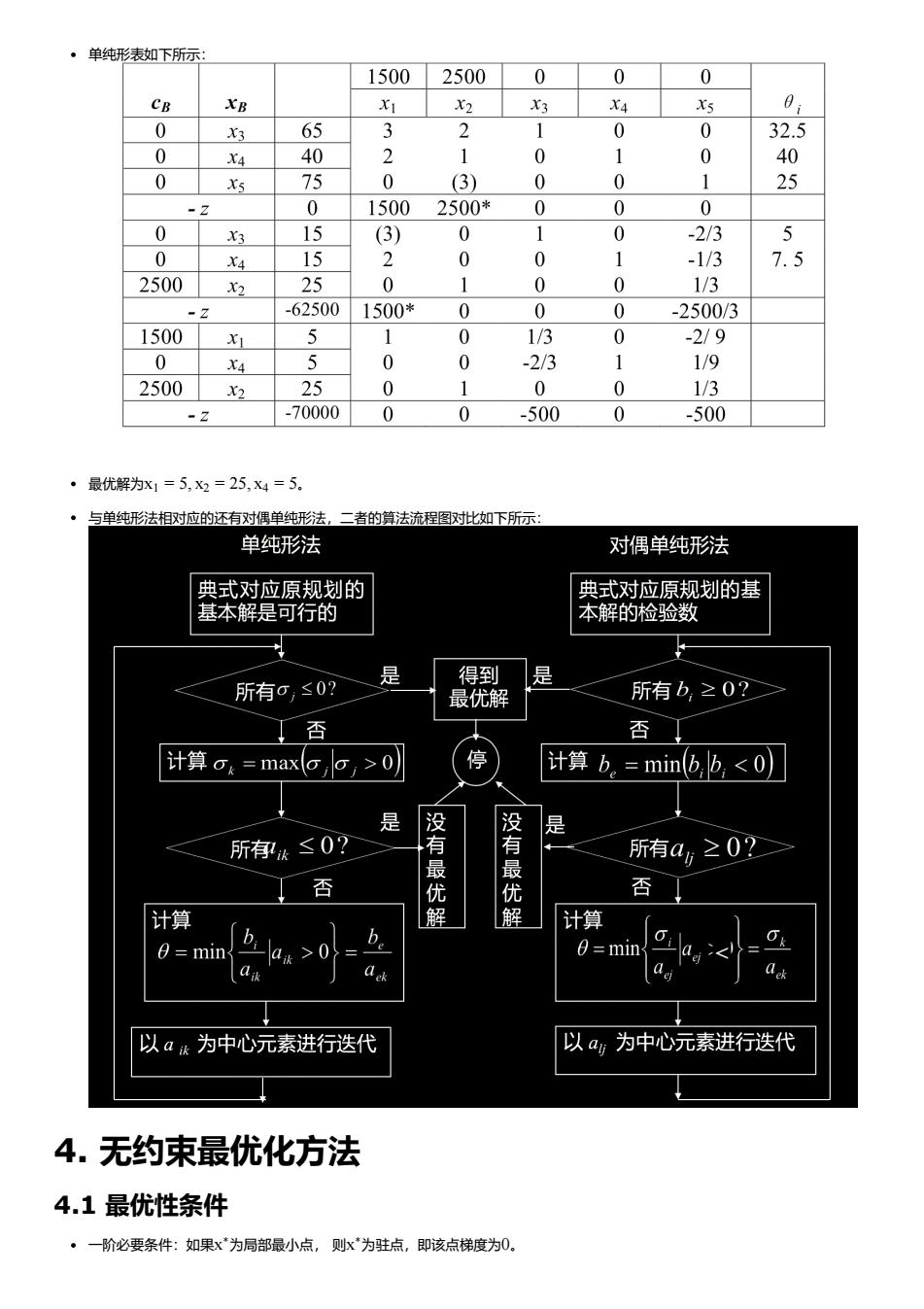
·单纯形表如下所示 1500 2500 0 0 0 CR XR Xs 65 0 40 32 0 0 32.5 0 40 0 75 0 (3) 0 0 25 0 1500 2500* 0 0 X3 15 (3) 0 -2/3 5 0 X4 15 0 -1/3 7.5 2500 25 0 1/3 -625001500* 0 0 0 -2500/3 1500 5 0 1/3 0 -2/9 0 0 0 -23 1 4 1/9 2500x2 25 0 0 0 1/3 -z -700000 0 -500 0 -500 ·最优解为x1=5,X2=25,x4=5 与单纯形法相对应的还有对偶单纯形法 二者的算法流程图对比如下所示 单纯形法 对偶单纯形法 典式对应原规划的 典式对应原规划的基 基本解是可行的 本解的检验数 所有0，≤0？ 、是 得到是 最优解 <所有b,20? 丁否 否] 计算g4=maxg,g,>0） 停 计算b.=minb,b,<0) 是 没 所存k≤0？ 所有a,≥0？> 优 计算 解 计算 0=min b b a> a 以a法为中心元素进行迭代 以a为中心元素进行迭代 4.无约束最优化方法 4.1最优性条件 ·一阶必要条件：如果x为局部最小点，则x为驻点，即该点梯度为0. 单纯形表如下所示： 最优解为 。 与单纯形法相对应的还有对偶单纯形法，二者的算法流程图对比如下所示： 4. 无约束最优化方法 4.1 最优性条件 一阶必要条件：如果 为局部最小点， 则 为驻点，即该点梯度为 。 x1 = 5, x2 = 25, x4 = 5 x ∗ x ∗ 0