
1.前言 ·本课程由数学系开设,旨在讲述求解数学问题的各种最优化方法。 ·本博客仅对课程中的如下内容进详细介绍: 。凸集、凸函数、凸规划 。线性提划际准无式 ·单纯形法 。无约束最优化方法 ·最优性条件 ·最速下降法 ·牛顿法 。约束最优化方法 ·Kuhn-Tucker条件 ·罚函数法 ·闸函数法 2.凸集、凸函数、凸规划 2.1凸集 ·凸焦的定义: 。设SSR",若xD,x∈S,入∈0,1,必有.x+(1-)x2四∈S,则称S为凸集. ·形式化理解凸集的定义,即集合中任意两点连线上的点都在集合内. ·对于凸集的证明,往往利用定义进行证明。 2.2凸函数 ·凸函数的定义 。设集合ScR为凸集,函数f:S一R若x0x2ES.1∈(0.1),恒有 f(x+(1-2)x2≤f(x+(1-)f(x2,则麻f为凸集S上的凸函数 。如果上面不等式以严格不等式成立,则称(x)为凸集S上的严格凸函数 。二阶征 ·f在$上凸,等价于,S中任意一点,其对应的海塞矩阵半正定。 ·f在$上严格凸,等价于,S中任意一点,其对应的海塞矩阵正定, ·凸函数是定义在凸集上的函数,如果要证明凸函数,首先要说明定义域为凸集 2.3凸规划 ·凸规划的定义: 。如果问题(S)中,S为凸集,为凸函数,则称这个问题是凸规划 ·凸规划的定理: 。在凸规划问题中,局部最优解也是全局最优解。 。如果为严格凸函数,则该局部最优解是唯一全局最优解
1. 前言 本课程由数学系开设,旨在讲述求解数学问题的各种最优化方法。 本博客仅对课程中的如下内容进行详细介绍: 凸集、凸函数、凸规划 线性规划 线性规划标准形式 单纯形法 无约束最优化方法 最优性条件 最速下降法 牛顿法 约束最优化方法 Kuhn-Tucker 条件 罚函数法 闸函数法 2. 凸集、凸函数、凸规划 2.1 凸集 凸集的定义: 设 ,若 ,必有 ,则称 为凸集。 形式化理解凸集的定义,即集合中任意两点连线上的点都在集合内。 对于凸集的证明,往往利用定义进行证明。 2.2 凸函数 凸函数的定义: 设集合 为凸集,函数 。若 ,恒有 ,则称 为凸集 上的凸函数。 如果上面不等式以严格不等式成立,则称 为凸集 上的严格凸函数。 凸函数的证明: 凸函数与一阶特征、二阶特征互为充要条件,往往利用二阶特征进行证明, 二阶特征: 在 上凸,等价于, 中任意一点,其对应的海塞矩阵半正定。 在 上严格凸,等价于, 中任意一点,其对应的海塞矩阵正定。 凸函数是定义在凸集上的函数,如果要证明凸函数,首先要说明定义域为凸集。 2.3 凸规划 凸规划的定义: 如果问题 中, 为凸集, 为凸函数,则称这个问题是凸规划。 凸规划的定理: 在凸规划问题中,局部最优解也是全局最优解。 如果 为严格凸函数,则该局部最优解是唯一全局最优解。 S ⊆ R n ∀x (1) , x (2) ∈ S, λ ∈ [0, 1] λx (1) + (1 − λ)x (2) ∈ S S S ⊆ R n f : S → R ∀x (1) , x (2) ∈ S, λ ∈ (0, 1) f (x (1) + (1 − λ)x (2) ) ≤ λf (x (1) ) + (1 − λ)f (x (2) ) f S f(x) S f S S f S S (fS) S f f

·依据凸规划的定理,正明一一个局部最优点为唯一全局最优解,只需证明函数为严格凸函数. ·凸规划的性质十分利于我们寻找问题的最优解,因此我们经常需要证明一个问题是凸规划问题。 3.线性规划 3.1线性规划标准形式 ·首先介绍线性规划的标准形式,之后的单纯形法都是在标准形式上进行计算,对于不是标准形式的线性规划需要对其进行转换 ,标准形式如下 I maxz=cTx (LP)s.t Ax-b X≥0 ·四个特点 。目标最大化 。约束为等式 。决策变量非负 。右端项非负 。约束不是等式的问题:引入松弛变量 。变量无符号限制的问题:用两个非负变量之差来表示一个无符号限制的变量 。右端项有负值的问题:乘以- 3.2单纯形法 ·型行桃是以同布的个级点发,者可方黄的这移男-个相版点要球 单纯形法的计算比较简单,这里只给出例子进行说明。 maxz=1500x1+2500x2 3x1+2X2+X3=65 (LP) 2x1+x2+x4=40 3x2+X5=75 X1,X2,X3,X4,X520
依据凸规划的定理,证明一个局部最优点为唯一全局最优解,只需证明函数 为严格凸函数。 凸规划的性质十分利于我们寻找问题的最优解,因此我们经常需要证明一个问题是凸规划问题。 3. 线性规划 3.1 线性规划标准形式 首先介绍线性规划的标准形式,之后的单纯形法都是在标准形式上进行计算,对于不是标准形式的线性规划需要对其进行转换。 标准形式如下: 四个特点: 目标最大化 约束为等式 决策变量非负 右端项非负 采用如下方式,将一般形式转化为标准化形式: 极小化目标函数的问题:利用负号转化为目标最大化 约束不是等式的问题:引入松弛变量 变量无符号限制的问题:用两个非负变量之差来表示一个无符号限制的变量 右端项有负值的问题:乘以 3.2 单纯形法 单纯形法的基本思路是有选择地取基本可行解,即是从可行域的一个极点出发,沿着可行域的边界移到另一个相邻的极点,要求 新极点的目标函数值不比原目标函数值差。 单纯形法要求系数矩阵中存在单位阵,将其作为初始的基本可行解,之后一步步迭代。对于某些标准形式中不含有单位阵的线性 规划问题,可以采用大M法和两阶段法。 单纯形法的计算比较简单,这里只给出例子进行说明。 f (LP) ⎧⎪ ⎨ ⎪⎩ max z = c T x s. t. Ax = b x ≥ 0 −1 (LP) ⎧⎪⎪⎪⎪⎪⎪ ⎨ ⎪⎪⎪⎪⎪⎪⎩ max z = 1500x1 + 2500x2 3x1 + 2x2 + x3 = 65 2x1 + x2 + x4 = 40 3x2 + x5 = 75 x1 , x2 , x3 , x4 , x5 ≥ 0
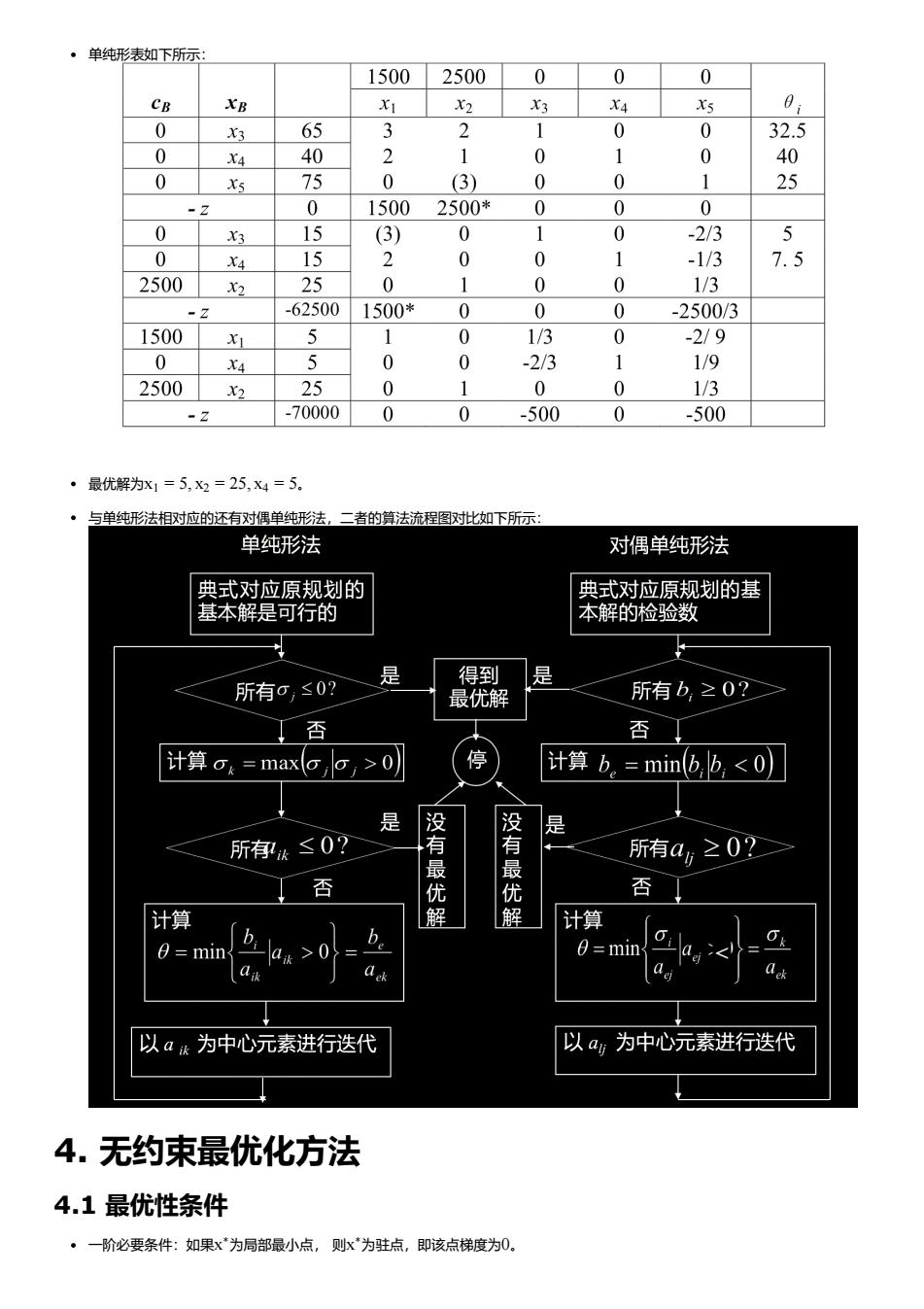
·单纯形表如下所示 1500 2500 0 0 0 CR XR Xs 65 0 40 32 0 0 32.5 0 40 0 75 0 (3) 0 0 25 0 1500 2500* 0 0 X3 15 (3) 0 -2/3 5 0 X4 15 0 -1/3 7.5 2500 25 0 1/3 -625001500* 0 0 0 -2500/3 1500 5 0 1/3 0 -2/9 0 0 0 -23 1 4 1/9 2500x2 25 0 0 0 1/3 -z -700000 0 -500 0 -500 ·最优解为x1=5,X2=25,x4=5 与单纯形法相对应的还有对偶单纯形法 二者的算法流程图对比如下所示 单纯形法 对偶单纯形法 典式对应原规划的 典式对应原规划的基 基本解是可行的 本解的检验数 所有0,≤0? 、是 得到是 最优解 0) 停 计算b.=minb,b, 优 计算 解 计算 0=min b b a> a 以a法为中心元素进行迭代 以a为中心元素进行迭代 4.无约束最优化方法 4.1最优性条件 ·一阶必要条件:如果x为局部最小点,则x为驻点,即该点梯度为0
单纯形表如下所示: 最优解为 。 与单纯形法相对应的还有对偶单纯形法,二者的算法流程图对比如下所示: 4. 无约束最优化方法 4.1 最优性条件 一阶必要条件:如果 为局部最小点, 则 为驻点,即该点梯度为 。 x1 = 5, x2 = 25, x4 = 5 x ∗ x ∗ 0
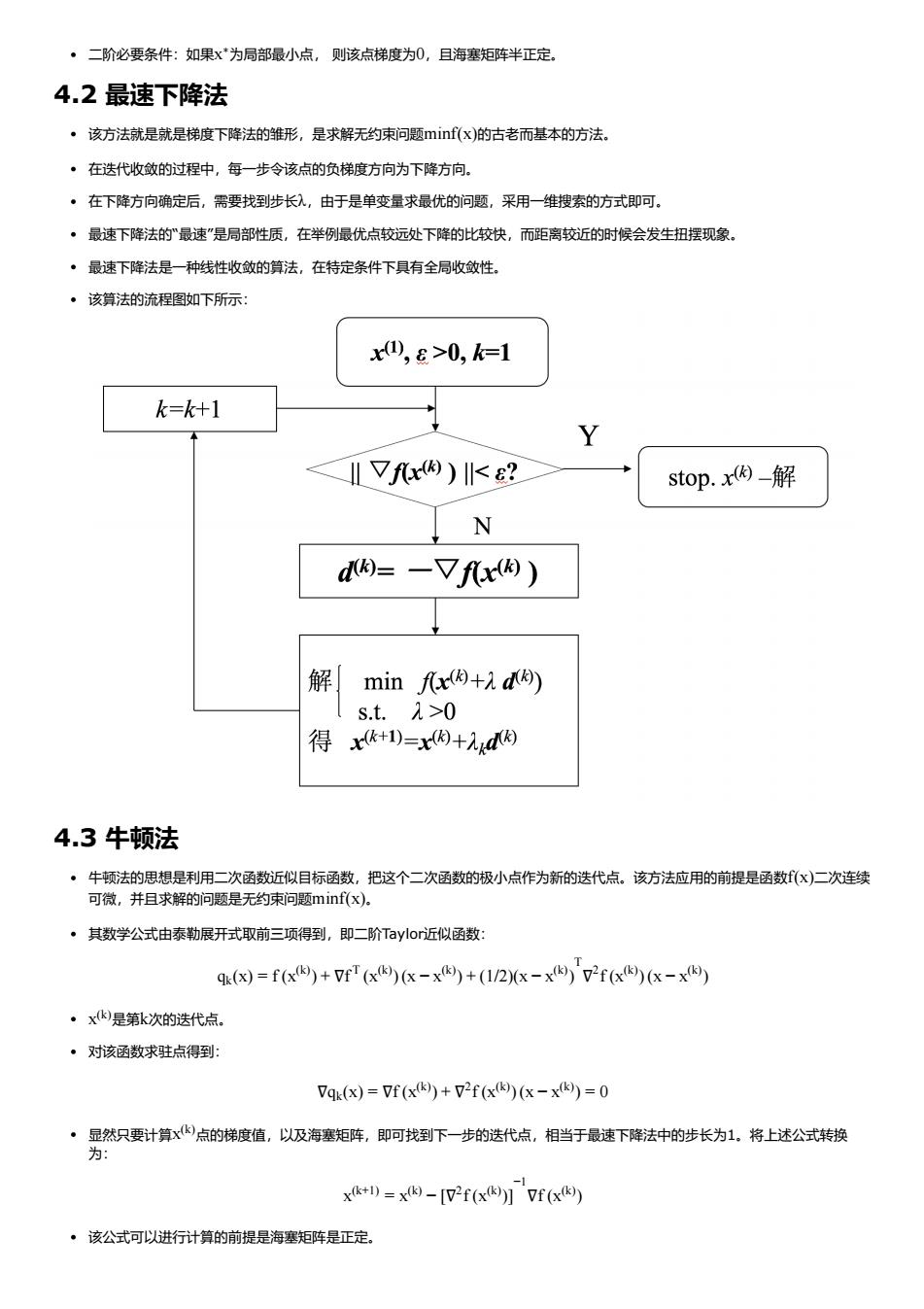
·二阶必要条件:如果×为局部最小点,则该点梯度为0,且海塞矩阵半正定, 4.2最速下降法 ·该方法就是就是梯度下降法的雏形,是求解无约束问题mi(x)的古者而基本的方法。 ·在法代收敛的过程中,每一步令该点的负梯度方向为下降方向。 ·在下降方向确定后,需要找到步长入,由于是单变量求最优的问题,采用一维搜索的方式即可。 ·最速下降法的”最速"是局部性质,在举例最优点较远处下降的比较快,而距离较近的时候会发生扭摆现象 ·最速下降法是一种线性收敛的慎法,在特定条件下具有全局收敛性。 ·该算法的流程图如下所示: x四,&>0,k=1 k=k+1 Vfx())0 得I)=x因+d因 4.3牛顿法 ·牛顿法的思想是利用二次函数近似目标函数,把这个二次函数的极小点作为新的达代点。该方法应用的前提是函数(x)二次连续 可微,并目求解的问题是无约束问题minf(x). ·其数学公式由泰勒展开式取前三项得到,即二阶Tayo近似函数: 9()=f(x)+F'(6x)K-x+(12x-x)72f(x(x-x ·xk是第k次的迭代点。 ·对该涵数求驻点得到 7q.(x)=7f(x+72f(x(x-x=0 ‘男只麦情株室道吸海定库,阿浅下少的选代点相酯于连降去中的长为1.将上送公装 xk+)=x-2fy7f6 ·该公式可以进行计算的前提是海塞矩阵是正定
二阶必要条件:如果 为局部最小点, 则该点梯度为 ,且海塞矩阵半正定。 4.2 最速下降法 该方法就是就是梯度下降法的雏形,是求解无约束问题 的古老而基本的方法。 在迭代收敛的过程中,每一步令该点的负梯度方向为下降方向。 在下降方向确定后,需要找到步长 ,由于是单变量求最优的问题,采用一维搜索的方式即可。 最速下降法的“最速”是局部性质,在举例最优点较远处下降的比较快,而距离较近的时候会发生扭摆现象。 最速下降法是一种线性收敛的算法,在特定条件下具有全局收敛性。 该算法的流程图如下所示: 4.3 牛顿法 牛顿法的思想是利用二次函数近似目标函数,把这个二次函数的极小点作为新的迭代点。该方法应用的前提是函数 二次连续 可微,并且求解的问题是无约束问题 。 其数学公式由泰勒展开式取前三项得到,即二阶Taylor近似函数: 是第 次的迭代点。 对该函数求驻点得到: 显然只要计算 点的梯度值,以及海塞矩阵,即可找到下一步的迭代点,相当于最速下降法中的步长为1。将上述公式转换 为: 该公式可以进行计算的前提是海塞矩阵是正定。 x ∗ 0 minf(x) λ f(x) minf(x) qk(x) = f (x (k) ) + ∇f T (x (k) ) (x − x (k) ) + (1/2)(x − x (k) ) T ∇ 2 f (x (k) ) (x − x (k) ) x (k) k ∇qk(x) = ∇f (x (k) ) + ∇ 2 f (x (k) ) (x − x (k) ) = 0 x (k) x (k+1) = x (k) − [∇ 2 f (x (k) )] −1 ∇f (x (k) )

·牛顿法的慎法流程图如下所示: x,0,k=1 实用中,判断 k=k+1 若72f例非正定时 进行相应处理 (k))S=-vfx(h) 得s因,xk+)=x)+s因 N Is网IKe2 STOP:x)-L.opt. ·牛本的收效速宝为二价。于平方改效。牛锈法对正定二次通数步这代即可达到最优器,因此具有二次终结生 。牛顿法的缺点 。牛顿法是局部收敛的,在初始点选择不当时,往往导致不收敛。 。牛顿法不是下降算法,当二阶海塞矩阵非正定时,不能保证产生的方向是下降方向。 。二阶海塞矩阵必须可逆。 。要求函数二阶连续可微,计算量大, 5.约束最优化方法 ·约束最优化问题是实践中常见的问题,难度大于无约束最优化问题.约束最优化问题的形式一般是(fgh)问题,即: I minf(x) (fgh)s.tgx)≤0 h(x)=0 5.1Kuhn-Tucker条件 ·对于(gh)问题,K-T条件的公式如下: +名e+y7%们-0 e1 ·要求所有的u值非负。 ·通过对上述公式求解,便找到了满足K-T条件的K-T点 ·在约束最优化问题中,K-T条件相当于无约束最优化问题中的驻点条件,即寻找到KT点便找到了问题的局部最优解, 。有些问题需要说明K-T点是全局最优解,只需要证明问题是凸规划即可,详见2.3京节的介绍 5.2罚函数法(外点法) ·解决玉树问题的一个直接想法是,把违背约束作为对求最小值的一种惩罚,把约束加入到目标函数,从而得到了一个辅助的无约 型本不思想 ·构造的辅助函数形式如下: minf(x)+μa(x) ·为罚因子,大于0
牛顿法的算法流程图如下所示: 牛顿法的优点 牛顿法的收敛速度为二阶,属于平方收敛。牛顿法对正定二次函数一步迭代即可达到最优解,因此具有二次终结性。 牛顿法的缺点 牛顿法是局部收敛的,在初始点选择不当时,往往导致不收敛。 牛顿法不是下降算法,当二阶海塞矩阵非正定时,不能保证产生的方向是下降方向。 二阶海塞矩阵必须可逆。 要求函数二阶连续可微,计算量大。 5. 约束最优化方法 约束最优化问题是实践中常见的问题,难度大于无约束最优化问题。约束最优化问题的形式一般是 问题,即: 5.1 Kuhn-Tucker条件 对于 问题,K-T条件的公式如下: 要求所有的 值非负。 通过对上述公式求解,便找到了满足K-T条件的K-T点。 在约束最优化问题中,K-T条件相当于无约束最优化问题中的驻点条件,即寻找到K-T点便找到了问题的局部最优解。 有些问题需要说明K-T点是全局最优解,只需要证明问题是凸规划即可,详见2.3章节的介绍。 5.2 罚函数法(外点法) 解决玉树问题的一个直接想法是,把违背约束作为对求最小值的一种惩罚,把约束加入到目标函数,从而得到了一个辅助的无约 束最优化问题,之后采用无约束最优化方法进行求解,这就是罚函数的基本思想。 在实际求解无约束最优化问题时,求驻点便可以解决大多数问题。 构造的辅助函数形式如下: 为罚因子,大于0。 (fgh) (fgh) ⎧⎪ ⎨ ⎪⎩ min f(x) s. t. g(x) ≤ 0 h(x) = 0 (fgh) ∇f (x ∗ ) + ∑ i∈I u ∗ i ∇gi (x ∗ ) + l ∑ j=1 v ∗ j ∇hj (x ∗ ) = 0 u minf(x) + μα(x) μ

·其钟a(x)=∑m1中(g(x》+∑1ph(x) ·通常令(x)=max0,xP,p(x)=NP,p值通常为2. ·求解过程就是对辅助函数求驻点,并计算u趋近无穷大时,最优解的值 5.3闸函数法(内点法) ·闸函数适用于不等式约束问题,即(g)问题。思想与罚函数基本相同。不同点在于该方法将惩罚家在约束集的边界,当靠近边界 时,惩罚项无穷大。 ·构造的辅助函数形式如下: minf(x)+uB(x) ·μ为罚因子,大于0。 ·其钟B(x)=∑(g(x) ·通常令x)=- ·求解过程就是对埔助函数求驻点,并计算μ趋近0广时,最优解的值
其中 通常令 , , 值通常为 。 求解过程就是对辅助函数求驻点,并计算 趋近无穷大时,最优解的值。 5.3 闸函数法(内点法) 闸函数适用于不等式约束问题,即 问题。思想与罚函数基本相同。不同点在于该方法将惩罚家在约束集的边界,当靠近边界 时,惩罚项无穷大。 构造的辅助函数形式如下: 为罚因子,大于0。 其中 通常令 。 求解过程就是对辅助函数求驻点,并计算 趋近 时,最优解的值。 α(x) = ∑ m i=1 ϕ (gi(x)) + ∑ 1 j=1 φ (hj(x)) ϕ(x) = [max0, x] p φ(x) = |x| p p 2 μ (fg) minf(x) + μB(x) μ B(x) = ∑ m i=1 ϕ (gi(x)) ϕ(x) = − 1 x μ 0 +