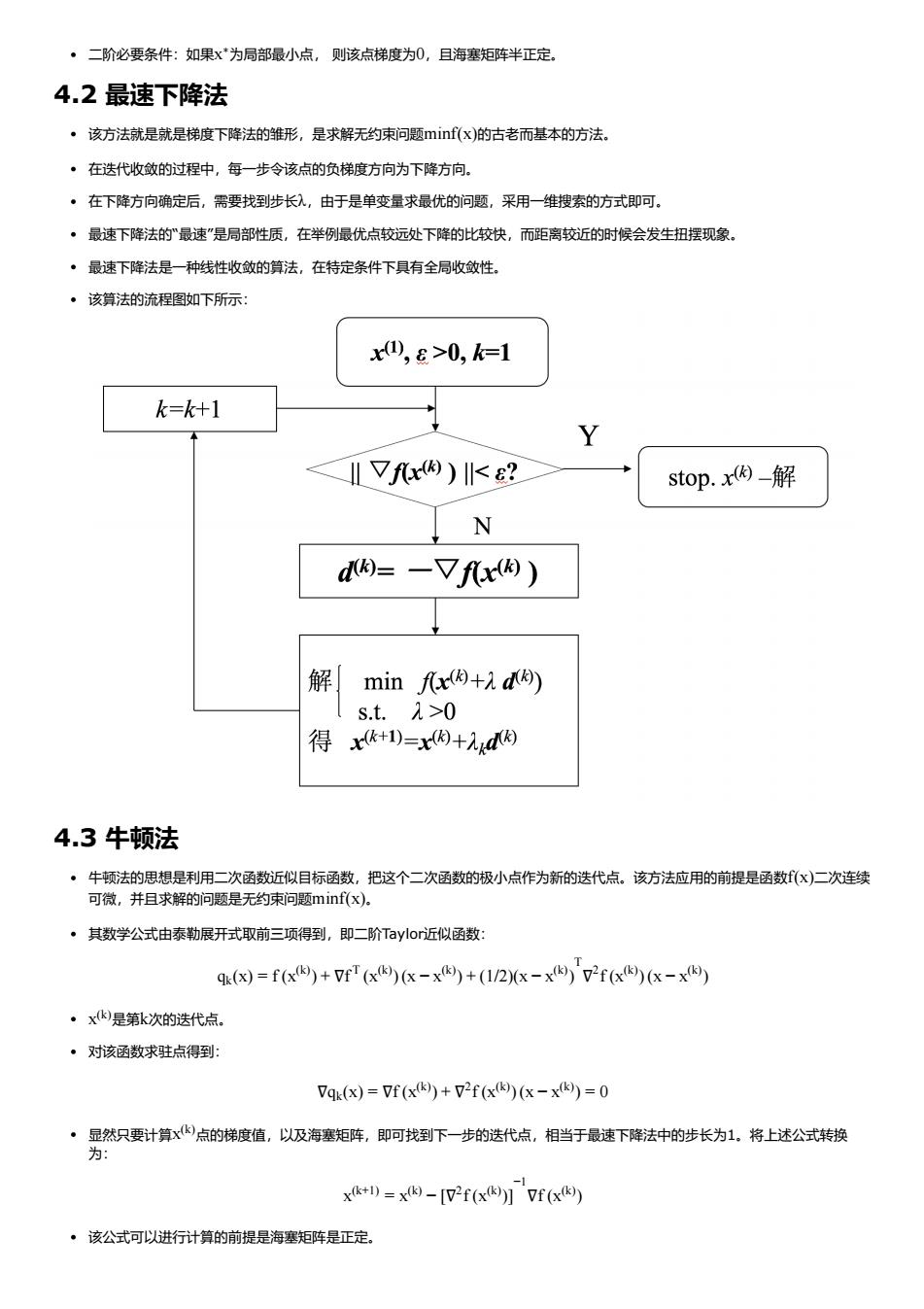
·二阶必要条件：如果×为局部最小点，则该点梯度为0，且海塞矩阵半正定， 4.2最速下降法 ·该方法就是就是梯度下降法的雏形，是求解无约束问题mi(x)的古者而基本的方法。 ·在法代收敛的过程中，每一步令该点的负梯度方向为下降方向。 ·在下降方向确定后，需要找到步长入，由于是单变量求最优的问题，采用一维搜索的方式即可。 ·最速下降法的”最速"是局部性质，在举例最优点较远处下降的比较快，而距离较近的时候会发生扭摆现象 ·最速下降法是一种线性收敛的慎法，在特定条件下具有全局收敛性。 ·该算法的流程图如下所示： x四，&>0，k=1 k=k+1 Vfx())<E? stop.x因_解 N d=一Vfx因) 解min因+d) 1s.t.1>0 得I)=x因+d因 4.3牛顿法 ·牛顿法的思想是利用二次函数近似目标函数，把这个二次函数的极小点作为新的达代点。该方法应用的前提是函数(x)二次连续 可微，并目求解的问题是无约束问题minf(x). ·其数学公式由泰勒展开式取前三项得到，即二阶Tayo近似函数： 9()=f(x)+F'(6x)K-x+(12x-x)72f(x(x-x ·xk是第k次的迭代点。 ·对该涵数求驻点得到 7q.(x)=7f(x+72f(x(x-x=0 ‘男只麦情株室道吸海定库，阿浅下少的选代点相酯于连降去中的长为1.将上送公装 xk+)=x-2fy7f6 ·该公式可以进行计算的前提是海塞矩阵是正定。二阶必要条件：如果 为局部最小点， 则该点梯度为 ，且海塞矩阵半正定。 4.2 最速下降法 该方法就是就是梯度下降法的雏形，是求解无约束问题 的古老而基本的方法。 在迭代收敛的过程中，每一步令该点的负梯度方向为下降方向。 在下降方向确定后，需要找到步长 ，由于是单变量求最优的问题，采用一维搜索的方式即可。 最速下降法的“最速”是局部性质，在举例最优点较远处下降的比较快，而距离较近的时候会发生扭摆现象。 最速下降法是一种线性收敛的算法，在特定条件下具有全局收敛性。 该算法的流程图如下所示： 4.3 牛顿法 牛顿法的思想是利用二次函数近似目标函数，把这个二次函数的极小点作为新的迭代点。该方法应用的前提是函数 二次连续 可微，并且求解的问题是无约束问题 。 其数学公式由泰勒展开式取前三项得到，即二阶Taylor近似函数： 是第 次的迭代点。 对该函数求驻点得到： 显然只要计算 点的梯度值，以及海塞矩阵，即可找到下一步的迭代点，相当于最速下降法中的步长为1。将上述公式转换 为： 该公式可以进行计算的前提是海塞矩阵是正定。 x ∗ 0 minf(x) λ f(x) minf(x) qk(x) = f (x (k) ) + ∇f T (x (k) ) (x − x (k) ) + (1/2)(x − x (k) ) T ∇ 2 f (x (k) ) (x − x (k) ) x (k) k ∇qk(x) = ∇f (x (k) ) + ∇ 2 f (x (k) ) (x − x (k) ) = 0 x (k) x (k+1) = x (k) − [∇ 2 f (x (k) )] −1 ∇f (x (k) )