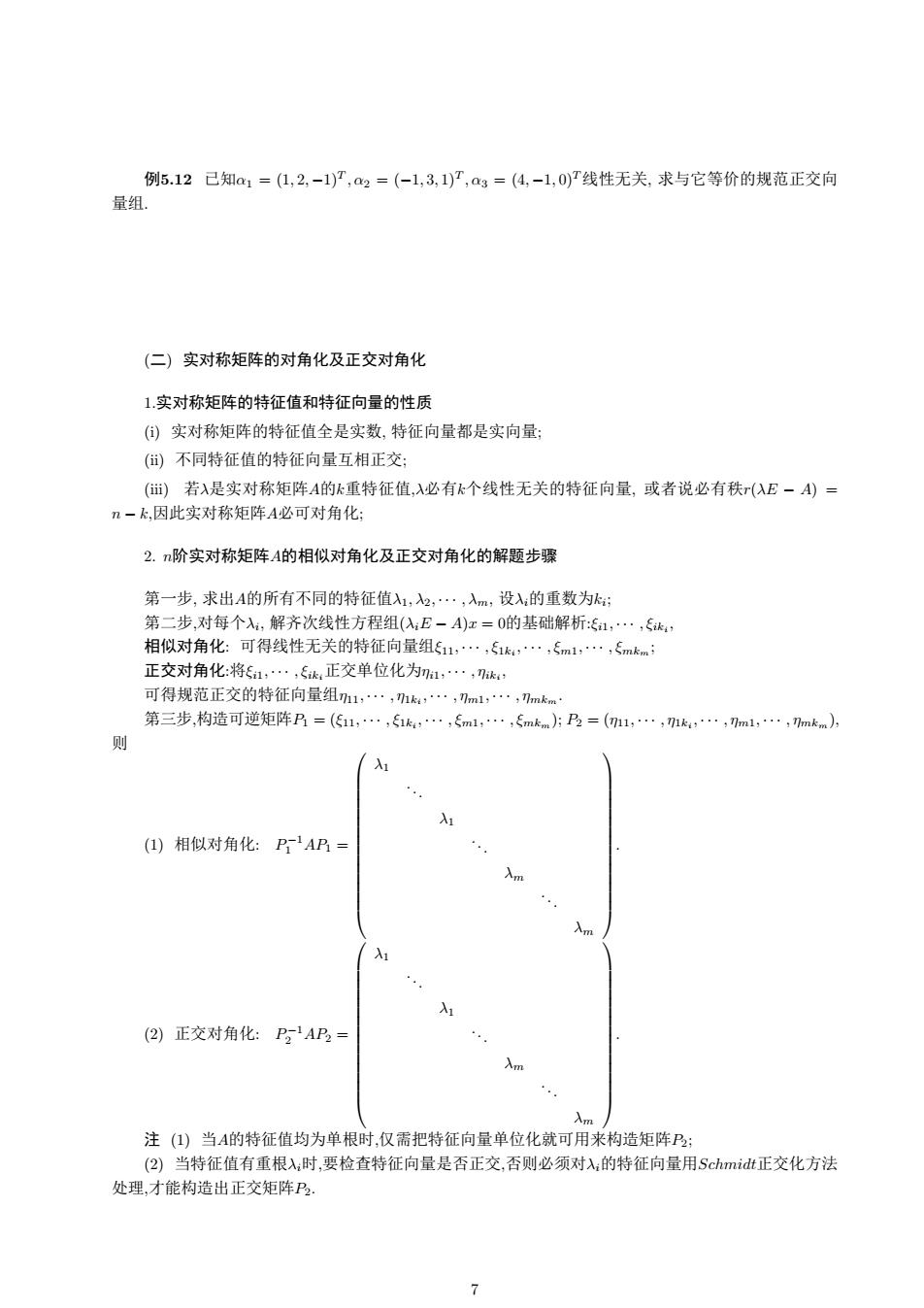
例5.12已知@1=(1,2，-1)7，a2=(-1,3,1)T,a4=(4,-1,0T线性无关，求与它等价的规范正交向 量组 (仁)实对称矩阵的对角化及正交对角化 1,实对称矩阵的特征值和特征向量的性质 (句)实对称矩阵的特征值全是实数，特征向量都是实向量： ()不同特征值的特征向量互相正交： ()若入是实对称矩阵A的k重特征值，A必有k个线性无关的特征向量，或者说必有秩(AE一A)= 2一k因此实对称矩阵A必可对角化： 2.n阶实对称矩阵A的相似对角化及正交对角化的解题步骤 第一步，求出A的所有不同的特征值入1，λ2，·，，入m,设入的重数为k: 第二步，对每个X,解齐次线性方程组(0E-A)z=0的基础解析：1，·， 相似对角化：可得线性无关的特征向量组11，…，1k,…,m1,…,5mk 正衣时鱼化将 ,正交单位化为m… ,k 可得规范正交的特征向量组1，…，mk,·,m,,mk. 第三步，构造可逆矩阵乃=（低11，…，1k,…,ml,…,mkm)方乃=(11，…，mk…,ml,…,mkm) 则 入1 (①)相似对角化：PAP 入 (②)正交对角化：A乃 注()当A的特征值均为单根时，仅需把特征向量单位化就可用来构造矩阵B; (②)当特征值有重根入，时，要检查特征向量是否正交，否则必须对的特征向量用Schmidt正交化方法 处理，才能构造出正交矩阵B 7~5.12 Æα1 = (1, 2, −1)T , α2 = (−1, 3, 1)T , α3 = (4, −1, 0)TÇ5Ã', ¶Üßd5âï ˛|. () ¢È°› Èz9Èz 1.¢È°› Aä⁄Aï˛5ü (i) ¢È°› A䥢Í, Aï˛—¥¢ï˛; (ii) ÿ”AäAï˛pÉ; (iii) eλ¥¢È°› Ak­Aä,λ7kkáÇ5Ã'Aï˛, ½ˆ`7kùr(λE − A) = n − k,œd¢È°› A7åÈz; 2. n¢È°› AÉqÈz9Èz)K⁄½ 1ò⁄, ¶—A§kÿ”Aäλ1, λ2, · · · , λm, λi­Íèki ; 1⁄,Èzáλi , )‡gÇ5êß|(λiE − A)x = 0ƒ:)¤:ξi1, · · · , ξiki , ÉqÈz: åÇ5Ã'Aï˛|ξ11, · · · , ξ1ki , · · · , ξm1, · · · , ξmkm; Èz:Úξi1, · · · , ξiki¸†zèηi1, · · · , ηiki , å5âAï˛|η11, · · · , η1ki , · · · , ηm1, · · · , ηmkm. 1n⁄,Eå_› P1 = (ξ11, · · · , ξ1ki , · · · , ξm1, · · · , ξmkm); P2 = (η11, · · · , η1ki , · · · , ηm1, · · · , ηmkm), K (1) ÉqÈz: P −1 1 AP1 =   λ1 . . . λ1 . . . λm . . . λm   . (2) Èz: P −1 2 AP2 =   λ1 . . . λ1 . . . λm . . . λm   . 5 (1) AAä˛è¸äû,=IrAï˛¸†z“å^5E› P2; (2) Aäk­äλiû,áuAï˛¥ƒ,ƒK7LÈλiAï˛^Schmidtzê{ ?n,‚UE—› P2. 7