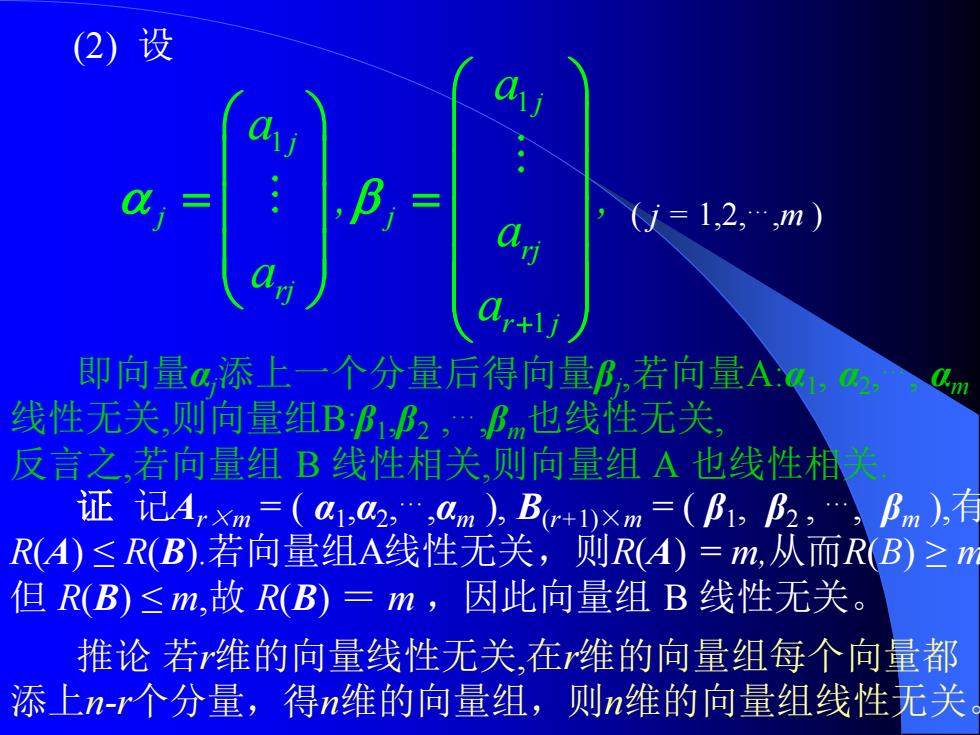
(2)设 ?i=1,2,…,m） r+1 即向量a添上一个分量后得向量B,若向量Ag1,, 线性无关，则向量组B邛1B2,B也线性无关 反言之，若向量组B线性相关，则向量组A也线性相关 证记ArXm=(a1,a2,am）,B+1)Xm=(f,B2,fm),看 RA)≤R(B).若向量组A线性无关，则RA)=m,从而R(B)≥n 但R(B)≤m,故R(B)=m,因此向量组B线性无关。 推论若维的向量线性无关，在维的向量组每个向量都 添上n-r个分量，得n维的向量组，则n维的向量组线性无关 (2) 设 1 1 1   +           = =               j j j j rj rj r j a a , , a a a ( j = 1,2,…,m ) 即向量αj添上一个分量后得向量βj ,若向量A:α1 , α2 ,…, αm 线性无关,则向量组B:β1 ,β2 ,…,βm也线性无关, 反言之,若向量组 B 线性相关,则向量组 A 也线性相关. 证 记Ar×m = ( α1 ,α2 ,…,αm ), B(r+1)×m = ( β1 , β2 , …, βm ),有 R(A) ≤ R(B).若向量组A线性无关，则R(A) = m,从而R(B) ≥ m. 但 R(B) ≤ m,故 R(B) ＝ m ，因此向量组 B 线性无关。 推论 若r维的向量线性无关,在r维的向量组每个向量都 添上n-r个分量，得n维的向量组，则n维的向量组线性无关