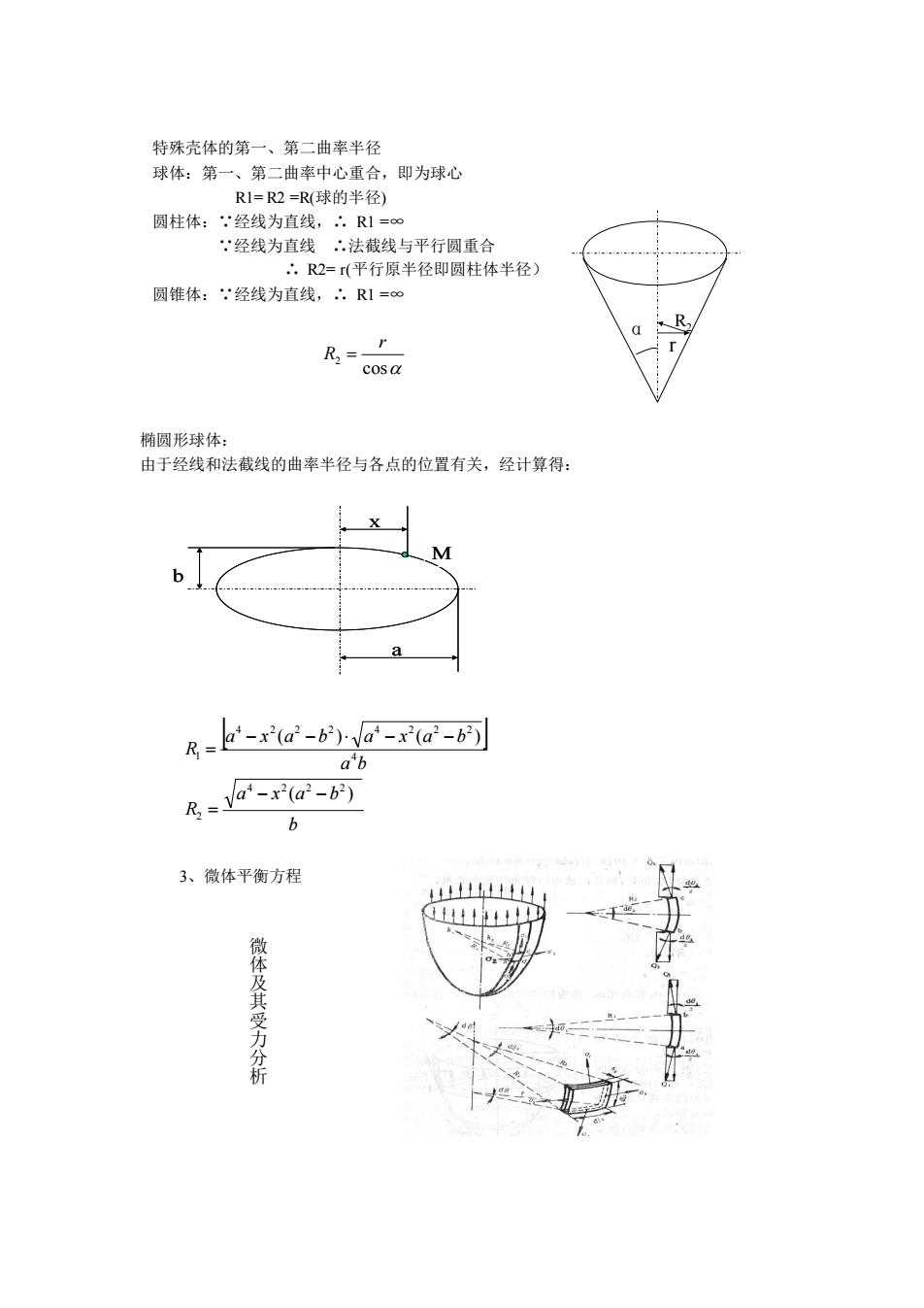
椭圆形球体： 由于经线和法截线的曲率半径与各点的位置有关，经计算得： 3、微体平衡方程 微 体 及 其 受 力 分 析 特殊壳体的第一、第二曲率半径 球体：第一、第二曲率中心重合，即为球心 R1= R2 =R(球的半径) 圆柱体：∵经线为直线，∴ R1 =∞ ∵经线为直线 ∴法截线与平行圆重合 ∴ R2= r(平行原半径即圆柱体半径） 圆锥体：∵经线为直线，∴ R1 =∞ cos 2 r R = R2 r α   b a x a b R a b a x a b a x a b R ( ) ( ) ( ) 4 2 2 2 2 4 4 2 2 2 4 2 2 2 1 − − = − −  − − = a x b M椭圆形球体： 由于经线和法截线的曲率半径与各点的位置有关，经计算得： 3、微体平衡方程 微 体 及 其 受 力 分 析 特殊壳体的第一、第二曲率半径 球体：第一、第二曲率中心重合，即为球心 R1= R2 =R(球的半径) 圆柱体：∵经线为直线，∴ R1 =∞ ∵经线为直线 ∴法截线与平行圆重合 ∴ R2= r(平行原半径即圆柱体半径） 圆锥体：∵经线为直线，∴ R1 =∞ cos 2 r R = R2 r α   b a x a b R a b a x a b a x a b R ( ) ( ) ( ) 4 2 2 2 2 4 4 2 2 2 4 2 2 2 1 − − = − −  − − = a x b M