哈尔滨商业大学：《食品机械》课程教学资源（教案讲义）第五章 容器设计 5.2 第二节 旋转壳体的受力分析

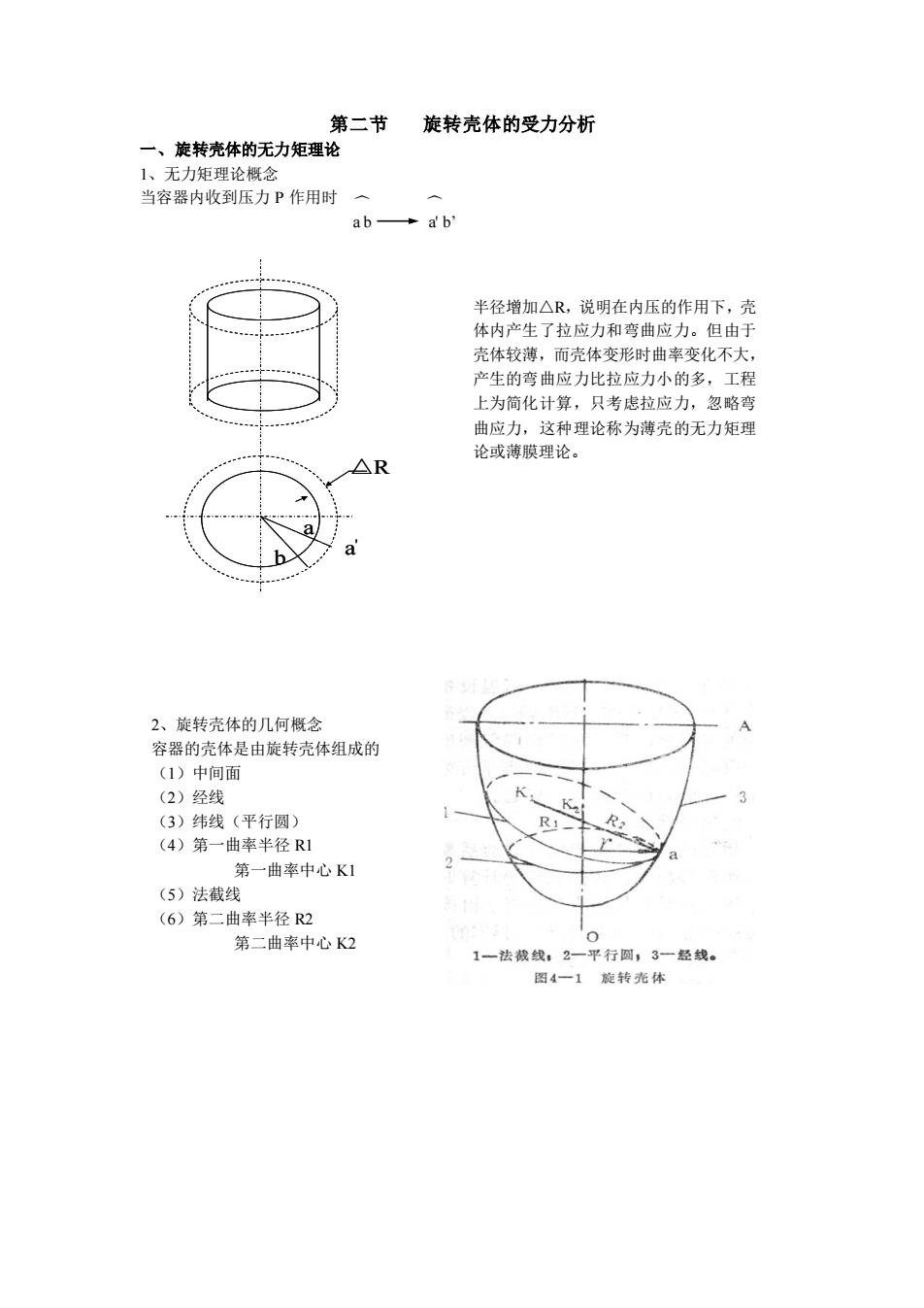
第二节 旋转壳体的受力分析 一、旋转壳体的无力矩理论 1、无力矩理论概念 当容器内收到压力 P 作用时 ︿ ︿ a b a' b’ 半径增加△R，说明在内压的作用下，壳 体内产生了拉应力和弯曲应力。但由于 壳体较薄，而壳体变形时曲率变化不大， 产生的弯曲应力比拉应力小的多，工程 上为简化计算，只考虑拉应力，忽略弯 曲应力，这种理论称为薄壳的无力矩理 论或薄膜理论。 △R a b a ' △R a b a ' 2、旋转壳体的几何概念 容器的壳体是由旋转壳体组成的 （1）中间面 （2）经线 （3）纬线（平行圆） （4）第一曲率半径 R1 第一曲率中心 K1 （5）法截线 （6）第二曲率半径 R2 第二曲率中心 K2

第二节 旋转壳体的受力分析 一、旋转壳体的无力矩理论 1、无力矩理论概念 当容器内收到压力 P 作用时 ︿ ︿ a b a' b’ 半径增加△R，说明在内压的作用下，壳 体内产生了拉应力和弯曲应力。但由于 壳体较薄，而壳体变形时曲率变化不大， 产生的弯曲应力比拉应力小的多，工程 上为简化计算，只考虑拉应力，忽略弯 曲应力，这种理论称为薄壳的无力矩理 论或薄膜理论。 △R a b a ' △R a b a ' 2、旋转壳体的几何概念 容器的壳体是由旋转壳体组成的 （1）中间面 （2）经线 （3）纬线（平行圆） （4）第一曲率半径 R1 第一曲率中心 K1 （5）法截线 （6）第二曲率半径 R2 第二曲率中心 K2

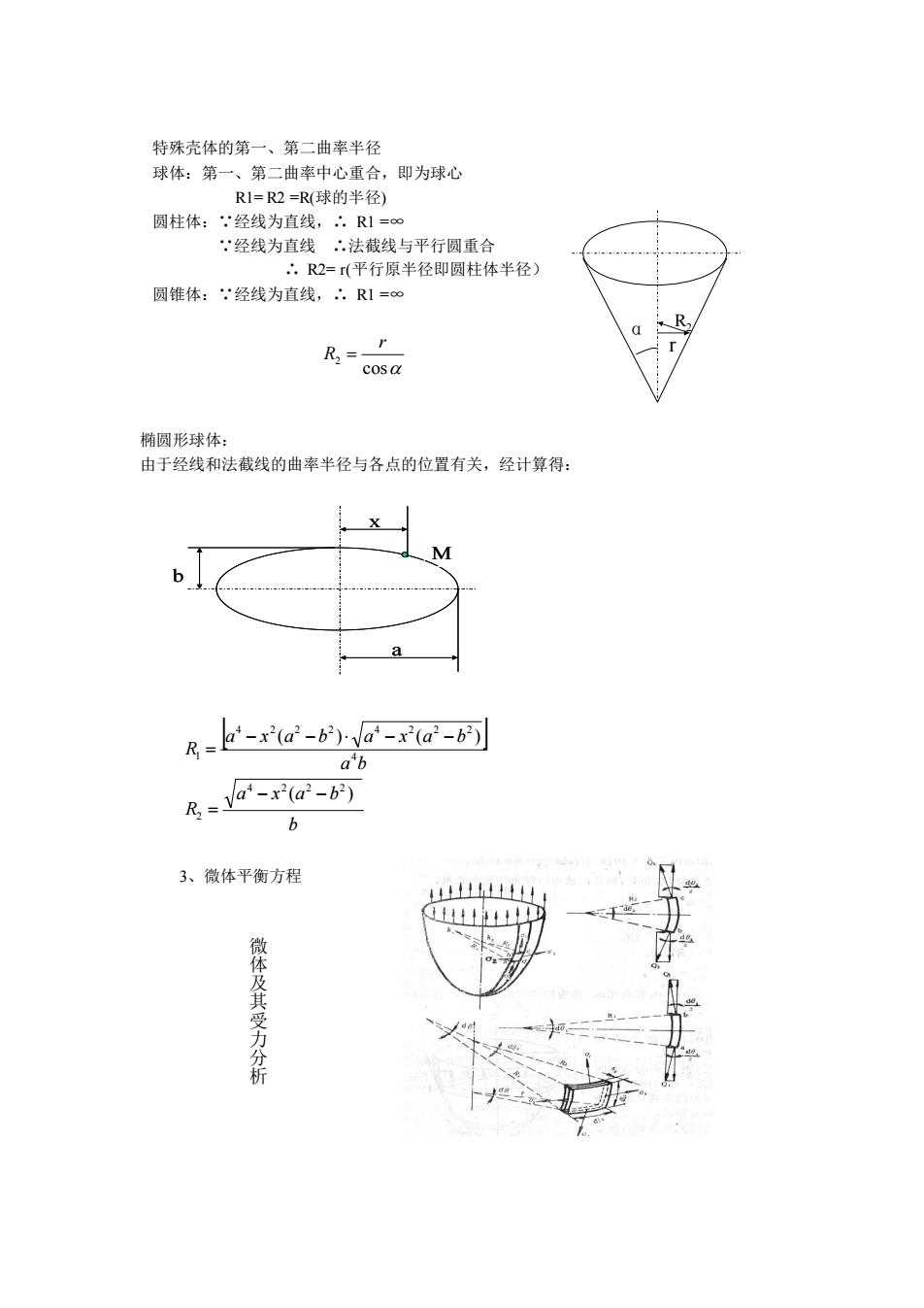
椭圆形球体： 由于经线和法截线的曲率半径与各点的位置有关，经计算得： 3、微体平衡方程 微 体 及 其 受 力 分 析 特殊壳体的第一、第二曲率半径 球体：第一、第二曲率中心重合，即为球心 R1= R2 =R(球的半径) 圆柱体：∵经线为直线，∴ R1 =∞ ∵经线为直线 ∴法截线与平行圆重合 ∴ R2= r(平行原半径即圆柱体半径） 圆锥体：∵经线为直线，∴ R1 =∞ cos 2 r R = R2 r α   b a x a b R a b a x a b a x a b R ( ) ( ) ( ) 4 2 2 2 2 4 4 2 2 2 4 2 2 2 1 − − = − −  − − = a x b M

椭圆形球体： 由于经线和法截线的曲率半径与各点的位置有关，经计算得： 3、微体平衡方程 微 体 及 其 受 力 分 析 特殊壳体的第一、第二曲率半径 球体：第一、第二曲率中心重合，即为球心 R1= R2 =R(球的半径) 圆柱体：∵经线为直线，∴ R1 =∞ ∵经线为直线 ∴法截线与平行圆重合 ∴ R2= r(平行原半径即圆柱体半径） 圆锥体：∵经线为直线，∴ R1 =∞ cos 2 r R = R2 r α   b a x a b R a b a x a b a x a b R ( ) ( ) ( ) 4 2 2 2 2 4 4 2 2 2 4 2 2 2 1 − − = − −  − − = a x b M

微体上作用的内力和外力见图4一2，图中： 5。—壳体的理论壁厚， 1,一微体沿经线的长度， d12一·体沿法线的长度 R:-一第一曲率半径 R2一一第二曲率半径 d6一一微体上两个第一曲率半径的夹角 d02一微体上两个第二曲率半径的夹角， 1一一经向应力 口2.一环向应力， p 壳体的内压力。 由于内压力的作用，在微体bcd面积（壳体内表面）上所受到的外力。 P=pdl dla 微体四个截面上产生的内力则分别为 bc与ad载面上的径向拉力 Q=dl ab与cd截面上的环向拉力 Q:0:5dl 将微体所受的上述各力，沿微体法线方向投影，得力平衡方程 如5如尊+a如普p 由于微体的曲辛径夹角d0,和d胡，微小故可以作如下近似代换 4量 号是 把它们代入上式，整理后可得： 受量 (-1) 此方程式联系膏膜应力0、：和内压P,称为微体平衡方程式：它由Laplace首先导出， 权称为啦普拉斯方程。

二、无力矩理论的应用

二、无力矩理论的应用

在直径压力相等的情况下，球形壳体的应力只为圆形壳体环向应力的一半，其壁厚也就减 0 0 1 2 2 4S pD S pR  = = = =

在直径压力相等的情况下，球形壳体的应力只为圆形壳体环向应力的一半，其壁厚也就减 0 0 1 2 2 4S pD S pR  = = = =

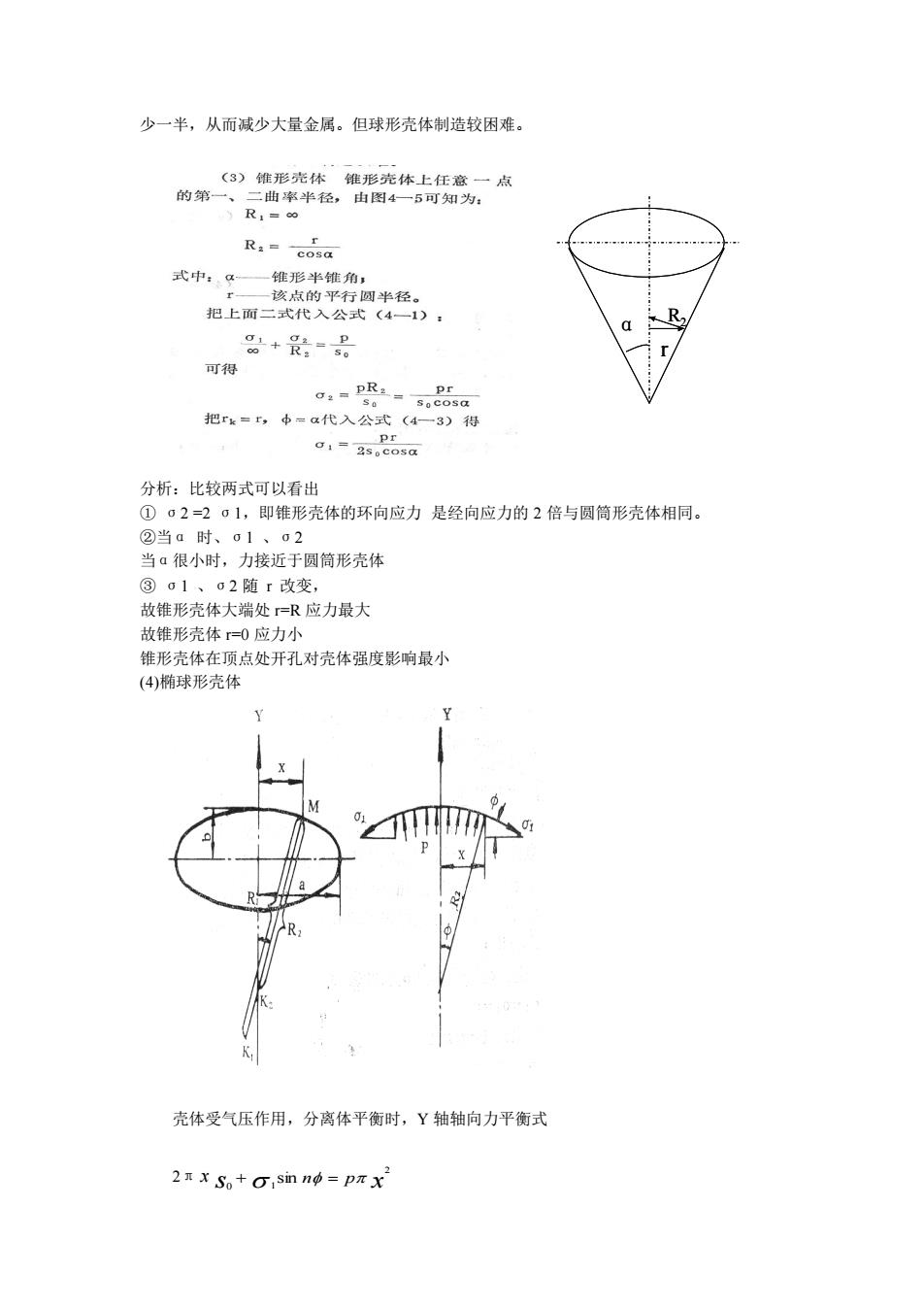
少一半，从而减少大量金属。但球形壳体制造较困难。 分析：比较两式可以看出 ① σ2 =2 σ1，即锥形壳体的环向应力 是经向应力的 2 倍与圆筒形壳体相同。 ②当α 时、σ1 、σ2 当α很小时，力接近于圆筒形壳体 ③ σ1 、σ2 随 r 改变， 故锥形壳体大端处 r=R 应力最大 故锥形壳体 r=0 应力小 锥形壳体在顶点处开孔对壳体强度影响最小 (4)椭球形壳体 壳体受气压作用，分离体平衡时，Y 轴轴向力平衡式 2π x + s0 n p x 2 1  sin  =  R2 r α

少一半，从而减少大量金属。但球形壳体制造较困难。 分析：比较两式可以看出 ① σ2 =2 σ1，即锥形壳体的环向应力 是经向应力的 2 倍与圆筒形壳体相同。 ②当α 时、σ1 、σ2 当α很小时，力接近于圆筒形壳体 ③ σ1 、σ2 随 r 改变， 故锥形壳体大端处 r=R 应力最大 故锥形壳体 r=0 应力小 锥形壳体在顶点处开孔对壳体强度影响最小 (4)椭球形壳体 壳体受气压作用，分离体平衡时，Y 轴轴向力平衡式 2π x + s0 n p x 2 1  sin  =  R2 r α

分析： 经向应力 ①从经向应力计算时可看出， 无论 x 为何值，σ1>0,即σ1 都是拉应力 ②顶点处（x=0、 y=b) 顶点处σ1 有最大值 ③边缘处(x=a, y=0) 0 2 0 2 0 1 2 sin 2 sin 2 sin S pR S pR S px = = =     2 0 2 1 1 S p R R + =   1 2 1 0 2 2 R R S pR  = − 0 2 1 2S pR  = (2 ) 2 1 2 0 2 0 2 1 2 0 2 2 R R S pR S pR R R S pR  = − = − 环向应力可根据 求得 将 代入 得   b a x a b R a b a x a b a x a b R ( ) ( ) ( ) 4 2 2 2 2 4 4 2 2 2 4 2 2 2 1 − − = − −  − − 将 = 代入 得 ( ) 2 4 2 2 2 0 1 a x a b S b p  = − − 椭球形壳体的应力分布是随x变化而变化的 ] ( ) ( ) [2 2 4 2 2 2 4 4 2 2 2 0 2 a x a b a a x a b S b p − −  = − − − ( ) 2 4 2 2 2 0 1 a x a b S b p  = − − ( ) 2 0 1 1 b a S pa  顶 = man =

分析： 经向应力 ①从经向应力计算时可看出， 无论 x 为何值，σ1>0,即σ1 都是拉应力 ②顶点处（x=0、 y=b) 顶点处σ1 有最大值 ③边缘处(x=a, y=0) 0 2 0 2 0 1 2 sin 2 sin 2 sin S pR S pR S px = = =     2 0 2 1 1 S p R R + =   1 2 1 0 2 2 R R S pR  = − 0 2 1 2S pR  = (2 ) 2 1 2 0 2 0 2 1 2 0 2 2 R R S pR S pR R R S pR  = − = − 环向应力可根据 求得 将 代入 得   b a x a b R a b a x a b a x a b R ( ) ( ) ( ) 4 2 2 2 2 4 4 2 2 2 4 2 2 2 1 − − = − −  − − 将 = 代入 得 ( ) 2 4 2 2 2 0 1 a x a b S b p  = − − 椭球形壳体的应力分布是随x变化而变化的 ] ( ) ( ) [2 2 4 2 2 2 4 4 2 2 2 0 2 a x a b a a x a b S b p − −  = − − − ( ) 2 4 2 2 2 0 1 a x a b S b p  = − − ( ) 2 0 1 1 b a S pa  顶 = man =

边缘处σ1 有最小值 ④当 a/b=2 时 则： 环向应力σ2 ①顶点处：（x=0,y=b) 且无论 a/b 为何值σ2 顶>0 为拉应力 ②边缘处：（x=a,y=b) 可见σ2 边缘不一定为拉应力，取决于 a/b 的比值 当 a/b 0 为拉应力 当 a/b = 时， σ2 边缘=0 当 a/b > 时， σ2 边缘<0 为压应力 当 a/b = 2 时， -σ2 边缘= σ2 顶= （5）受液压容器的应力分析 a、底部支撑的圆筒 液面受气压作用，具液面 X 处受的压力为 p=p0+Xγ 则: 在容器底部，X=H,环向应力最大 底部支撑的圆筒，液体不产生轴向力，则: 如果是敞开容器，P0=0，则：σ1=0 b、顶部悬挂的圆筒形容器 同理可得： 2 0 2 1 1 S P X R R   +  + = 0 0 2 ( ) S R P X  + = 0 1 1min 2S pa  顶 =  = 0 1 S pa  顶 =  1顶 = 2 1边缘 ] ( ) ( ) [2 2 4 2 2 2 4 4 2 2 2 0 2 a x a b a a x a b S b p − −  = − − − 顶 1顶 0 2 ( ) 2  = = b a S pa [2 ( ) ] 2 2 0 2 b a S pa  边缘 = − [2 ( ) ] 2 2 0 2 b a S pa  边缘 = − 2 2 2 0 S pa 0 0 2max ( ) S R P H  + = 0 0 1 2S P R  = γ 0 0 2 ( ) S R P X  + = + + + _ + _ = = σ2顶 σ2顶 σ2顶 σ2顶 σ2边缘 σ2边缘 σ2边缘 σ2边缘 + + + _ + _ = = σ2顶 σ2顶 σ2顶 σ2顶 σ2边缘 σ2边缘 σ2边缘 σ2边缘

边缘处σ1 有最小值 ④当 a/b=2 时 则： 环向应力σ2 ①顶点处：（x=0,y=b) 且无论 a/b 为何值σ2 顶>0 为拉应力 ②边缘处：（x=a,y=b) 可见σ2 边缘不一定为拉应力，取决于 a/b 的比值 当 a/b 0 为拉应力 当 a/b = 时， σ2 边缘=0 当 a/b > 时， σ2 边缘<0 为压应力 当 a/b = 2 时， -σ2 边缘= σ2 顶= （5）受液压容器的应力分析 a、底部支撑的圆筒 液面受气压作用，具液面 X 处受的压力为 p=p0+Xγ 则: 在容器底部，X=H,环向应力最大 底部支撑的圆筒，液体不产生轴向力，则: 如果是敞开容器，P0=0，则：σ1=0 b、顶部悬挂的圆筒形容器 同理可得： 2 0 2 1 1 S P X R R   +  + = 0 0 2 ( ) S R P X  + = 0 1 1min 2S pa  顶 =  = 0 1 S pa  顶 =  1顶 = 2 1边缘 ] ( ) ( ) [2 2 4 2 2 2 4 4 2 2 2 0 2 a x a b a a x a b S b p − −  = − − − 顶 1顶 0 2 ( ) 2  = = b a S pa [2 ( ) ] 2 2 0 2 b a S pa  边缘 = − [2 ( ) ] 2 2 0 2 b a S pa  边缘 = − 2 2 2 0 S pa 0 0 2max ( ) S R P H  + = 0 0 1 2S P R  = γ 0 0 2 ( ) S R P X  + = + + + _ + _ = = σ2顶 σ2顶 σ2顶 σ2顶 σ2边缘 σ2边缘 σ2边缘 σ2边缘 + + + _ + _ = = σ2顶 σ2顶 σ2顶 σ2顶 σ2边缘 σ2边缘 σ2边缘 σ2边缘

2πRS 0σ1= πR2 (P0+Xγ )+ πR2 (H-X) γ 整理得： 分析： ① σ1 随支撑方式改变 顶部悬挂的圆筒形容器， σ1 与所在位置无关 底部支撑的圆筒， σ1 不受液压影响，仅取决于气压。 ② σ2 不随支撑方式改变 ③ σ2 受度影响，H σ2 对液柱较高的圆筒形容器，可分段计算壁厚 三、边缘应力的 概念及无力矩理论的适用范围 1、边缘应力的 概念 Q、M 叫边缘附加内力 边缘应力：在联接处，由变形不协调而产生的附加内力 系所引起的应力。 2、产生边缘应力的条件 连接的两个部分，受理后变形不同 连接的两个部分互相约束 3、产生边缘应力的实例 （1）壳体与封头联接处经线曲率有突变 (2) 壳体厚度有突变 R S p H 0 0 1 2   + = Q M H-X σ1 πR2 (H-X) γ πR2 (P0+Xγ ) H-X σ1 πR2 (H-X) γ πR2 (P0+Xγ )

2πRS 0σ1= πR2 (P0+Xγ )+ πR2 (H-X) γ 整理得： 分析： ① σ1 随支撑方式改变 顶部悬挂的圆筒形容器， σ1 与所在位置无关 底部支撑的圆筒， σ1 不受液压影响，仅取决于气压。 ② σ2 不随支撑方式改变 ③ σ2 受度影响，H σ2 对液柱较高的圆筒形容器，可分段计算壁厚 三、边缘应力的 概念及无力矩理论的适用范围 1、边缘应力的 概念 Q、M 叫边缘附加内力 边缘应力：在联接处，由变形不协调而产生的附加内力 系所引起的应力。 2、产生边缘应力的条件 连接的两个部分，受理后变形不同 连接的两个部分互相约束 3、产生边缘应力的实例 （1）壳体与封头联接处经线曲率有突变 (2) 壳体厚度有突变 R S p H 0 0 1 2   + = Q M H-X σ1 πR2 (H-X) γ πR2 (P0+Xγ ) H-X σ1 πR2 (H-X) γ πR2 (P0+Xγ )

(3) 圆筒体装有法兰、加强圈等刚性部件 (4)壳体上有集中载荷 （5）壳体上相邻两段材料性质不同组焊接在一起 （6）壳体上相邻两段压力与温度有突变 4、边缘应力的特性 边界效应：边缘应力快速衰减为零的特性 说明边缘应力有很大的“局限性”。 5、无力矩理论应用的范围 在边缘处、支座处、载荷及经线有突变的地方，不能应用无力矩理论计算。 6、容器设计应注意的问题 （1）塑性差的材料应注意边缘应力的影响 （2）塑性好的材料可不必对边缘应力的影响座特殊考虑

(3) 圆筒体装有法兰、加强圈等刚性部件 (4)壳体上有集中载荷 （5）壳体上相邻两段材料性质不同组焊接在一起 （6）壳体上相邻两段压力与温度有突变 4、边缘应力的特性 边界效应：边缘应力快速衰减为零的特性 说明边缘应力有很大的“局限性”。 5、无力矩理论应用的范围 在边缘处、支座处、载荷及经线有突变的地方，不能应用无力矩理论计算。 6、容器设计应注意的问题 （1）塑性差的材料应注意边缘应力的影响 （2）塑性好的材料可不必对边缘应力的影响座特殊考虑