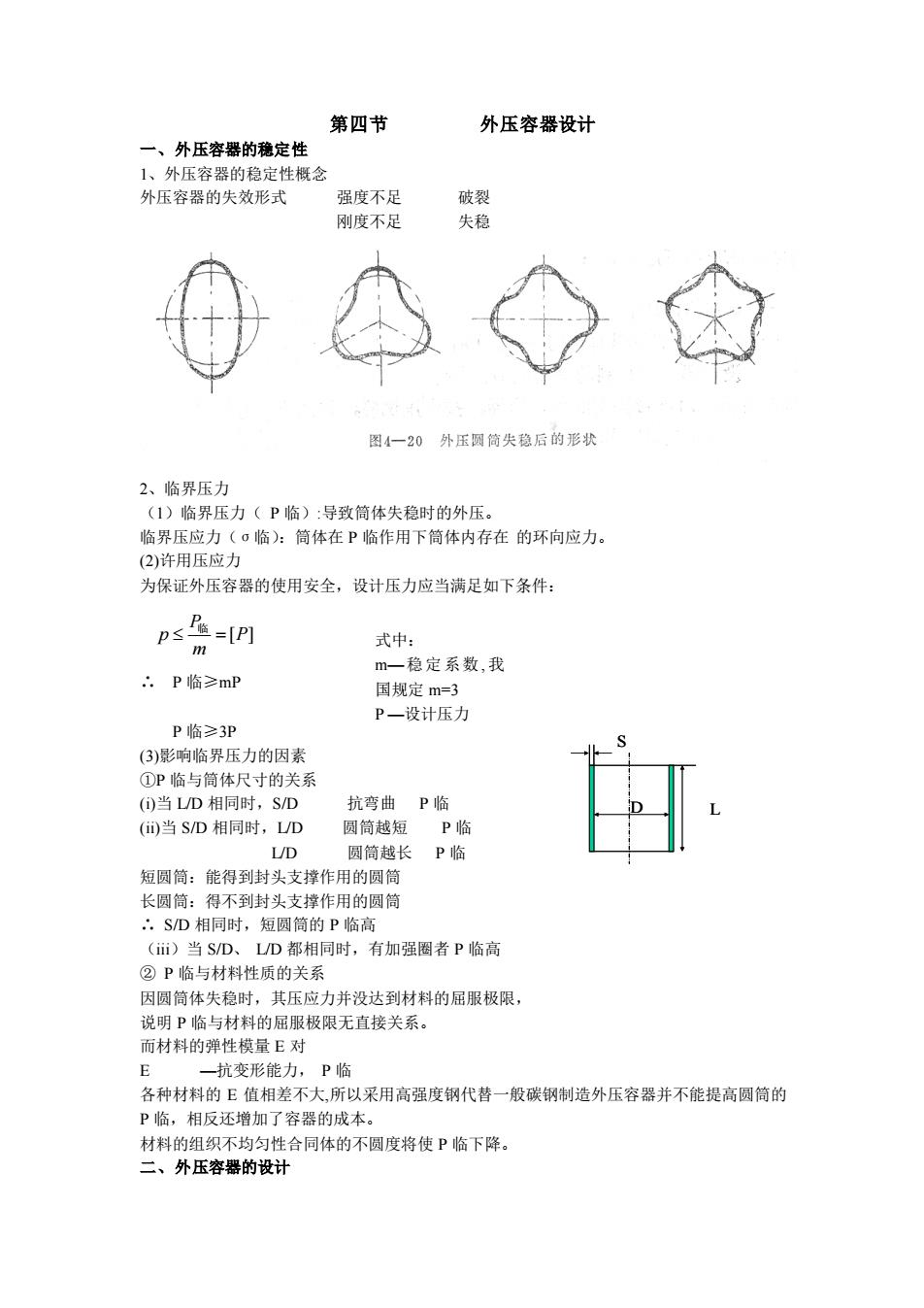
第四节 外压容器设计 一、外压容器的稳定性 1、外压容器的稳定性概念 外压容器的失效形式 强度不足 破裂 刚度不足 失稳 2、临界压力 (1)临界压力( P 临):导致筒体失稳时的外压。 临界压应力(σ临):筒体在 P 临作用下筒体内存在 的环向应力。 (2)许用压应力 为保证外压容器的使用安全,设计压力应当满足如下条件: ∴ P 临≥mP P 临≥3P (3)影响临界压力的因素 ①P 临与筒体尺寸的关系 (i)当 L/D 相同时,S/D 抗弯曲 P 临 (ii)当 S/D 相同时,L/D 圆筒越短 P 临 L/D 圆筒越长 P 临 短圆筒:能得到封头支撑作用的圆筒 长圆筒:得不到封头支撑作用的圆筒 ∴ S/D 相同时,短圆筒的 P 临高 (iii)当 S/D、 L/D 都相同时,有加强圈者 P 临高 ② P 临与材料性质的关系 因圆筒体失稳时,其压应力并没达到材料的屈服极限, 说明 P 临与材料的屈服极限无直接关系。 而材料的弹性模量 E 对 E —抗变形能力, P 临 各种材料的 E 值相差不大,所以采用高强度钢代替一般碳钢制造外压容器并不能提高圆筒的 P 临,相反还增加了容器的成本。 材料的组织不均匀性合同体的不圆度将使 P 临下降。 二、外压容器的设计 [P] m P p = 临 式中: m—稳定系数, 我 国规定 m=3 P —设计压力 D L S
第四节 外压容器设计 一、外压容器的稳定性 1、外压容器的稳定性概念 外压容器的失效形式 强度不足 破裂 刚度不足 失稳 2、临界压力 (1)临界压力( P 临):导致筒体失稳时的外压。 临界压应力(σ临):筒体在 P 临作用下筒体内存在 的环向应力。 (2)许用压应力 为保证外压容器的使用安全,设计压力应当满足如下条件: ∴ P 临≥mP P 临≥3P (3)影响临界压力的因素 ①P 临与筒体尺寸的关系 (i)当 L/D 相同时,S/D 抗弯曲 P 临 (ii)当 S/D 相同时,L/D 圆筒越短 P 临 L/D 圆筒越长 P 临 短圆筒:能得到封头支撑作用的圆筒 长圆筒:得不到封头支撑作用的圆筒 ∴ S/D 相同时,短圆筒的 P 临高 (iii)当 S/D、 L/D 都相同时,有加强圈者 P 临高 ② P 临与材料性质的关系 因圆筒体失稳时,其压应力并没达到材料的屈服极限, 说明 P 临与材料的屈服极限无直接关系。 而材料的弹性模量 E 对 E —抗变形能力, P 临 各种材料的 E 值相差不大,所以采用高强度钢代替一般碳钢制造外压容器并不能提高圆筒的 P 临,相反还增加了容器的成本。 材料的组织不均匀性合同体的不圆度将使 P 临下降。 二、外压容器的设计 [P] m P p = 临 式中: m—稳定系数, 我 国规定 m=3 P —设计压力 D L S

1、理论公式计算法 (1)壁厚的计算 钢制长圆 : 钢制短圆筒: 将 P 临≥3P 代入可得 1)钢制长圆筒: mm 2)钢制短圆筒: mm 3)刚性圆筒 一般:S L 的圆筒叫刚性圆筒 一般不存在失稳,因此只考虑强度即可 (2)临界长度 L 临 当短圆筒的长度大到某一临界值 L 临时,封头对筒体的支撑作用将完全消失,这时短圆筒 的 P 临将下降到长圆筒的 P 临, 即: 解得: 为区别长短圆筒的临界长度 当 LL 临时,为长圆筒 (3)用理论公式设计的步骤 ①设理论壁厚为 S。,并选定材料 ②计算 L 临 ③比较确定圆筒类型 L 与 L 临,确定圆筒类型 ④根据圆筒类型计算 P 临 ⑤计算许用应力[P]= P 临/3 比较:设计压力 P 与 P 临 若 P≤[P],且接近,假设的 S。合适 若 p>[p],这说明假设 S。过薄,需重新假设 ⑥实际壁厚 S=S。+C 2、图算法 (1)算图的由来 临界压应力: 0 3 2.2 ( ) D S p临 = E D L D S P E 0 2.5 ( ) 临 = 2.6 C E P S = D3 + 2.2 3 C D L E P S = D + 0.4 ) 2.6 3 ( D L D S E 0 2.5 ( ) 2.6 0 3 2.2 ( ) D S = E 0 1.17 S D L临 = D 2S0 P临D 临 =
1、理论公式计算法 (1)壁厚的计算 钢制长圆 : 钢制短圆筒: 将 P 临≥3P 代入可得 1)钢制长圆筒: mm 2)钢制短圆筒: mm 3)刚性圆筒 一般:S L 的圆筒叫刚性圆筒 一般不存在失稳,因此只考虑强度即可 (2)临界长度 L 临 当短圆筒的长度大到某一临界值 L 临时,封头对筒体的支撑作用将完全消失,这时短圆筒 的 P 临将下降到长圆筒的 P 临, 即: 解得: 为区别长短圆筒的临界长度 当 LL 临时,为长圆筒 (3)用理论公式设计的步骤 ①设理论壁厚为 S。,并选定材料 ②计算 L 临 ③比较确定圆筒类型 L 与 L 临,确定圆筒类型 ④根据圆筒类型计算 P 临 ⑤计算许用应力[P]= P 临/3 比较:设计压力 P 与 P 临 若 P≤[P],且接近,假设的 S。合适 若 p>[p],这说明假设 S。过薄,需重新假设 ⑥实际壁厚 S=S。+C 2、图算法 (1)算图的由来 临界压应力: 0 3 2.2 ( ) D S p临 = E D L D S P E 0 2.5 ( ) 临 = 2.6 C E P S = D3 + 2.2 3 C D L E P S = D + 0.4 ) 2.6 3 ( D L D S E 0 2.5 ( ) 2.6 0 3 2.2 ( ) D S = E 0 1.17 S D L临 = D 2S0 P临D 临 =
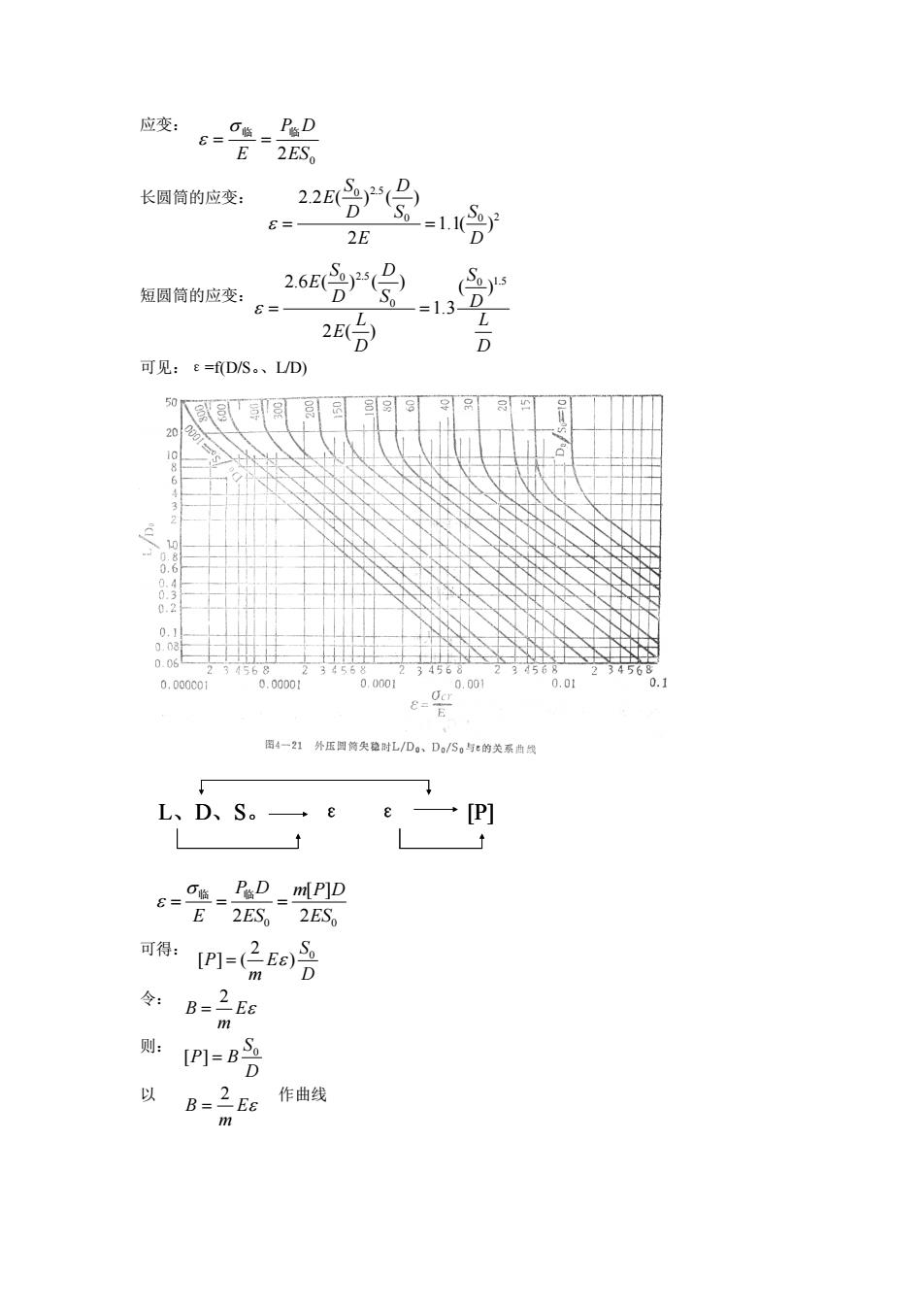
应变: 长圆筒的应变: 短圆筒的应变: 可见:ε=f(D/S。、L/D) 可得: 令: 则: 以 作曲线 L、D、S。 ε ε [P] 2ES0 P D E 临 临 = = 0 0 2 0 2.5 1.1( ) 2 2.2 ( ) ( ) D S E S D D S E = = D L D S D L E S D D S E 0 1.5 0 0 2.5 ( ) 1.3 2 ( ) 2.6 ( ) ( ) = = 0 2 0 [ ] 2 ES m P D ES P D E = = = 临 临 D S E m P 0 ) 2 [ ] = ( E m B 2 = D S P B 0 [ ] = E m B 2 =
应变: 长圆筒的应变: 短圆筒的应变: 可见:ε=f(D/S。、L/D) 可得: 令: 则: 以 作曲线 L、D、S。 ε ε [P] 2ES0 P D E 临 临 = = 0 0 2 0 2.5 1.1( ) 2 2.2 ( ) ( ) D S E S D D S E = = D L D S D L E S D D S E 0 1.5 0 0 2.5 ( ) 1.3 2 ( ) 2.6 ( ) ( ) = = 0 2 0 [ ] 2 ES m P D ES P D E = = = 临 临 D S E m P 0 ) 2 [ ] = ( E m B 2 = D S P B 0 [ ] = E m B 2 =
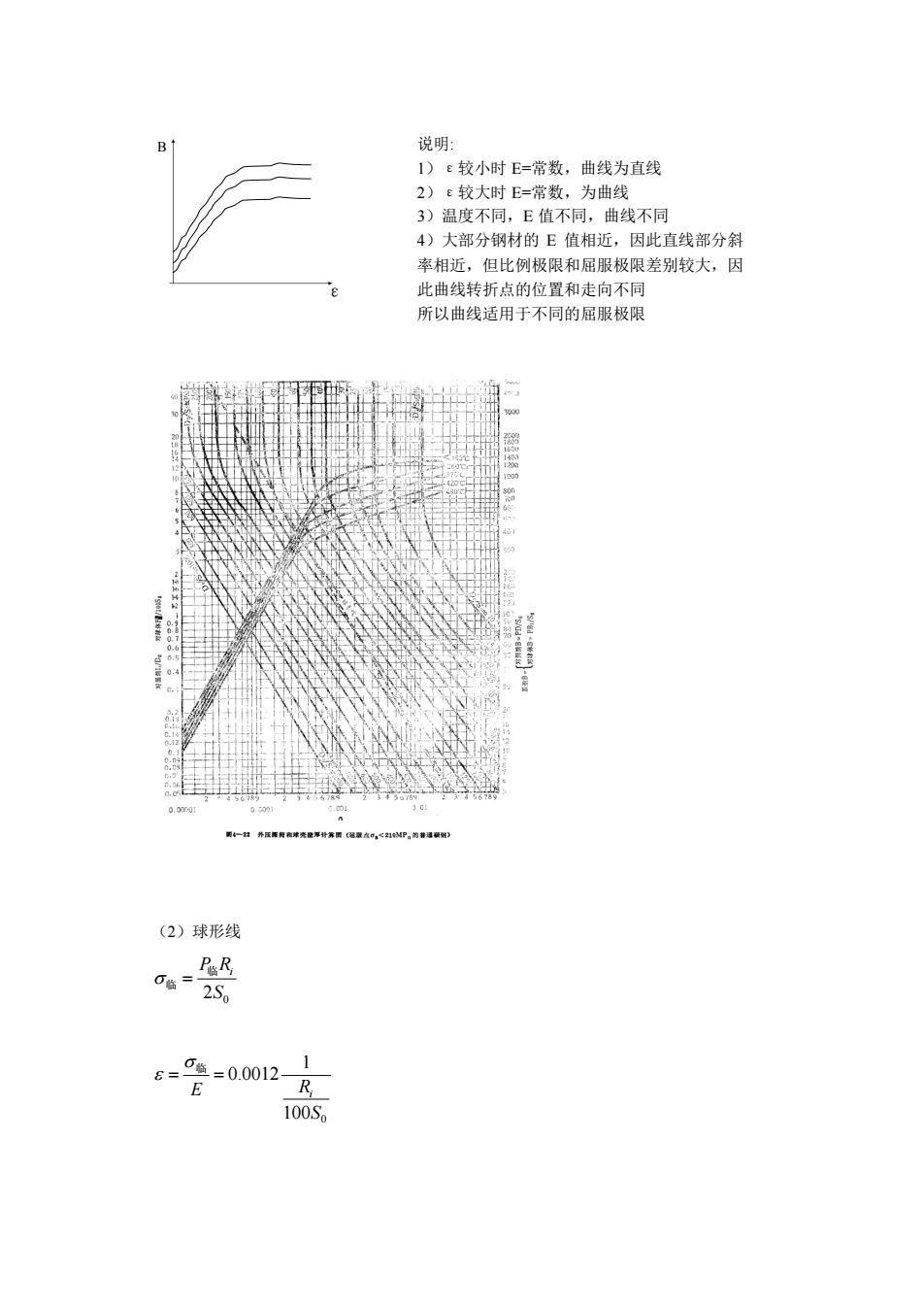
B ε 说明: 1)ε较小时 E=常数,曲线为直线 2)ε较大时 E=常数,为曲线 3)温度不同,E 值不同,曲线不同 4)大部分钢材的 E 值相近,因此直线部分斜 率相近,但比例极限和屈服极限差别较大,因 此曲线转折点的位置和走向不同 所以曲线适用于不同的屈服极限 (2)球形线 2S0 P临Ri 临 = 100 0 1 0.0012 S E Ri = = 临
B ε 说明: 1)ε较小时 E=常数,曲线为直线 2)ε较大时 E=常数,为曲线 3)温度不同,E 值不同,曲线不同 4)大部分钢材的 E 值相近,因此直线部分斜 率相近,但比例极限和屈服极限差别较大,因 此曲线转折点的位置和走向不同 所以曲线适用于不同的屈服极限 (2)球形线 2S0 P临Ri 临 = 100 0 1 0.0012 S E Ri = = 临

(3)算图的应用 ①假设 S。 ,计算 L/D。、D。/S。 ②根据材料σ临 确定线图 ③根据 L/D。、D。/S。确定ε ④根据ε和设计温度 B ⑤计算[P]=B S/D。 ⑥比较:若 P≤[P],且接近,假设 S。合适 若 P>[P],假设 S。过薄,重设 ⑦实际壁厚 S=S。+ C
(3)算图的应用 ①假设 S。 ,计算 L/D。、D。/S。 ②根据材料σ临 确定线图 ③根据 L/D。、D。/S。确定ε ④根据ε和设计温度 B ⑤计算[P]=B S/D。 ⑥比较:若 P≤[P],且接近,假设 S。合适 若 P>[P],假设 S。过薄,重设 ⑦实际壁厚 S=S。+ C