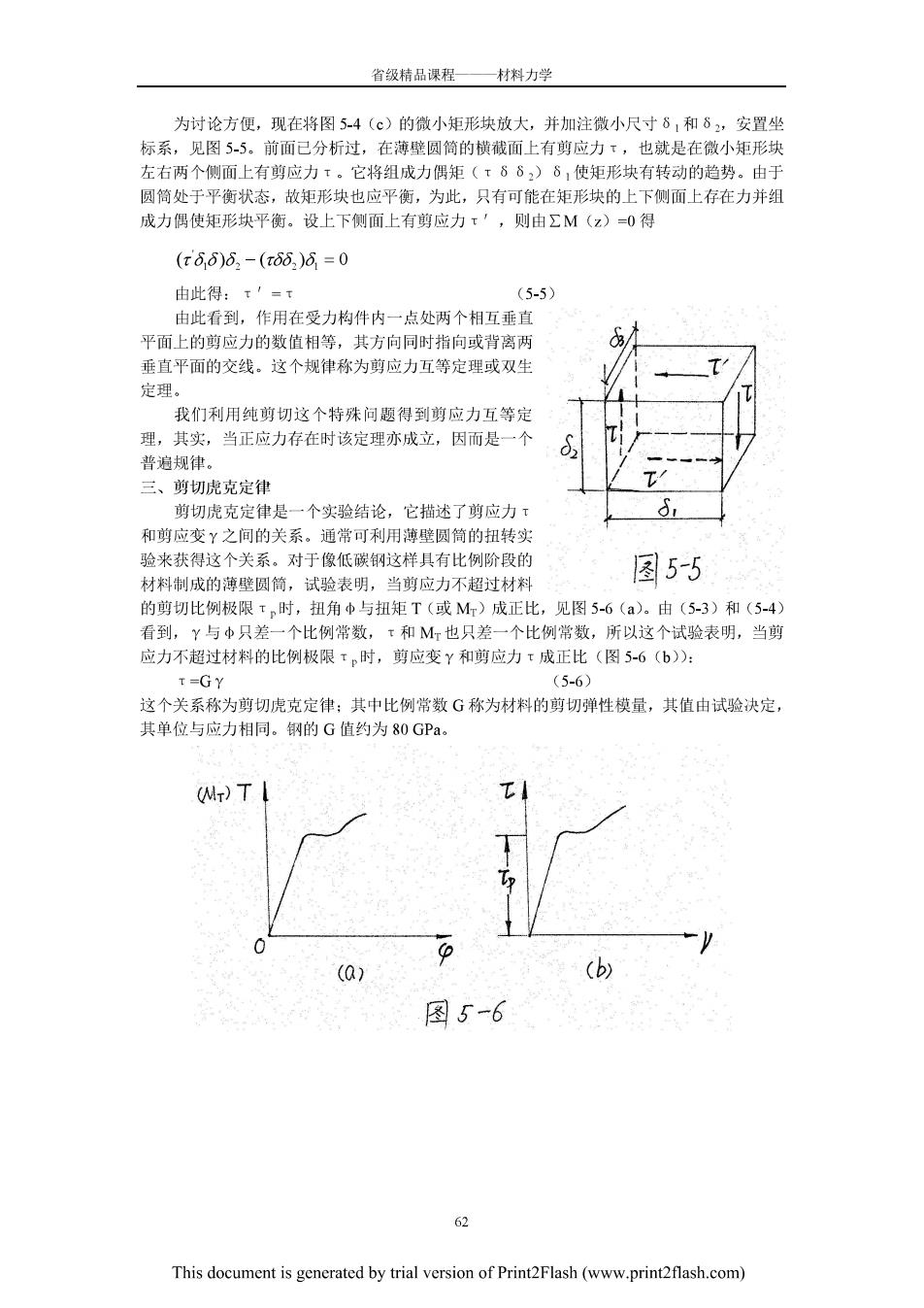
省级精品课程—材料力学 为讨论方便，现在将图54（©）的微小矩形块放大，并加注微小尺寸8，和8，安置坐 标系，见图55。前面已分析时，在兼壁圆简的横战面上有前应力，也就是在微小矩形块 左右两个侧面上有剪应力 。它将组成力偶知 (166)61使矩形块有转动的趋势。由于 圆筒处于平衡状态，故矩形块也应平衡，为此，只有可能在矩形块的上下侧面上存在力并组 成力偶使矩形块平衡。设上下侧面上有剪应力t',则由ΣM(z)=0得 (r66)5.-(r66,)8=0 由此得：t=t 5-5 由此看到，作用在受力构件内一点处两个相互垂 平面上的剪应力的数值相等，其方向同时指向或背离两 垂直平面的交线。这个规律称为剪应力互等定理或双生 定理。 我们利用纯煎切杖个殊间题得到前应力石等完 理，其实，当正应力存在时该定理亦成立， 因而是 -个 普遍规律。 三、剪切虎克定律 剪切虎克定律是一个实验结论，它描述了剪应力T 和道应变y之间的关系。涌常可利用薄壁圆简的邦书头 验来获得这个关系。对于像低碳钢这样具有比例阶段的 材料制成的薄壁圆筒，试验表明，当剪应力不超过材料 图5-5 的剪切比例极限rn时，扭角中与扭矩T(或Mr)成正比，见图5-6(a).由(5-3)和(5-4 看到，Y与中只差一个比例常数，t和M也只差一个比例常数，所以这个试验表明，当剪 应力不超过材料的比例极限τ。时，剪应变Y和剪应力τ成正比（图5-6(b): (5-6) 这个关系称为剪切虎克定律：其中比例常数G称为材料的剪切弹性模量，其值由试验决定 其单位与应力相同.钢的G值约为80GPa, (M)T 图5-6 62 This document is generated by trial version of Print2Flash(www.print2flash.com)