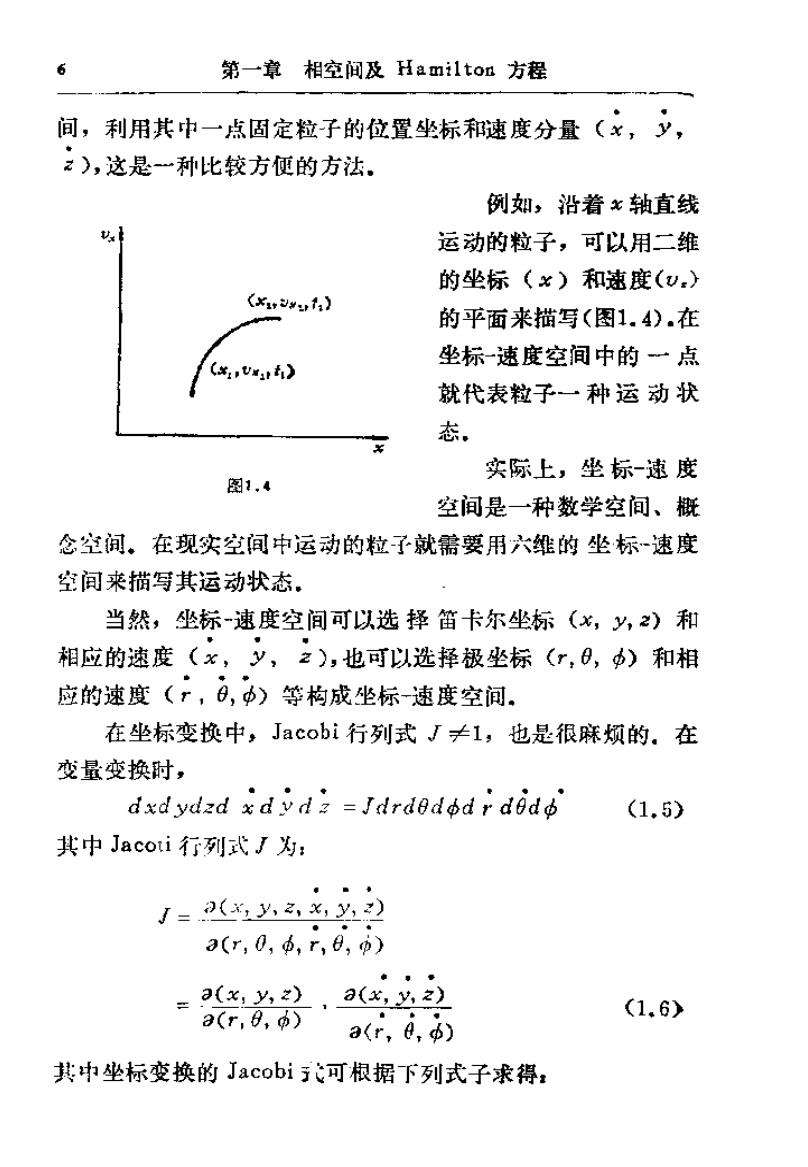
6 第一章相空间及Hamilton方程 间，利用其中一点固定粒子的位置坐标和速度分量（￥，y, 之)，这是一种比较方便的方法。 例知，沿着x轴直线 运动的粒子，可以用二维 的坐标(×)和速箕(v. (x￥12】 的平面来描写（图1.4）.在 坐标速度空间中的一点 (*:,Umt) 就代表粒子一种运动状 态 实际上，坐标-速度 图1,4 空间是一种数学空间、概 念空间。在现实空间中运动的粒子就需要用六维的坐标速度 空间来描写其运动状态。 当然，坐标-速度空间可以选择笛卡尔坐标(x,y,)和 相应的速度（x,y,之)，也可以选择极坐标(r,0,)和相 应的速度（r,6,)等构成坐标速度空间 在坐标变换中，Jacobi行列式J≠1，也是很麻烦的.在 变量变换时， dxdydzd xdyd=Idrdedodr dedd (1.5) 其中Jacoti行列式J为： J=(￥2y3x,y) a(r,0,,r,8,p) 3(￥，y,2),a(,必2） a(r,8,) (1.6) a(r,0,$ 其中坐标变换的Jacobi可根据下列式子求得：