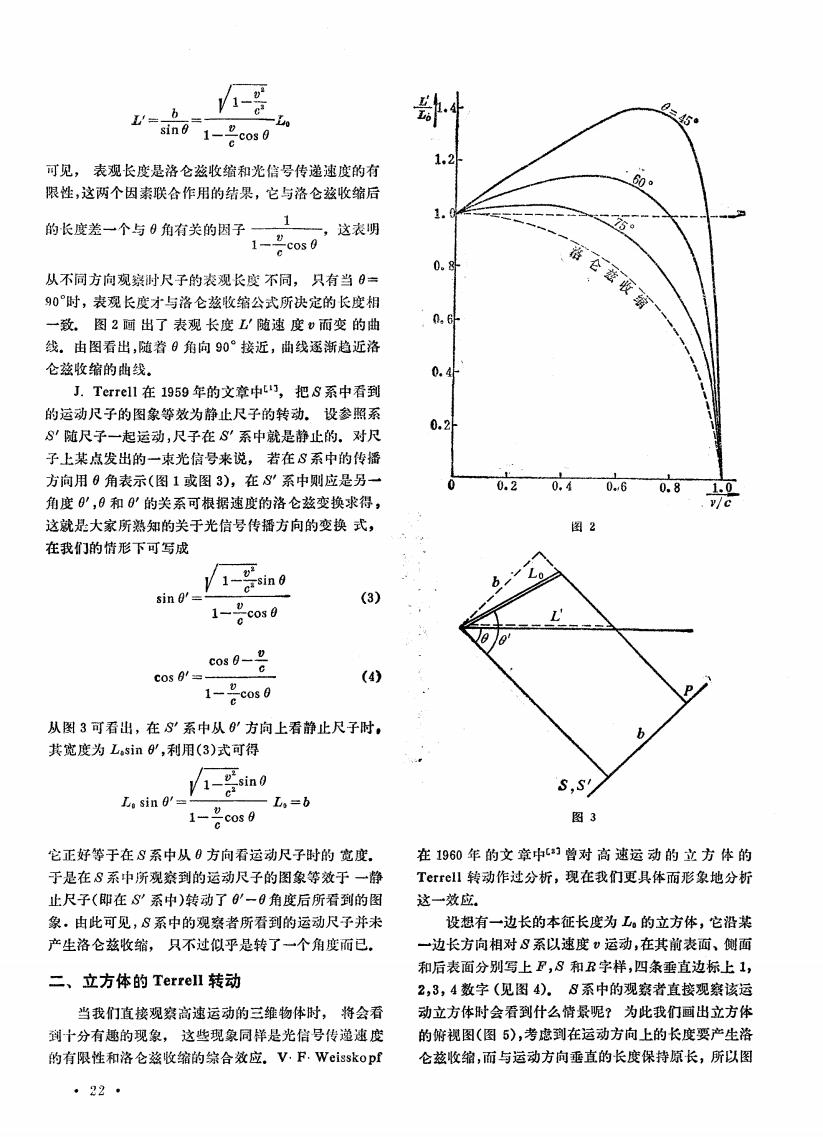
1、2 V=b 0=45° sin61-”c os0 可见，表观长度是洛仑兹收缩和光信号传递速度的有 限性，这两个因素联合作用的结果，它与洛仑兹收缩后 60 的长度差一个与0角有关的因子1 1、 一，这表明 75 ccos 从不同方向观浆时尺子的表观长度不同，只有当9= 90时，表观长度才与洛仑兹收缩公式所决定的长度相 落仑兹暇缩 一致.图2画出了表观长度L随速度而变的曲 线。由图看出，随着9角向90°接近，曲线逐渐趋近洛 仑兹收缩的曲线。 0.4 J.Terrel1在1959年的文章中t,把8系中看到 的运动尺子的图象等效为静止尺子的转动。设参照系 0.2 S”随尺子一起运动，尺子在S'系中就是静止的。对尺 子上某点发出的一束光信号来说，若在8系中的传播 方向用0角表示（图1或图3），在S”系中则应是另一 0.2 0。 06 0.8 1.0 角度日'，9和0'的关系可根据速度的洛仑兹变换求得， V/c 这就是大家所熟知的关于光信号传播方向的变换式， 图2 在我们的情形下可写成 1 osin 0 sin 0'= 1 (3) c cos0 c03B" cos ! c (4) 1、0 cos0 从图3可看出，在S系中从'方向上看静止尺子时， b 其宽度为Lsin0,利用(3)式可得 sin 1- S,S! Lo sin 0=- 1也 -L,=b ccos g 图3 它正好等于在8系中从0方向看运动尺子时的宽度. 在1960年的文章中)曾对高速运动的立方体的 于是在8系中所观笨到的运动尺子的图象等效于一静 Terrell转动作过分析，现在我们更具体而形象地分析 止尺子（即在S”系中）转动了'一0角度后所看到的图 这一效应. 象。由此可见，8系中的观察者所看到的运动尺子并米 设想有一边长的本征长度为工。的立方体，它沿某 产生洛仑兹收缩，只不过似乎是转了一个角度而已. 一边长方向相对8系以速度)运动，在其前表面、侧面 和后表面分别写上F,8和R字样，四条垂直边标上1， 二、立方体的Terrell转动 2,3,4数字（见图4）。8系中的观察者直接观察该运 当我们直接观察高速运动的三雏物体时，将会看 动立方体时会看到什么情景呢？为此我们画出立方体 到十分有趣的现象，这些现象同样是光信号传递速度 的俯视图（图5），考虑到在运动方向上的长度要产生洛 的有限性和洛仑兹收缩的综合效应。V,F.Weissko pf 仑兹收缩，而与运动方向垂直的长度保持原长，所以图 ·22可见， 表观长度是洛 仑兹 g 收缩 和光 信号传递 速度 的有 限性 ，这两个 因素联合作用的结果 ，它与洛 仑兹收缩后 的长度差 一个与 0角有关的 因子 —— ～ 一，这表 明 1一 cos0 从不同方向观察时尺子 的表观 毖度 不同， 只有当 0= 9O。时 ，表观 长度才与洛仑兹收缩公式所决定的长度相 一 致． 图 2画 出了 表观 长度 随速 度 而 变 的曲 线． 由图看出 ，随着 0角向 90。按近 ，曲线逐渐趋 近洛 仑兹收缩的 曲线． J．Terrell在 1959年 的文章中【l】， 把 系中看到 的运动尺 子的 图象等效为静止尺子的转动． 设参照系 随尺 子一起运动 ，尺子在 系中就是静止的．对尺 子上某点发 出的一束光信号来说 ， 若在 系 中的传播 方向用 0角表示 (图 1或 图 3)，在 系 中则应是另一 角度 0，日和 0 的关系可根据速度的洛仑兹变换求得 ， 这就是大家所熟知的关于光信号传播方向的变换 式， 在我们的情形下可写成 sin日=／— 一sin (3) 卜詈coOs0 COS =—兰二一 (4)> 1一 旦cos0 从 图 3可看 出，在 系中从 口 方向上看静止 尺子时． 其宽度为 五。sin日，利用(3)式可得 0 b -Lt CO S 口sin ——_=_=——一 五o= 1一 一 毋 它正好等于在 系中从 0方 向看运动尺子时的 宽度． 于 是在 系中所观察到的运动尺子的 图象等效于 一静 止尺子 (即在 系中)转 动了 口一口角度后所看到的 图 象 ．由此可见 ， 系 中的观察者所看到的运动尺子并未 产生洛 仑兹 收缩 ， 只不过似乎是转了一个角度而 已． 二、立方体的 Terrell转动 当我们直接观察高速运动的三维物体时， 将会看 到十分有趣的现象， 这些现象同样是光 信号传递速度 的有限性和洛仑兹收缩的综合效应．V·F·Weisskopf 圈 Z 图 3 在 1960年 的文 章 中 曾对 高 速运 动 的 立 方 俸 的 Terrell转动作过分析 ，现在我们更具体而形象地分析 这一效应． 设想有一边长的本征长度为 。的立方体 ，它沿某 一 边长方 向相对 系以速度 口运动 ，在其 前表面 、侧面 和后表面 分别写上 ， 和 字样 ，四条垂直边标上 1， 2，3，4数字 (见图 4)． 系中的观察者直接观察该运 动立方体时会 看到什么 情景呢? 为 此我们 画出立 方体 的俯视图(图 5)，考虑到在运动方向上的长度 要产生浴 仑兹收缩 ，而 与运动方向垂直 的长度保持原 长，所 以图