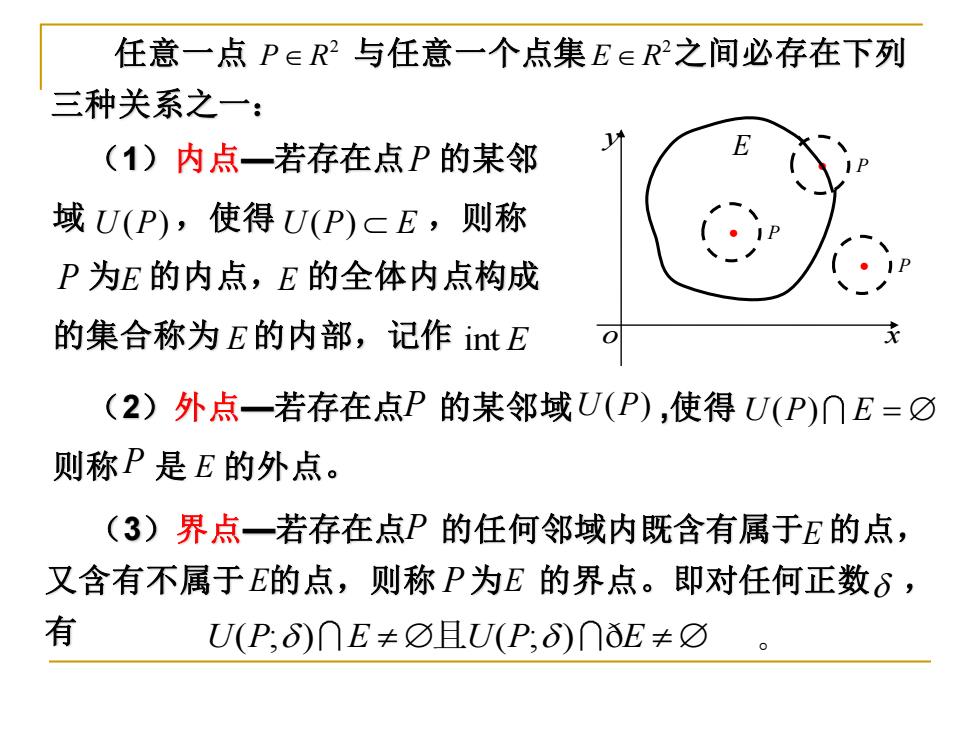
任意一点P∈R2与任意一个点集E∈R2之间必存在下列 三种关系之一： (1)内点一若存在点P的某邻 域U(P),使得U(P)cE,则称 P为E的内点，E的全体内点构成 的集合称为E的内部，记作intE (2)外点一若存在点P的某邻域U(P),使得U(P)∩E=O 则称P是E的外点。 (3)界点一若存在点P的任何邻域内既含有属于E的点， 又含有不属于E的点，则称P为E的界点。即对任何正数δ， 有 U(P,6)∩E≠☑且U(P,6)∩ǒE≠☑任意一点 与任意一个点集 之间必存在下列 三种关系之一： 2 P R  2 E R  y o x （ E 1）内点—若存在点 的某邻 域 ，使得 ，则称 为 的内点， 的全体内点构成 的集合称为 的内部，记作 P U P( ) U P E ( )  P E E E int E • P （2）外点—若存在点 的某邻域 ,使得 则称 是 的外点。 U P( ) U P E ( ) =  P E P • P • P （3）界点—若存在点 的任何邻域内既含有属于 的点， 又含有不属于 的点，则称 为 的界点。即对任何正数 ， 有 U P E U P E ( ; ) ( ; )       且 ð P P E E E 