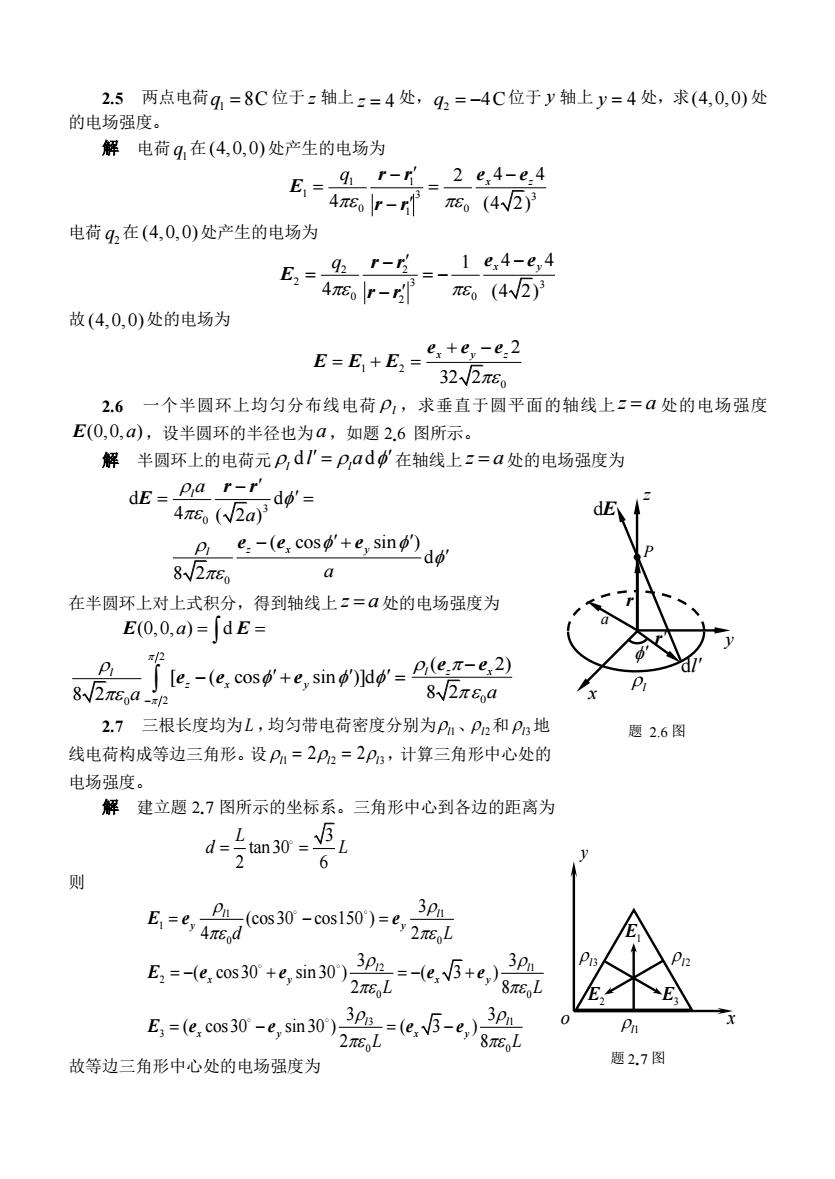
2.5两点电荷q=8C位于：轴上z=4处，2=-4C位于y轴上y=4处，求(4,0,0)处 的电场强度。 解电荷g在(4,0,0)处产生的电场为 子品 电荷42在(4,0,0)处产生的电场为 E=9- 1e,4-e,4 高-守而 故(4,0,0)处的电场为 E-E+B=ete-e.2 32√2π6。 2.6一个半圆环上均匀分布线电荷P,求垂直于圆平面的轴线上2=a处的电场强度 E(0,0,a),设半圆环的半径也为a,如题2.6图所示。 解半圆环上的电荷元P,dI'=P,ad'在轴线上z=a处的电场强度为 E-w- dE pe.-(e.cose,sind 82π5 a 在半圆环上对上式积分，得到轴线上z=a处的电场强度为 E(0,0,a)=dE- P le.-(e,cos'+e,sindee,2) 82π6an 8W2π8a 2.7三根长度均为L,均匀带电荷密度分别为P1、P2和p地 题2.6图 线电荷构成等边三角形。设Pm=2P2=2Ps,计算三角形中心处的 由场强度。 解建立题2.7图所示的坐标系。三角形中心到各边的距离为 d=an30=5L 6 3p1 E=6,4Ccs30-s150)=6,22 Eks+n0益e6+叠 E,=化，60s30-t,n30)i 3p%=e,5-,8 3p 故等边三角形中心处的电场强度为 题2.7图2.5 两点电荷 1 q = 8C 位于 z 轴上 z = 4 处， 2 q = −4C 位于 y 轴上 y = 4 处，求 (4,0,0) 处 的电场强度。 解 电荷 1 q 在 (4,0,0) 处产生的电场为 1 1 1 3 3 0 0 1 2 4 4 4 (4 2) q x z   −  − = = −  r r e e E r r 电荷 2 q 在 (4,0,0) 处产生的电场为 2 2 2 3 3 0 0 2 1 4 4 4 (4 2) q x y   −  − = = − −  r r e e E r r 故 (4,0,0) 处的电场为 1 2 0 2 32 2 x y z  + − = + = e e e E E E 2.6 一个半圆环上均匀分布线电荷  l ，求垂直于圆平面的轴线上 z a = 处的电场强度 E(0,0, ) a ，设半圆环的半径也为 a ，如题 2.6 图所示。 解 半圆环上的电荷元 d d l l    l a   = 在轴线上 z a = 处的电场强度为 3 0 d d 4 ( 2 ) l a a    −  = =  r r E 0 ( cos sin ) d 8 2 l z x y a      − +   e e e 在半圆环上对上式积分，得到轴线上 z a = 处的电场强度为 (0,0, ) d a = =  E E 2 0 2 [ ( cos sin )]d 8 2 l z x y a        − − + =     e e e 0 ( 2) 8 2 l z x a    e e − 2.7 三根长度均为 L ，均匀带电荷密度分别为 l1、l 2 和 l3 地 线电荷构成等边三角形。设 l1 = 2 2l = 3 2l ，计算三角形中心处的 电场强度。 解 建立题 2.7 图所示的坐标系。三角形中心到各边的距离为 3 tan 30 2 6 L d L = = 则 1 1 1 0 0 3 (cos30 cos150 ) 4 2 l l y y d L     E e e = − = 2 1 2 0 0 3 3 ( cos30 sin 30 ) ( 3 ) 2 8 l l x y x y L L     E e e e e = − + = − + 3 1 3 0 0 3 3 ( cos30 sin 30 ) ( 3 ) 2 8 l l x y x y L L     E e e e e = − = − 故等边三角形中心处的电场强度为 a z x y dl  l P dE r r 题 2.6 图 l 2 l1 l3 x y o E1 E2 E3 题 2.7 图