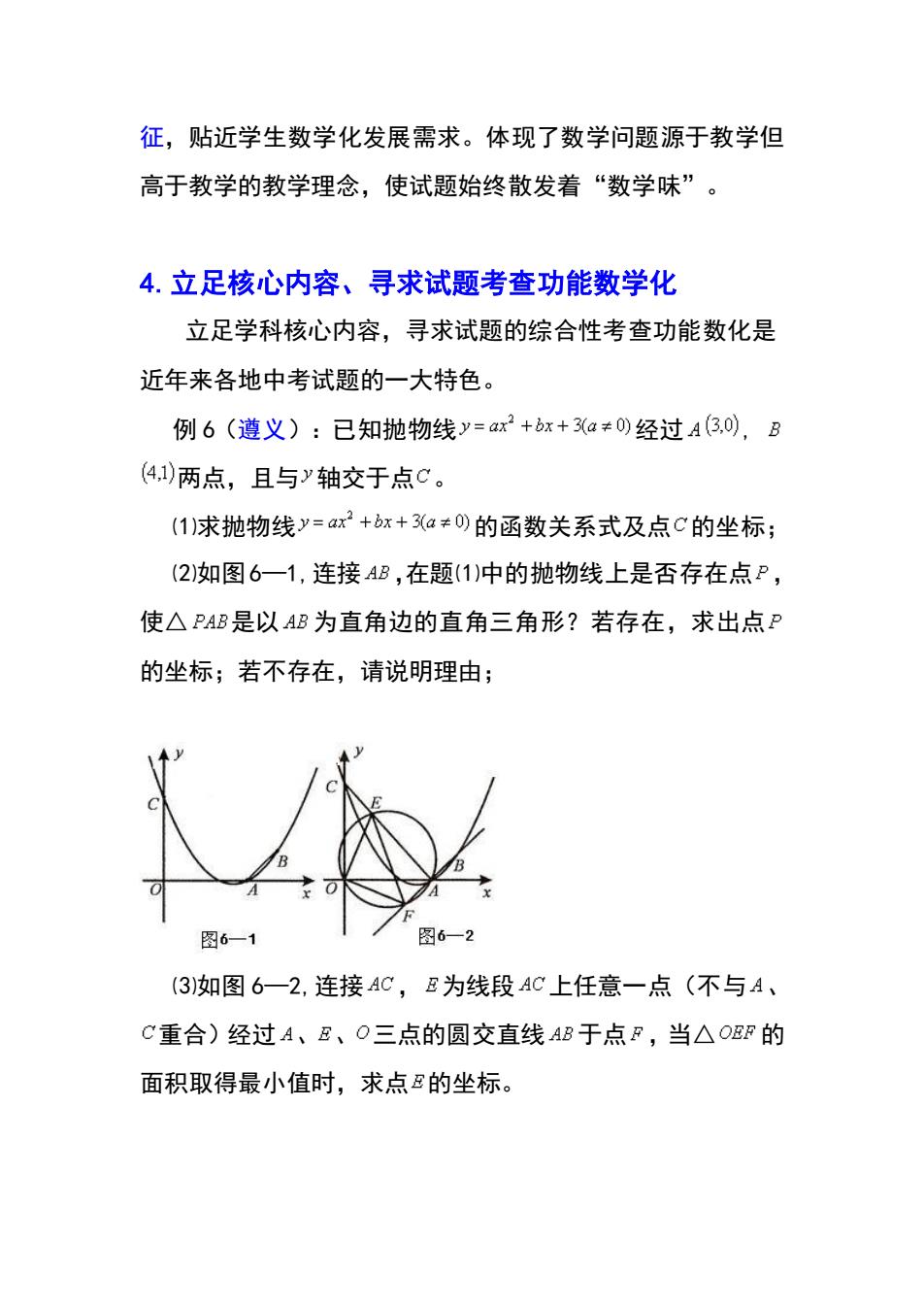
征，贴近学生数学化发展需求。体现了数学问题源于教学但 高于教学的教学理念，使试题始终散发着“数学味”。 4.立足核心内容、寻求试题考查功能数学化 立足学科核心内容，寻求试题的综合性考查功能数化是 近年来各地中考试题的一大特色。 例6（遵义）：已知抛物线y=ax2+bx+3a≠0)经过A(3,0),B (4,1)两点，且与y轴交于点C。 (1)求抛物线y=ax2+x+a≠0)的函数关系式及点C的坐标； (2)如图6一1，连接AB,在题(1)中的抛物线上是否存在点P, 使△PAB是以AB为直角边的直角三角形？若存在，求出点P 的坐标；若不存在，请说明理由： 图6一1 图6一2 (3如图6一2，连接AC,E为线段AC上任意一点（不与A、 C重合)经过A、E、O三点的圆交直线AB于点F,当△OEF的 面积取得最小值时，求点的坐标。征，贴近学生数学化发展需求。体现了数学问题源于教学但 高于教学的教学理念，使试题始终散发着“数学味”。 4.立足核心内容、寻求试题考查功能数学化 立足学科核心内容，寻求试题的综合性考查功能数化是 近年来各地中考试题的一大特色。 例 6（遵义）：已知抛物线 经过 , 两点，且与 轴交于点 。 ⑴求抛物线 的函数关系式及点 的坐标； ⑵如图6—1,连接 ，在题⑴中的抛物线上是否存在点 ， 使△ 是以 为直角边的直角三角形？若存在，求出点 的坐标；若不存在，请说明理由； ⑶如图 6—2,连接 ， 为线段 上任意一点（不与 、 重合）经过 、 、 三点的圆交直线 于点 ，当△ 的 面积取得最小值时，求点 的坐标