
2011年数学中考试题分类赏析 在本年度中考试题中,不少命题专家从应试者的心理承 受能力出发,设计出了不少既考查学生对数学核心概念、思 想方法的理解及运用水平,又使学生在考试过程中经历数学 化的过程,从而提高自身的文化素养和创新意识的试题。 1.传承数学文化、让学生体验数学化的科学价值 新课标指出:“数学是人类的一种文化,它的内容、思 想、方法和语言是现代文明的重要组成部分”。“是人类 社会进步的产物,也是推动社会发展的动力”。中考作为一 种社会文化现象,必然要从属和服务于社会意识形态和特定 的文化结构,必须要承载社会赋予其特定的功能一数学 化。 例1:(温州)我国汉代数学家赵爽为了证明勾股定理, 创制了一副“弦图”,后人称其为“赵爽弦图”(如图1一1)。 图1一2由弦图变化得到,它是由八个全等的直角三角形拼 接而成。记图1一2中正方形ABCD,正方形EFCH,正方形MWKT 的面积分别为,若++心=10,则8的值是一
2011 年数学中考试题分类赏析 在本年度中考试题中,不少命题专家从应试者的心理承 受能力出发,设计出了不少既考查学生对数学核心概念、思 想方法的理解及运用水平,又使学生在考试过程中经历数学 化的过程,从而提高自身的文化素养和创新意识的试题。 1.传承数学文化、让学生体验数学化的科学价值 新课标指出:“数学是人类的一种文化,它的内容、思 想、方法和语言是现代文明的重要组成部分”。 “是人类 社会进步的产物,也是推动社会发展的动力”。中考作为一 种社会文化现象,必然要从属和服务于社会意识形态和特定 的文化结构,必须要承载社会赋予其特定的功能——数学 化。 例 1:(温州)我国汉代数学家赵爽为了证明勾股定理, 创制了一副“弦图”,后人称其为“赵爽弦图”(如图 1—1)。 图 1—2 由弦图变化得到,它是由八个全等的直角三角形拼 接而成。记图 1—2 中正方形 ,正方形 ,正方形 的面积分别为 ,若 =10,则 的值是

图1一1 图1-2 解析:由题意可知,=a+,=C2,=6-a以。又由 +号+网=10,易得:品的值是号 赏析:勾股定理是人类最伟大的十个科学发现之一。有十 分悠久的历史,两千多年来,人们对勾股定理的证明颇感兴 趣,因为这个定理太贴近人们的生活实际,以至于古往今来, 下至平民百姓,上至帝王总统都愿意探讨和研究它。赵爽的 证明可谓别具匠心,极富创新意识。他用几何图形的截、割、 拼、补来证明代数式之间的恒等关系,既具严密性,又具直 观性,为中国古代以形证数、形数统一、代数和几何紧密结 合、互不可分的独特风格树立了一个典范。学生通过解此题, 进一步体验了形数统一的思想方法,又一次经历了认识勾股 定理的数学化过程。受到优秀文化的熏陶,传承了中华民族 悠悠五千年文化史。 2.关注问题情境、让学生经历数学化的思维过 程 在命制中考试题中,如何创设试题情境是一种智慧的挑 战。试题情境需要命题教师对教学本身进行周密思考与精心
解析:由题意可知, , , 。又由 =10,易得: 的值是 赏析:勾股定理是人类最伟大的十个科学发现之一。有十 分悠久的历史,两千多年来,人们对勾股定理的证明颇感兴 趣,因为这个定理太贴近人们的生活实际,以至于古往今来, 下至平民百姓,上至帝王总统都愿意探讨和研究它。赵爽的 证明可谓别具匠心,极富创新意识。他用几何图形的截、割、 拼、补来证明代数式之间的恒等关系,既具严密性,又具直 观性,为中国古代以形证数、形数统一、代数和几何紧密结 合、互不可分的独特风格树立了一个典范。学生通过解此题, 进一步体验了形数统一的思想方法,又一次经历了认识勾股 定理的数学化过程。受到优秀文化的熏陶,传承了中华民族 悠悠五千年文化史。 2. 关注问题情境、让学生经历数学化的思维过 程 在命制中考试题中,如何创设试题情境是一种智慧的挑 战。试题情境需要命题教师对教学本身进行周密思考与精心

设计,试题情境要学生在应试过程中自己去经历、体会、理 解,要有让学生思考的时间和空间,使学生在一个曾经历过 的熟悉的背景下,产生一种巨大的无形的导引效应,使自己 全身心投入到解决问题的数学化过程活动中,从自己的经验 出发,运用属于自己的方式和策略,寻找解决问题的方法, 发现和整理属于自己的不同形式的解题策略,经历数学化的 过程。 例2:(南京市): 问题情境 已知矩形的面积为a(a为常数,a>0),当该矩形的长 为多少时,它的周长最小?最小值是多少? 数学模型 设该矩形的长为x,周长为”,则y与x的函数关系式为 y=2(x+9)(>0) 探索研究 (1我们可以借鉴以前研究函数的经验,先探索函数 y=x+之0的图象性质
设计,试题情境要学生在应试过程中自己去经历、体会、理 解,要有让学生思考的时间和空间,使学生在一个曾经历过 的熟悉的背景下,产生一种巨大的无形的导引效应,使自己 全身心投入到解决问题的数学化过程活动中,从自己的经验 出发,运用属于自己的方式和策略,寻找解决问题的方法, 发现和整理属于自己的不同形式的解题策略,经历数学化的 过程。 例 2:(南京市): 问题情境 已知矩形的面积为 ( 为常数, ),当该矩形的长 为多少时,它的周长最小?最小值是多少? 数学模型 设该矩形的长为 ,周长为 ,则 与 的函数关系式为 。 探索研究 ⑴我们可以借鉴以前研究函数的经验,先探索函数 的图象性质

时宁 图2-1 ①填写下表,在图2一1中画出函数的图象: x .}123 4. . ②观察图象,写出该函数两条不同类型的性质; ③在求二次函数y=ax+x+a≠0的最大(小)值时,除了 通过观察图象,还可以通过配方得到.请你通过配方求函数 y=x+>0)的最小值 解决问题 (2)用上述方法解决“问题情境”中的问题,直接写出答案。 解析:1①将表中:的值代入=+>0) 中计算可得y的值分别为:4,3,2,2,2,3,4。描 点并画出函数=+x>0的图象如图2一2所示
① 填写下表,在图 2—1 中画出函数的图象: . 1 2 3 4 . . . ② 观察图象,写出该函数两条不同类型的性质; ③在求二次函数 的最大(小)值时,除了 通过观察图象,还可以通过配方得到.请你通过配方求函数 的最小值 解决问题 ⑵用上述方法解决“问题情境”中的问题,直接写出答案。 解析:⑴①将表中 的值代入 中计算可得 的值分别为: , , ,2, , , 。描 点并画出函数 的图象如图 2—2 所示

竹芳苏 图2-2 ②本题答案不唯一。要根据图象,可得:当01时,y随x增大而增大;当x=1时函数 y=x+(x>0)的最小值为2等。 g-周-2+-月 当一=0即=1时,西数+c0的最小值为2, (2)当该矩形的长为时,它的周长最小,最小值为46】 赏析:本题首先提出一个具体的问题情境,即“已知矩 形的面积为a(a为常数,a>0),当该矩形的长为多少时, 它的周长最小?最小值是多少?”让学生借鉴已经掌握的研 究函数的经验,突出学科结合与高中内容的衔接,先探索函 数x+>0的图象性质,再解决“问题情境”中提出的问 题。其过程就是经历数学化的思维过程。试题注重创造“最 近发展区”,引发学生思考,让学生在思考中体验知识的 形成过程,让学生始终处于“思考—收获一再思考— 再收获”的这样一种情感体验之中。用睿智的语言加以点化
②本题答案不唯一。要根据图象,可得:当 时, 随 增大而减小;当 时, 随 增大而增大;当 时函数 的最小值为 2 等。 ③ 当 ,即 时,函数 的最小值为 2. ⑵当该矩形的长为 时,它的周长最小,最小值为 . 赏析:本题首先提出一个具体的问题情境,即“已知矩 形的面积为 ( 为常数, ),当该矩形的长为多少时, 它的周长最小?最小值是多少?”让学生借鉴已经掌握的研 究函数的经验,突出学科结合与高中内容的衔接,先探索函 数 的图象性质,再解决“问题情境”中提出的问 题。其过程就是经历数学化的思维过程。试题注重创造“最 近发展区” , 引发学生思考,让学生在思考中体验知识的 形成过程,让学生始终处于“思考——收获——再思考—— 再收获”的这样一种情感体验之中。用睿智的语言加以点化
突现评价的导向功能,从而激发和培养学生的数学化思考, 引领学生的思维往纵深发展,保证学生应试过程中在和谐融 洽的气氛中按既定目标顺利进行。 例3:(盐城) 情境观察: 将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△ A'CD,如图3一1所示,将△A'CD的顶点A与点A重合,并 绕点A按逆时针方向旋转,使点D、A(A)、B在同一条直线上 如图3一2所示。 观察图3一2可知:与C相等的线段是■ ,∠CAC'= 9 A A(A 图3一1 图3—2 问题探究 如图3一3,△ABC中,AG⊥BC于点C,以A为直角顶点, 分别以AB、AC为直角边,向△ABC外作等腰R△ABE和等腰R △ACP,过点E、F作射线GA的垂线,垂足分别为P、2.。 试探究P与F之间的数量关系,并证明你的结论。 拓展延伸
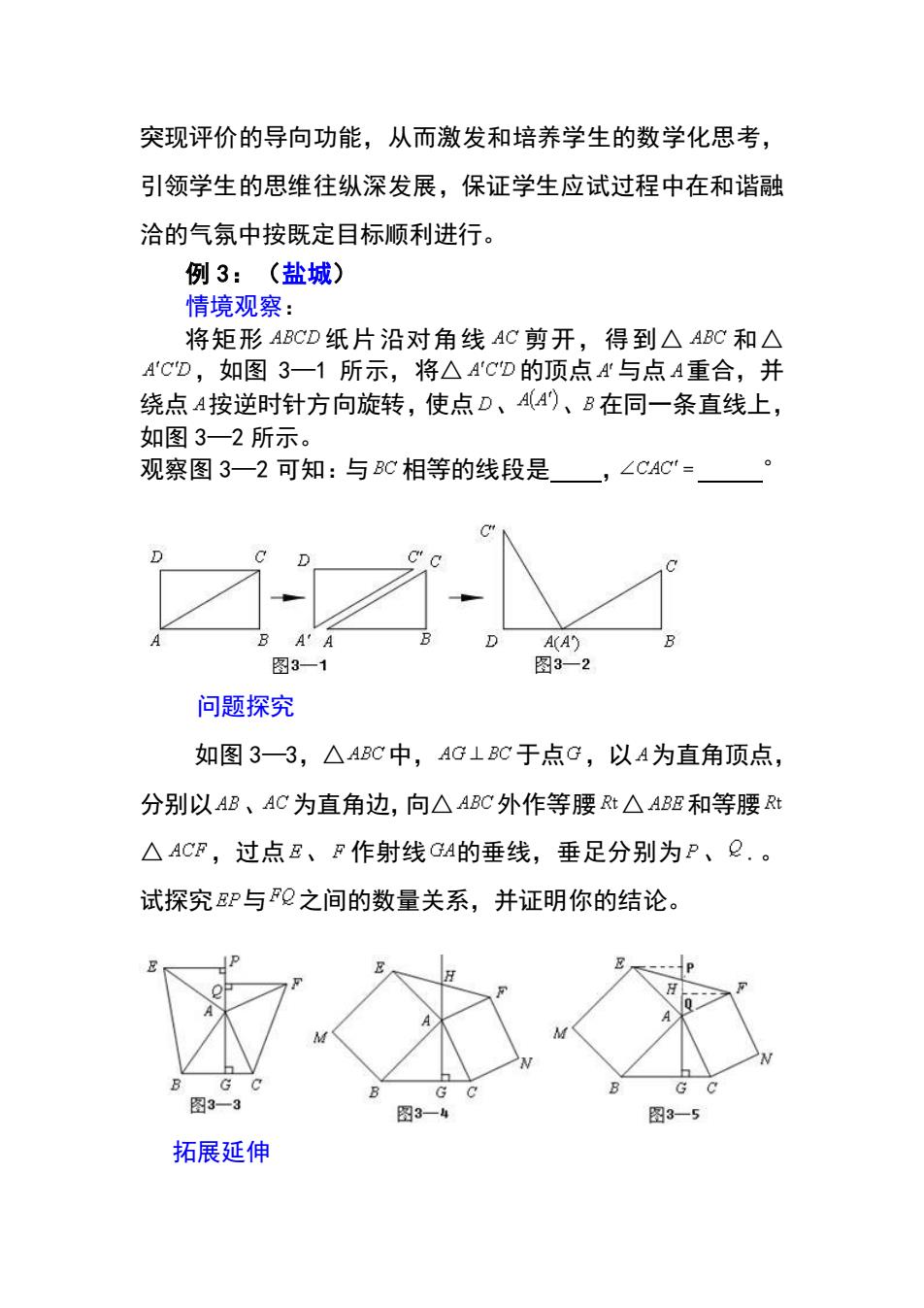
突现评价的导向功能,从而激发和培养学生的数学化思考, 引领学生的思维往纵深发展,保证学生应试过程中在和谐融 洽的气氛中按既定目标顺利进行。 例 3:(盐城) 情境观察: 将矩形 纸片沿对角线 剪开,得到△ 和△ ,如图 3—1 所示,将△ 的顶点 与点 重合,并 绕点 按逆时针方向旋转,使点 、 、 在同一条直线上, 如图 3—2 所示。 观察图 3—2 可知:与 相等的线段是 , ° 问题探究 如图 3—3,△ 中, 于点 ,以 为直角顶点, 分别以 、 为直角边,向△ 外作等腰 △ 和等腰 △ ,过点 、 作射线 的垂线,垂足分别为 、 .。 试探究 与 之间的数量关系,并证明你的结论。 拓展延伸

如图3一4,△ABC中,AG⊥BC于点G,分别以AB、AC为 一边向△ABC外作矩形ABMB和矩形ACNF,射线GA交EF于点 H。若AB=AB,AC=AF,试探究HE与HF之间的数量关系, 并说明理由。 解析:情境观察:易见与C相等的线段是AD,它们是矩 形的对边。∠CAC=180°-∠CAD-∠CAB=180°-90°=90°。 问题探究:找一个可能与P和都相等的线段AG。考 虑△ABG≌△EAP,这用SAS易证,得出AG=EP。同样考 虑&△ACG≌形△FA9,得出4G=2,从而得证。 拓展延伸:如图3-5,过点E作P⊥GA,21GA,垂足 分别为P、口。与问题探究相仿,只不过将全等改为相似, 证出EP=FQ,再证形△PH≌△PQH,从而得证。 赏析:本题是研究性学习问题,在问题设计上层层深入, 每一步都为下一步的思维活动打下基础,是一个蕴涵了让学 生经历观察、猜测、合情推理、有条理论证的数学化思维过 程,考查了基于数学实验的数学问题形成的一般思路及探究 能力。 3.回归教育本原、贴近学生数学化发展需求 陶行知先生曾说过:“教育必须做到解放学生的眼晴, 让他们亲自看一看;解放学生的大脑,让他们亲自想一想; 解放学生的嘴巴,让他们亲自说一说;解放学生的双手,让 他们亲自做一做。”我们认为,这是对素质教育的最佳诠释
如图 3—4,△ 中, 于点 ,分别以 、 为 一边向△ 外作矩形 和矩形 ,射线 交 于点 。若 , ,试探究 与 之间的数量关系, 并说明理由。 解析:情境观察:易见与 相等的线段是 ,它们是矩 形的对边。 。 问题探究:找一个可能与 和 都相等的线段 。考 虑 △ ≌ △ ,这用 易证,得出 。同样考 虑 △ ≌ △ ,得出 ,从而得证。 拓展延伸:如图 3—5,过点 作 , ,垂足 分别为 、 。与问题探究相仿,只不过将全等改为相似, 证出 EP FQ = ,再证 △ ≌ △ ,从而得证。 赏析:本题是研究性学习问题,在问题设计上层层深入, 每一步都为下一步的思维活动打下基础,是一个蕴涵了让学 生经历观察、猜测、合情推理、有条理论证的数学化思维过 程,考查了基于数学实验的数学问题形成的一般思路及探究 能力。 3.回归教育本原、贴近学生数学化发展需求 陶行知先生曾说过:“教育必须做到解放学生的眼睛, 让他们亲自看一看;解放学生的大脑,让他们亲自想一想; 解放学生的嘴巴,让他们亲自说一说;解放学生的双手,让 他们亲自做一做。”我们认为,这是对素质教育的最佳诠释

回归教育本原、贴近学生数学化发展需求,是全面实施数学 素质教育的根本所在。中考命题中如何从具体情境中抽象出 数学材料,并将获得的材料符号化,体现了数学问题源于教 学但高于教学的教学理念,使试题始终散发着“数学味”, 促进学生个性的充分发展一直是各地命题专家关注的热点。 例4(北京):阅读下面材料: 小伟遇到这样一个问题,如图4一1,在梯形ABCD中, AD∥BC,对角线AC,BD相交于点O。若梯形ABCD的面积为 1,试求以AC,BD,AD+BC的长度为三边长的三角形的面积 图4一1 图4一 小伟是这样思考的:要想解决这个问题,首先应想办法 移动这些分散的线段,构造一个三角形,再计算其面积即可。 他先后尝试了翻折,旋转,平移的方法,发现通过平移可以 解决这个问题。他的方法是过点D作AC的平行线交BC的延 长线于点E,得到的△BDE即是以AC,BD,AD+BC的长度为 三边长的三角形(如图4一2)。 参考小伟同学的思考问题的方法,解决下列问题: 如图4一3,△ABC的三条中线分别为AD,BE,GF
回归教育本原、贴近学生数学化发展需求,是全面实施数学 素质教育的根本所在。中考命题中如何从具体情境中抽象出 数学材料,并将获得的材料符号化,体现了数学问题源于教 学但高于教学的教学理念,使试题始终散发着“数学味” , 促进学生个性的充分发展一直是各地命题专家关注的热点。 例 4(北京):阅读下面材料: 小伟遇到这样一个问题,如图 4—1,在梯形 ABCD 中, AD∥BC,对角线 AC,BD 相交于点 O。若梯形 ABCD 的面积为 1,试求以 AC,BD, 的长度为三边长的三角形的面积。 小伟是这样思考的:要想解决这个问题,首先应想办法 移动这些分散的线段,构造一个三角形,再计算其面积即可。 他先后尝试了翻折,旋转,平移的方法,发现通过平移可以 解决这个问题。他的方法是过点 D 作 AC 的平行线交 BC 的延 长线于点 E,得到的△BDE 即是以 AC,BD, 的长度为 三边长的三角形(如图 4—2)。 参考小伟同学的思考问题的方法,解决下列问题: 如图 4—3,△ABC 的三条中线分别为 AD,BE,CF

(1)在图3中利用图形变换画出并指明以AD,BE,CF的长 度为三边长的一个三角形(保留画图痕迹); (2若△ABC的面积为1,则以AD,BE,CF的长度为三边长 的三角形的面积等于 图4-5 解析:(1)本题画法很多,答案不唯一。如: 方法一:如图4一4,过A作BC的平行线与过C作AD的平 行线相交于点P,则△FPC为所求。 方法二:如图4一5,延长AD至P,使DP=DA,取BP的中点 G。△FGC为所求; 2如图45,由已知易得n-8,要求△G℃的面积, 需要证△FGC的面积等于四边形FEBC面积。由(1)知四边形 BGCE是平行四边形,设FC与BE交于M,AD与BE交于N,则 MA8w2.有=8ame=m,8ae=8《侗底C
⑴在图 3 中利用图形变换画出并指明以 AD,BE,CF 的长 度为三边长的一个三角形(保留画图痕迹); ⑵若△ABC 的面积为 1,则以 AD,BE,CF 的长度为三边长 的三角形的面积等于_。 解析:⑴本题画法很多,答案不唯一。如: 方法一:如图 4—4,过 作 的平行线与过 作 的平 行线相交于点 ,则△ 为所求。 方法二:如图 4—5,延长 至 ,使 ,取 的中点 。△ 为所求; ⑵如图 4—5,由已知易得 ,要求△ 的面积, 需要证△ 的面积等于四边形 面积。由⑴知四边形 是平行四边形,设 与 交于 , 与 交于 ,则 ,有 , (同底

且等高)。两式相加可得结果。本题图形的本质特征是:以 三角形三条中线为边的三角形面积是原三角形面积的4。 例5:(绍兴)数学课上,李老师出示了如下题目。 在等边三角形ABC中,点E在AB上,点D在CB的延长线 上,且D=EC,如图5一1,试确定线段AB与DB的大小关系, 并说明理由。 小敏与同桌小聪讨论后,进行了如下解答: (1)特殊情况,探索结论 当点E为AB的中点时,如图5一1,确定线段AE与DB的 大小关系,请你直接写出结论: AEDB(填“>”,“” “<”或“=”).理由如下:如图5一2,过点E作F1/BC, 交AC于点F。(请你完成以下解答过程) (3)拓展结论,设计新题
且等高)。两式相加可得结果。本题图形的本质特征是:以 三角形三条中线为边的三角形面积是原三角形面积的 。 例 5: (绍兴)数学课上,李老师出示了如下题目。 在等边三角形 中,点 在 上,点 在 的延长线 上,且 ,如图 5—1,试确定线段 与 的大小关系, 并说明理由。 小敏与同桌小聪讨论后,进行了如下解答: ⑴特殊情况,探索结论 当点 为 的中点时,如图 5—1,确定线段 与 的 大小关系,请你直接写出结论: (填“>”,“”, “<”或“=”).理由如下:如图 5—2,过点 作 , 交 于点 。(请你完成以下解答过程) ⑶拓展结论,设计新题