
数学教育简史 与 中国数学教育的国际地位及文化背景 主讲教师:xi ehm
主讲教师:xiehm 数学教育简史 与 中国数学教育的国际地位及文化背景

这门课程自"文革"结束,一直称"中学数学教 材教法";1994年,国家教育委员会颁发了《普通 高等师范学校数学教育专业(本科)教育教学基本 要求(试行)》,为贯彻落实基本要求,将"中学 数学教材教法"课程定名为"数学教育学",以适应 学科发展.1998年,教育部颁布高等学校专业目录 把"数学教学论"作为数学与应用数学(师范类)专 业的主要课程之一,数学教育学研究的对象是数 学教学论,数学学习论和数学课程论等.考虑到 学科的发展与课程的建设,该课程仍继续称"数学 教育学",在进行教学过程中,重点讲述"数学教 学论",同时兼顾"数学学习论"和"数学课程论"的 学习.保持"数学教育学"的体系结构,以利课程 建设
这门课程自"文革"结束,一直称"中学数学教 材教法" ;1994年,国家教育委员会颁发了《普通 高等师范学校数学教育专业(本科)教育教学基本 要求(试行)》,为贯彻落实基本要求,将"中学 数学教材教法"课程定名为"数学教育学",以适应 学科发展.1998年,教育部颁布高等学校专业目录, 把"数学教学论"作为数学与应用数学(师范类)专 业的主要课程之一.数学教育学研究的对象是数 学教学论,数学学习论和数学课程论等.考虑到 学科的发展与课程的建设,该课程仍继续称"数学 教育学" ,在进行教学过程中,重点讲述"数学教 学论",同时兼顾"数学学习论"和"数学课程论"的 学习.保持"数学教育学"的体系结构,以利课程 建设.

第一节 数学教育的国际比较 在中学的众多课程里,数学是最具国际比较 性的学科,世界各国的中小学数学课程内容大同 小异。从1980年以来,国际性的中小学数学成绩 测试一直在进行,许多国家把这些成绩作为国家 教育水平的衡衡量标志。 美国和前苏联是当今世界上数学水平最高的 国家,欧洲紧随其后,日本正在迎头赶上。中国 现代数学的发展已经引起世人注意,但还没有成 为“世界数学大国”。 国际数学教育成就评价(IAEP)数学和科学成绩 平均正确率(依13岁学生数学成绩排列1989年公布):
第一节 数学教育的国际比较 在中学的众多课程里,数学是最具国际比较 性的学科,世界各国的中小学数学课程内容大同 小异。从1980年以来,国际性的中小学数学成绩 测试一直在进行,许多国家把这些成绩作为国家 教育水平的衡量标志。 美国和前苏联是当今世界上数学水平最高的 国家,欧洲紧随其后,日本正在迎头赶上。中国 现代数学的发展已经引起世人注意,但还没有成 为“世界数学大国”。 国际数学教育成就评价(I A E P)数学和科学成绩 平均正确率(依13岁学生数学成绩排列1989年公布):
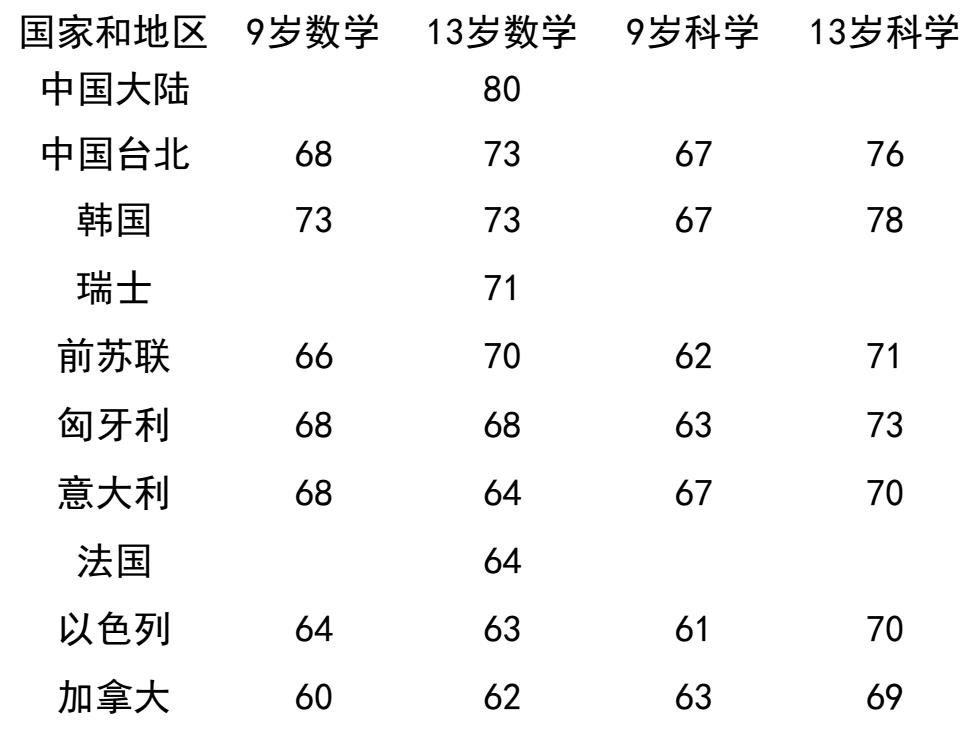
国家和地区 9岁数学 13岁数学 9岁科学 13岁科学 中国大陆 80 中国台北 68 73 67 76 韩国 73 73 67 78 瑞士 71 前苏联 66 70 62 71 匈牙利 68 68 63 73 意大利 68 64 67 70 法国 64 以色列 64 63 61 70 加拿大 60 62 63 69
国家和地区 9岁数学 13岁数学 9岁科学 13岁科学 中国大陆 80 中国台北 68 73 67 76 韩国 73 73 67 78 瑞士 71 前苏联 66 70 62 71 匈牙利 68 68 63 73 意大利 68 64 67 70 法国 64 以色列 64 63 61 70 加拿大 60 62 63 69
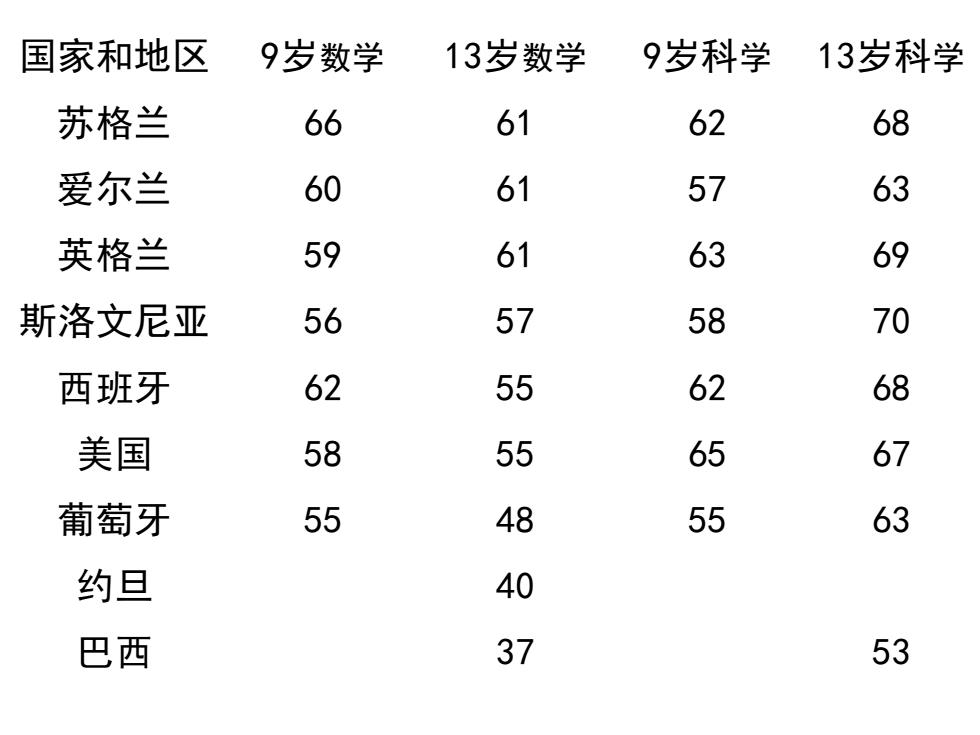
国家和地区 9岁数学 13岁数学 9岁科学 13岁科学 苏格兰 66 61 62 68 爱尔兰 60 61 57 63 英格兰 59 61 63 69 斯洛文尼亚 56 57 58 70 西班牙 62 55 62 68 美国 58 55 65 67 葡萄牙 55 48 55 63 约旦 40 巴西 37 53
国家和地区 9岁数学 13岁数学 9岁科学 13岁科学 苏格兰 66 61 62 68 爱尔兰 60 61 57 63 英格兰 59 61 63 69 斯洛文尼亚 56 57 58 70 西班牙 62 55 62 68 美国 58 55 65 67 葡萄牙 55 48 55 63 约旦 40 巴西 37 53

第二节中国传统文化对数学教育的影响 一、儒家文化的教育传统 儒家文化的教育特征,可以概括为“苦读+考 试”。读书的目的是博取功名。这种传统至今对数 学教育有重大影响。具体说来有: *儒家文化鼓励读书人“为今生今世建功立业 而奋斗”,读书目的明确。 *家庭的严格管束。 *传统教育强调背诵、模仿记忆、“熟能生 巧”。 大运动量的“数学练习”是考试成功的基 础。 *中国古代数学的“计算”传统。(如计算口 快姐姐上口庙王记忆笔)
第二节 中国传统文化对数学教育的影响 一 、儒家文化的教育传统 儒家文化的教育特征,可以概括为“苦读+考 试”。读书的目的是博取功名。这种传统至今对数 学教育有重大影响。具体说来有: *儒家文化鼓励读书人“为今生今世建功立业 而奋斗”,读书目的明确。 *家庭的严格管束。 *传统教育强调背诵、模仿记忆、“熟能生 巧”。大运动量的“数学练习”是考试成功的基 础。 *中国古代数学的“计算”传统。(如计算口 诀朗朗上口,便于记忆等)

二 儒家文化本身的演绎特征 儒家文化本身是一个演绎系统。作如下类比: 儒家经典相当于数学的公理,朱熹等为经典作 注引申是构作定理和论证,读书人的任务是按朱熹 的标准答案做练习。 儒家文化的思想体系,从表面上看似乎不讲究 逻辑推理和演绎论证,但就整体来看,思维方式是 收敛的、封闭的、演绎的。 儒家文化是一种注释文化。学者只能为圣人的 话做“注解”,自己的学术研究都是为了证明“圣 人”的话是对的。这种思想体系不可避免地渗入中 国知识分子的血液之中,在思想深处压抑着创造性 包括数学的创新精神
二、儒家文化本身的演绎特征 儒家文化本身是一个演绎系统。作如下类比: 儒家经典相当于数学的公理,朱熹等为经典作 注引申是构作定理和论证,读书人的任务是按朱熹 的标准答案做练习。 儒家文化的思想体系,从表面上看似乎不讲究 逻辑推理和演绎论证,但就整体来看,思维方式是 收敛的、封闭的、演绎的。 儒家文化是一种注释文化。学者只能为圣人的 话做“注解”,自己的学术研究都是为了证明“圣 人”的话是对的。这种思想体系不可避免地渗入中 国知识分子的血液之中,在思想深处压抑着创造性, 包括数学的创新精神

三、清代儒家“考据文化”为数学的逻辑推 理提供了舞台 戴震(1723一1777)为代表的考据学派,以慎 重求证的治学态度,极力反对空泛而粗放的论证方 法。他曾批评以前的治学方法是:“依于传闻,以 拟其是;择于众说,以裁其优;出于空言,以定其 论;据于孤证,以信其通” 。 考据训练=科学精神,数学思想=逻辑方法 考据文化使数学教育“重证据、讲推理”的特 点得到充分发挥。中国知识分子的“考据文化”传 统,把西方数学中的“创新”层面“过滤掉”,只 把“逻辑”层面留下,以至于“数学=逻辑”的观 念得到普遍认可,而数学的创新则不可避免地被冷
三、清代儒家“考据文化”为数学的逻辑推 理提供了舞台 戴震(1723—1777)为代表的考据学派,以慎 重求证的治学态度,极力反对空泛而粗放的论证方 法。他曾批评以前的治学方法是:“依于传闻,以 拟其是;择于众说,以裁其优;出于空言,以定其 论;据于孤证,以信其通” 。 考据训练=科学精神,数学思想=逻辑方法 考据文化使数学教育“重证据、讲推理”的特 点得到充分发挥。中国知识分子的“考据文化”传 统,把西方数学中的“创新”层面“过滤掉”,只 把“逻辑”层面留下,以至于“数学=逻辑”的观 念得到普遍认可,而数学的创新则不可避免地被冷 落了

四、儒家的“科举考试制度”形成了考试文 化考试作为教育的指挥棒,古今中外都一样, 但在中国更为突出。自隋文帝于公元587年实行 科举制度以来,通过考试博取功名成为知识分子 的唯一目标。 1935年爱因斯坦在纽约州立大学的毕业典礼 上,指出旧学校给学生太多的“好胜心”,而不 注意培养学生的“好奇心”。李政道在演讲时说 过,我们的传统把学习称作“学问”,为什么你 们老是在做“学答”? 实际上,考试是一把双刃剑
四、儒家的“科举考试制度”形成了考试文 化 考试作为教育的指挥棒,古今中外都一样, 但在中国更为突出。自隋文帝于公元587年实行 科举制度以来,通过考试博取功名成为知识分子 的唯一目标。 1935年爱因斯坦在纽约州立大学的毕业典礼 上,指出旧学校给学生太多的“好胜心”,而不 注意培养学生的“好奇心”。李政道在演讲时说 过,我们的传统把学习称作“学问”,为什么你 们老是在做“学答”? 实际上,考试是一把双刃剑

第三节 国际数学教育百年回顾 近代数学教育改革的首创者培利,他提倡 “实用数学”,设置“数学实验室”。他指出 “那种抽象的算教育,百人中仅有五人成功”, 而“我们没有像欧几里德时代那样多的空间和时 间了。”培利的数学教育改革打破了在数学教育 中欧氏几何一统天下的格局,并使许多新内容如 圆锥曲线、微积分等进入了中等数学教育。他的 改革对全世界的数学教育产生了积极影响。 1901年他抨击英国的教育制度,反对“为培 养一个数学家而毁灭数以百万人的数学精神”。 他归纳学习数学的“理由”有七条:
第三节 国际数学教育百年回顾 近代数学教育改革的首创者培利,他提倡 “实用数学”,设置“数学实验室” 。他指出 “那种抽象的算教育,百人中仅有五人成功” , 而“我们没有像欧几里德时代那样多的空间和时 间了。”培利的数学教育改革打破了在数学教育 中欧氏几何一统天下的格局,并使许多新内容如 圆锥曲线、微积分等进入了中等数学教育。他的 改革对全世界的数学教育产生了积极影响。 1901年他抨击英国的教育制度,反对“为培 养一个数学家而毁灭数以百万人的数学精神” 。 他归纳学习数学的“理由”有七条: