
中学数学逻辑基础 ·数学概念 ·数学命题 。数学证明 2024/8/17 1
2024/8/17 1 中学数学逻辑基础 • 数学概念 • 数学命题 • 数学证明

1、数学概念 1、概念和数学概念 ¤概念是反映事物本质属性的思维形式,而数学概念自然就是 反映现实世界空间形式和数量关系本质属性的思维形式。例如 圆,本质属性:平面内到定点的距离等于定长的点的集合,非 本质属性:半径的长短。平行四边形:“两组对边分别平 行”“四条边” ¤正确的概念是科学抽象的结果:去掉事物次要的方面,得到了 事物的本质属性。如数、形。 ¤数学概念的形成的途径是多样的:从现实模型直接得出;经过 多级抽象得出;把客观事物理想化和纯粹化得出;为了数学的 需要从数学内部产生;根据有理论上存在的可能性而提出等。 2024/8/17 2
2024/8/17 2 1、数学概念 1、概念和数学概念 ¤ 概念是反映事物本质属性的思维形式,而数学概念自然就是 反映现实世界空间形式和数量关系本质属性的思维形式。例如 圆,本质属性:平面内到定点的距离等于定长的点的集合,非 本质属性:半径的长短。平行四边形:“两组对边分别平 行”“四条边” ¤ 正确的概念是科学抽象的结果:去掉事物次要的方面,得到了 事物的本质属性。如数、形。 ¤ 数学概念的形成的途径是多样的:从现实模型直接得出;经过 多级抽象得出;把客观事物理想化和纯粹化得出;为了数学的 需要从数学内部产生;根据有理论上存在的可能性而提出等

¤数学概念是发展变化的:原因一方面事物是发展变化 的,另一方面人们的认识是不断深化的。如:自然数 集(加零)→扩大的自然数集(加正分数)→算术数 集(加负整(分)数)→有理数集(加无理数)→实 数集(加虚数)→复数集 ¤概念和词语密切联系:语词是概念的语言形式,而概 念是语词的思想内容,两者密切联系,不可分割。概 念和语词之间是一一对应的吗? ¤数学概念的重要性:非常基本,也非常重要,判断由 概念构成,推理由判断构成,论证由判断和推理构成, 因此概念是其他思维形式的基础,是思维的细胞。 2024/8/17 3
2024/8/17 3 ¤ 数学概念是发展变化的:原因一方面事物是发展变化 的,另一方面人们的认识是不断深化的。如:自然数 集(加零)→扩大的自然数集(加正分数)→算术数 集(加负整(分)数)→有理数集(加无理数)→实 数集(加虚数)→复数集 ¤ 概念和词语密切联系:语词是概念的语言形式,而概 念是语词的思想内容,两者密切联系,不可分割。概 念和语词之间是一一对应的吗? ¤ 数学概念的重要性:非常基本,也非常重要,判断由 概念构成,推理由判断构成,论证由判断和推理构成, 因此概念是其他思维形式的基础,是思维的细胞

2、概念的内涵和外延 ¤概念的内涵就是概念所反映的事物的本质属性的总和,是概念的 质的方面,它说明所反映的事物是什么样的。例如“矩形”概念 意味着有一个角为直角的平行四边形,这就是矩形的内涵。 ¤概念的外延就是概念所反映的事物的总和(或范围)。是概念的量 的方面,它说明概念所反映的是哪些事物。例如平行四边形这个 概念是指一般的平行四边形、矩形、菱形、正方形的全体,这就 是平行四边形这一概念的外延。 01 概念的内涵和外延关系密切、互相依赖。每一个(数学)概念都 既有明确的内涵又有确定的外延,因此概念之间是彼此互相区别 界限分明的。教学要求中的概念明确就是指既要明确其内涵又要 明确其外延。 2024/8/17 4
2024/8/17 4 2、概念的内涵和外延 ¤ 概念的内涵就是概念所反映的事物的本质属性的总和, 是概念的 质的方面,它说明所反映的事物是什么样的。例如“矩形”概念, 意味着有一个角为直角的平行四边形,这就是矩形的内涵。 ¤ 概念的外延就是概念所反映的事物的总和(或范围)。是概念的量 的方面,它说明概念所反映的是哪些事物。例如平行四边形这个 概念是指一般的平行四边形、矩形、菱形、正方形的全体,这就 是平行四边形这一概念的外延。 ¤ 概念的内涵和外延关系密切、互相依赖。每一个(数学)概念都 既有明确的内涵又有确定的外延,因此概念之间是彼此互相区别、 界限分明的。教学要求中的概念明确就是指既要明确其内涵又要 明确其外延
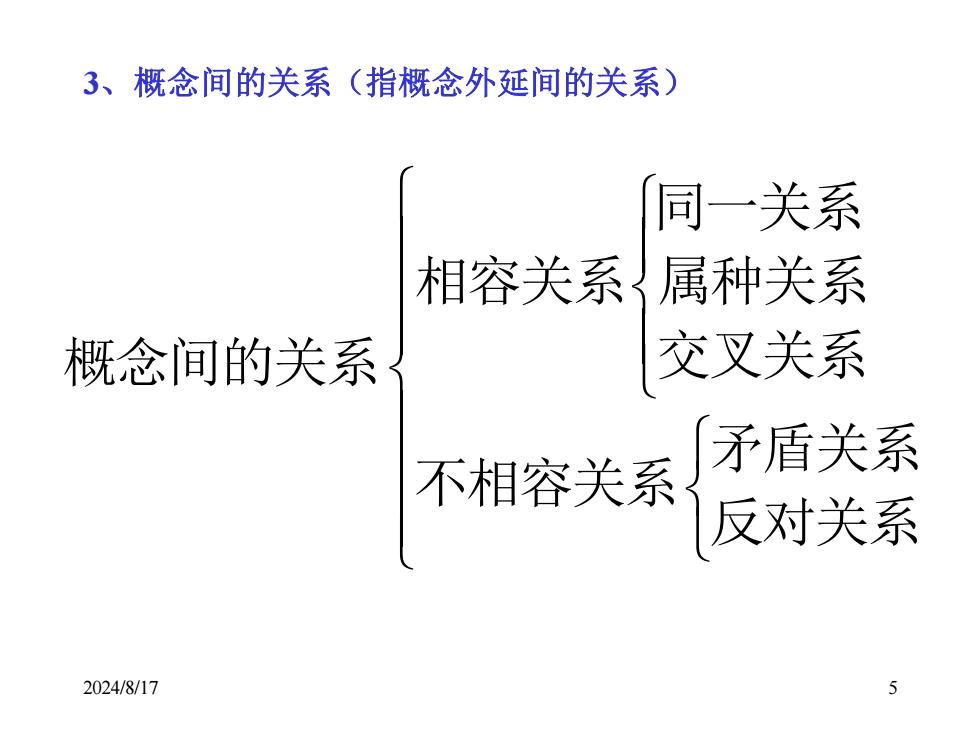
3、概念间的关系(指概念外延间的关系) 同一关系 相容关系属种关系 概念间的关系 交叉关系 不相容关系 矛盾关系 反对关系 2024/8/17 5
2024/8/17 5 3、概念间的关系(指概念外延间的关系) 反对关系 矛盾关系 不相容关系 交叉关系 属种关系 同一关系 相容关系 概念间的关系

·相容关系:两个概念外延之间至少有一部分重合。 ¤同一关系(全同关系):两个概念的外延完全重合, 如等腰三角形和等边三角形;最小的质数和最小的正 偶数;无理数和无限不循环小数等。 A B 2024/8/17 6
2024/8/17 6 • 相容关系:两个概念外延之间至少有一部分重合。 ¤ 同一关系(全同关系):两个概念的外延完全重合, 如等腰三角形和等边三角形;最小的质数和最小的正 偶数;无理数和无限不循环小数等。 A B
¤属种关系(从属关系):在两个概念之间,一个概念的外延完全 包含在另一个外延之中,而且仅仅成为另一个概念外延的一部分 例如四边形和平行四边形是具有属种关系的概念;实数和有理数 也具有属种关系的概念。在属种关系中,外延大的那个叫属概念 外延小的那个叫种概念(一个概念的属概念是否唯一,一个概念 的种概念是否唯一?) ¤注意:一是种类概念之间具有相对性。二是要区分从属关系和全 体与部分的关系。有的概念之间既有从属关系又有全体与部分的 关系。有的却不然。例如对数与它的直数、尾数之间的关系不 是从属关系只是全体与部分的关系。 B 2024/8/17 7
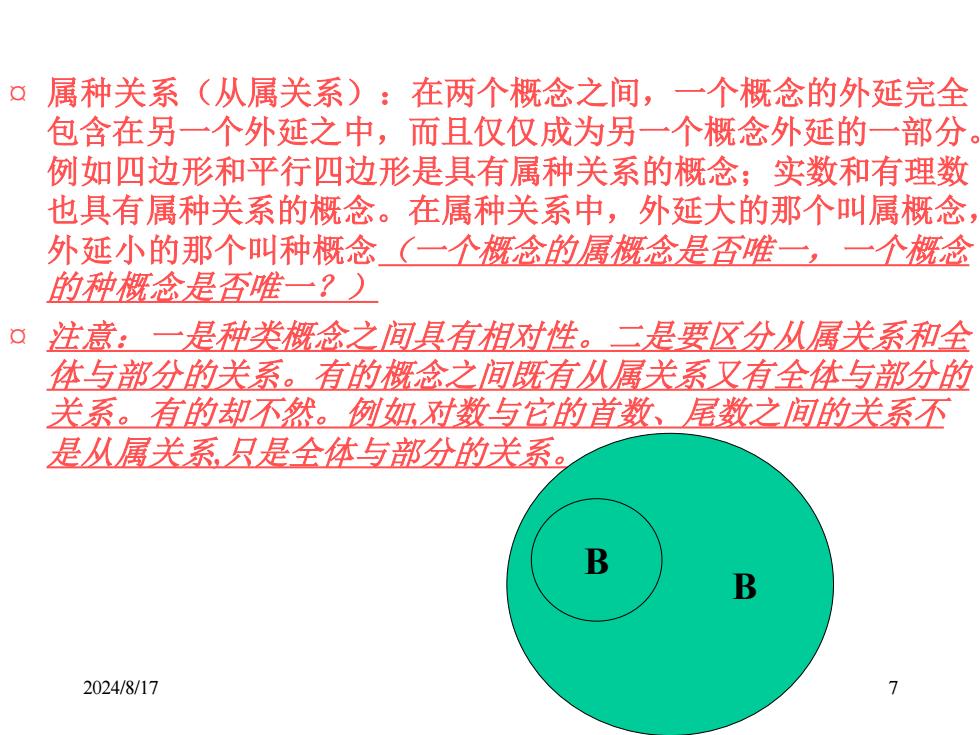
2024/8/17 7 ¤ 属种关系(从属关系):在两个概念之间,一个概念的外延完全 包含在另一个外延之中,而且仅仅成为另一个概念外延的一部分。 例如四边形和平行四边形是具有属种关系的概念;实数和有理数 也具有属种关系的概念。在属种关系中,外延大的那个叫属概念, 外延小的那个叫种概念(一个概念的属概念是否唯一,一个概念 的种概念是否唯一?) ¤ 注意:一是种类概念之间具有相对性。二是要区分从属关系和全 体与部分的关系。有的概念之间既有从属关系又有全体与部分的 关系。有的却不然。例如,对数与它的首数、尾数之间的关系不 是从属关系,只是全体与部分的关系。 A B B
¤交叉关系:两个概念的外延有而且只有一部分重合, 如菱形和矩形、等腰三角形和直角三角形、正数和整 数均为交差关系。 B 2024/8/17 8
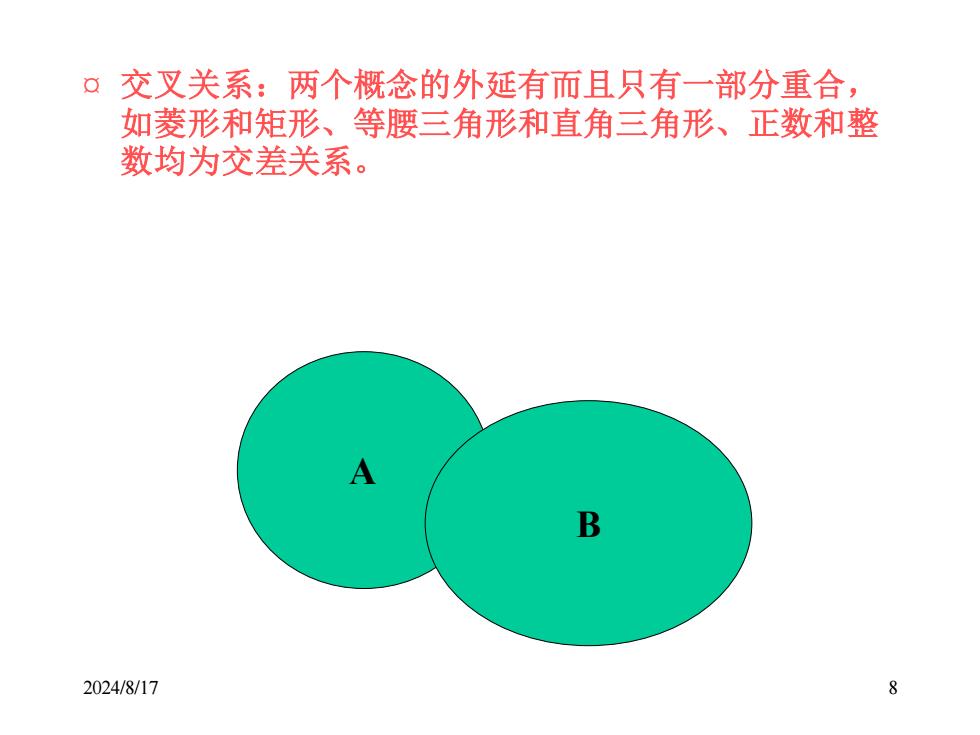
2024/8/17 8 ¤ 交叉关系:两个概念的外延有而且只有一部分重合, 如菱形和矩形、等腰三角形和直角三角形、正数和整 数均为交差关系。 A B
。j 不相容关系(全异关系):指属于一个属概念中的两 个在外延上没有任何重合部分的种概念之间的关系。 ¤矛盾关系:两个概念的外延完全不同,并且它们的外 延之和等于其属概念的外延。如有理数和无理数相对 于实数来说就是矛盾关系 A B 2024/8/17
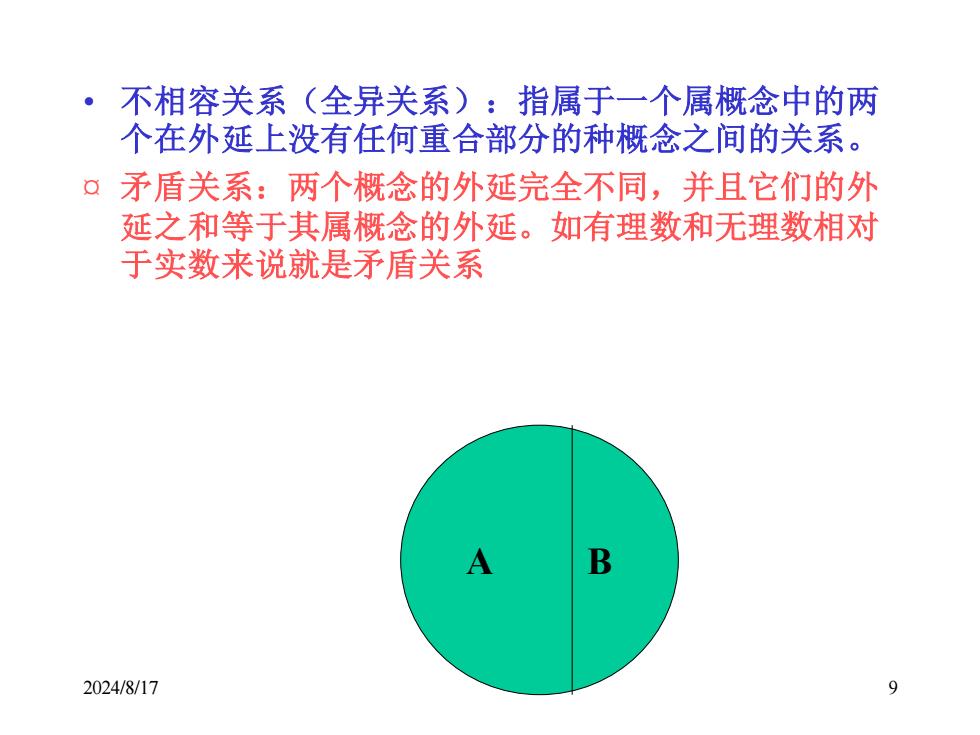
2024/8/17 9 • 不相容关系(全异关系):指属于一个属概念中的两 个在外延上没有任何重合部分的种概念之间的关系。 ¤ 矛盾关系:两个概念的外延完全不同,并且它们的外 延之和等于其属概念的外延。如有理数和无理数相对 于实数来说就是矛盾关系 A B
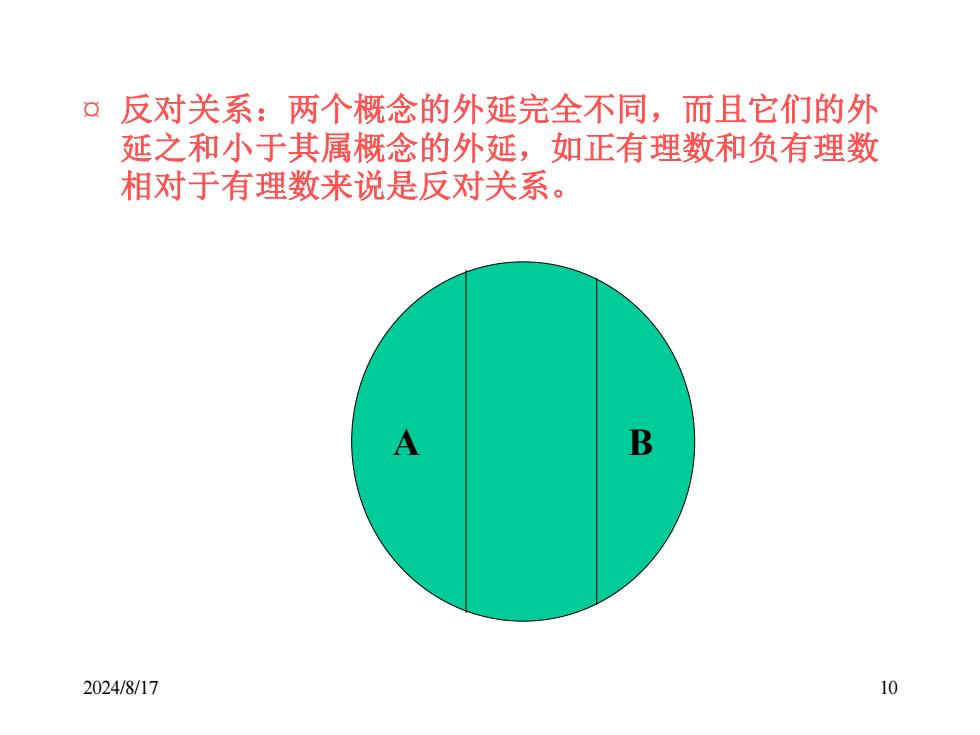
¤反对关系:两个概念的外延完全不同,而且它们的外 延之和小于其属概念的外延,如正有理数和负有理数 相对于有理数来说是反对关系。 A B 2024/8/17 10
2024/8/17 10 ¤ 反对关系:两个概念的外延完全不同,而且它们的外 延之和小于其属概念的外延,如正有理数和负有理数 相对于有理数来说是反对关系。 A B