
第二讲数学教学目标模型及制 定 §2.1教学目标分类 ■ §2.2数学教学目标模型 ■§2.3数学教学目标的制定
第二讲 数学教学目标模型及制 定 ◼ §2.1 教学目标分类 ◼ §2.2 数学教学目标模型 ◼ §2.3 数学教学目标的制定

§2.1教学目标分类 确定教学目标、实施教学活动、对教学效果进 行测量和评价构成教学过程中紧密联系的三个 主要环节。 ■教学目标是教学活动的依据,也是教学测量和 评价的依据。 ■当教学目标用于教学测量和评价时,教学目标 就转化为测量日标和评价日标。因此,教学目 标与测量和评价目标是一致的
§2.1 教学目标分类 ◼ 确定教学目标、实施教学活动、对教学效果进 行测量和评价构成教学过程中紧密联系的三个 主要环节。 ◼ 教学目标是教学活动的依据,也是教学测量和 评价的依据。 ◼ 当教学目标用于教学测量和评价时,教学目标 就转化为测量目标和评价目标。因此,教学目 标与测量和评价目标是一致的

、 教育目标分类 (一)涵义:用精确的术语详细地说明学生改 变其思维、感情和行为的方式就是教学目标 (B.S.Bloom)。 (二)表述:教学日标就是教师所预期的学生 在思维、情感和行动方面变化的数量和程度。 表述教学目标,就是以一种较特定的方式描述 在单元或学程完成之后,学生应能做(或产生) 些什么,或者学生应具备哪些特征。 教学目标的表述主要由内容和行为组成
一、教育目标分类 ◼ (一)涵义:用精确的术语详细地说明学生改 变其思维、感情和行为的方式就是教学目标 (B.S.Bloom)。 ◼ (二)表述:教学目标就是教师所预期的学生 在思维、情感和行动方面变化的数量和程度。 表述教学目标,就是以一种较特定的方式描述 在单元或学程完成之后,学生应能做(或产生) 些什么,或者学生应具备哪些特征。 ◼ 教学目标的表述主要由内容和行为组成

、教育目标分类 例:在“掌握二元一次方程组的解法” 这一教学目标中 ,“掌握”是行为目标 “二元一次方程组的解法”是目标的内 容 这是表述得当的教学目标应具有的两 个特征
一、教育目标分类 ◼ 例:在“掌握二元一次方程组的解法” 这一教学目标中 ◼ “掌握”是行为目标 ◼ “二元一次方程组的解法”是目标的内 容 ◼ ——这是表述得当的教学目标应具有的两 个特征

表述得当的教学目标要求: 1、表述应是学生学习的结果,而不是陈 述教师做什么; ■2、应力求明确具体,可以观察和测量, 忌用含糊的和不切实际的语言陈述目标; ■3、应反映学习结果的层次性: ■4、应能用来成功地向其他人表达或交流 教师的意图
表述得当的教学目标要求: ◼ 1、表述应是学生学习的结果,而不是陈 述教师做什么; ◼ 2、应力求明确具体,可以观察和测量, 忌用含糊的和不切实际的语言陈述目标; ◼ 3、应反映学习结果的层次性; ◼ 4、应能用来成功地向其他人表达或交流 教师的意图

例:理解一元二次方程的概念 理解”是内在心理的变化,不同的人 6“ 可能有不同的解释,也不易观察和测量。 可以列出其内在变化的行为样品: s i 能叙述一元二次方程的定义: ■能写出一元二次方程的一般形式: s i 能指出一元二次方程的肯定例证和否定 例证。(使目标变得十分具体清晰)
例:理解一元二次方程的概念 ◼ “理解”是内在心理的变化,不同的人 可能有不同的解释,也不易观察和测量。 可以列出其内在变化的行为样品: ◼ 能叙述一元二次方程的定义; ◼ 能写出一元二次方程的一般形式; ◼ 能指出一元二次方程的肯定例证和否定 例证。(使目标变得十分具体清晰)

(三)认知领域目标的分类 ·认知、情感、动作技能领域目标 ■认知领域的目标分类(Bloom): ·识记:对具体事物、处理方法和普遍原理的回忆 ·领会:抓住材料意义的一种能力(转化、解释) ·运用:概念、法则和原理的运用 ·分析:剖析要素、关系分析、结构原理 ■综合:把诸要素和部分组合在一起成为整体 ■评价:为特定目的对材料和方法的价值判断
(三)认知领域目标的分类 ◼ 认知、情感、动作技能领域目标 ◼ 认知领域的目标分类(Bloom): ◼ 识记:对具体事物、处理方法和普遍原理的回忆 ◼ 领会:抓住材料意义的一种能力(转化、解释) ◼ 运用:概念、法则和原理的运用 ◼ 分析:剖析要素、关系分析、结构原理 ◼ 综合:把诸要素和部分组合在一起成为整体 ◼ 评价:为特定目的对材料和方法的价值判断
认知领域教育目标分类 目标 层次 子层次 识记 术语和具体事实;处理事实方法的知识; 概括和结构的知识 领会 转述(化); 解释;知识用于具体情景 认知领域 运用 直接应用;见接应用 分析 要素分析;关系分析;组织结构分析 综合 形成观点和意见;拟订计划和方案;抽 象关系和理论 评价 依内部原理判断;依外在条件判断(新)
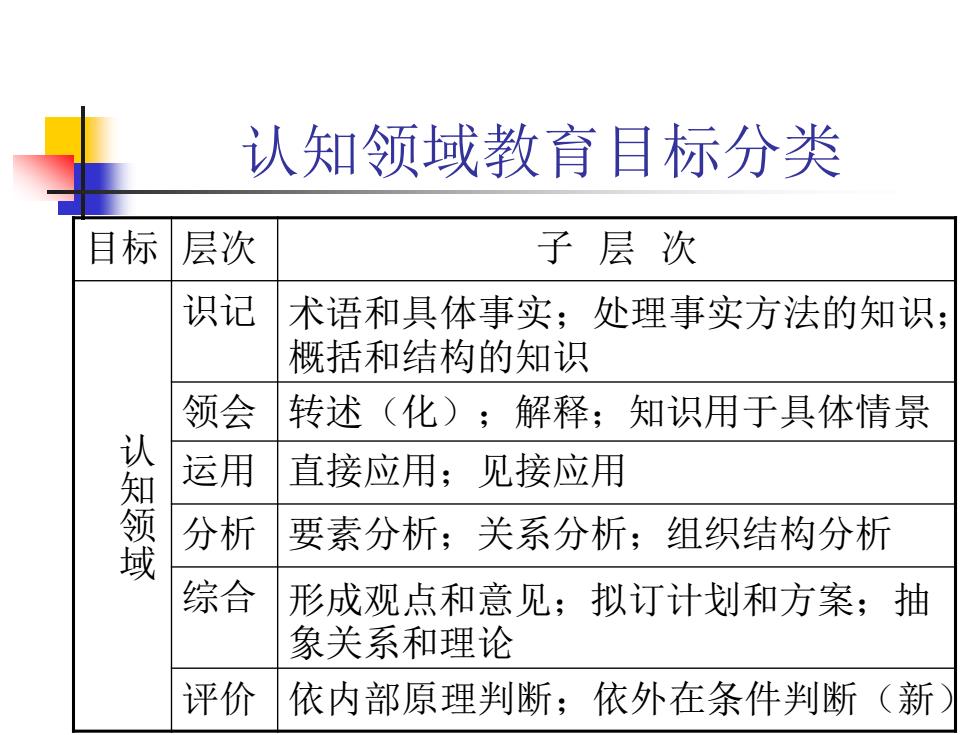
认知领域教育目标分类 目标 层次 子 层 次 认 知 领 域 识记 术语和具体事实;处理事实方法的知识; 概括和结构的知识 领会 转述(化);解释;知识用于具体情景 运用 直接应用;见接应用 分析 要素分析;关系分析;组织结构分析 综合 形成观点和意见;拟订计划和方案;抽 象关系和理论 评价 依内部原理判断;依外在条件判断(新)

例子: ■1.若x>0,y>0,求证: (x2+y2)1/2>(x3+y3)1/3。 ■2.证明:Kepler方程 X=q'sinx+a(0<q<1,a∈R)有唯一实根。 ■3.证明Ptolemy定理:圆内接四边形对边 乘积的和等于对角线的乘积。即 ABCD+AC.BD=ACBD ·对“分析水平”的分类是相当有意义的
例子: ◼ 1.若x>0,y>0,求证: (x 2 +y2 ) 1/2> (x 3 +y3 ) 1/3。 ◼ 2.证明:Kepler方程 x=q·sinx+a ( 0<q<1, aR)有唯一实根。 ◼ 3.证明Ptolemy定理:圆内接四边形对边 乘积的和等于对角线的乘积。即 AB·CD+AC·BD=AC·BD ◼ 对“分析水平”的分类是相当有意义的

(四)情感领域的目标分类 ■1、接受:感觉;愿意接受;控制和选择 ■2、反应:默许;愿意;满意的反应 ■3、赋予价值(态度):认可;喜爱;稳 固价值 ■4、组织价值:对立价值概念;组织价值 体系 ■5、形成品格:一般定向;形成品格
(四)情感领域的目标分类 ◼ 1、接受:感觉;愿意接受;控制和选择 ◼ 2、反应:默许;愿意;满意的反应 ◼ 3、赋予价值(态度):认可;喜爱;稳 固价值 ◼ 4、组织价值:对立价值概念;组织价值 体系 ◼ 5、形成品格:一般定向;形成品格