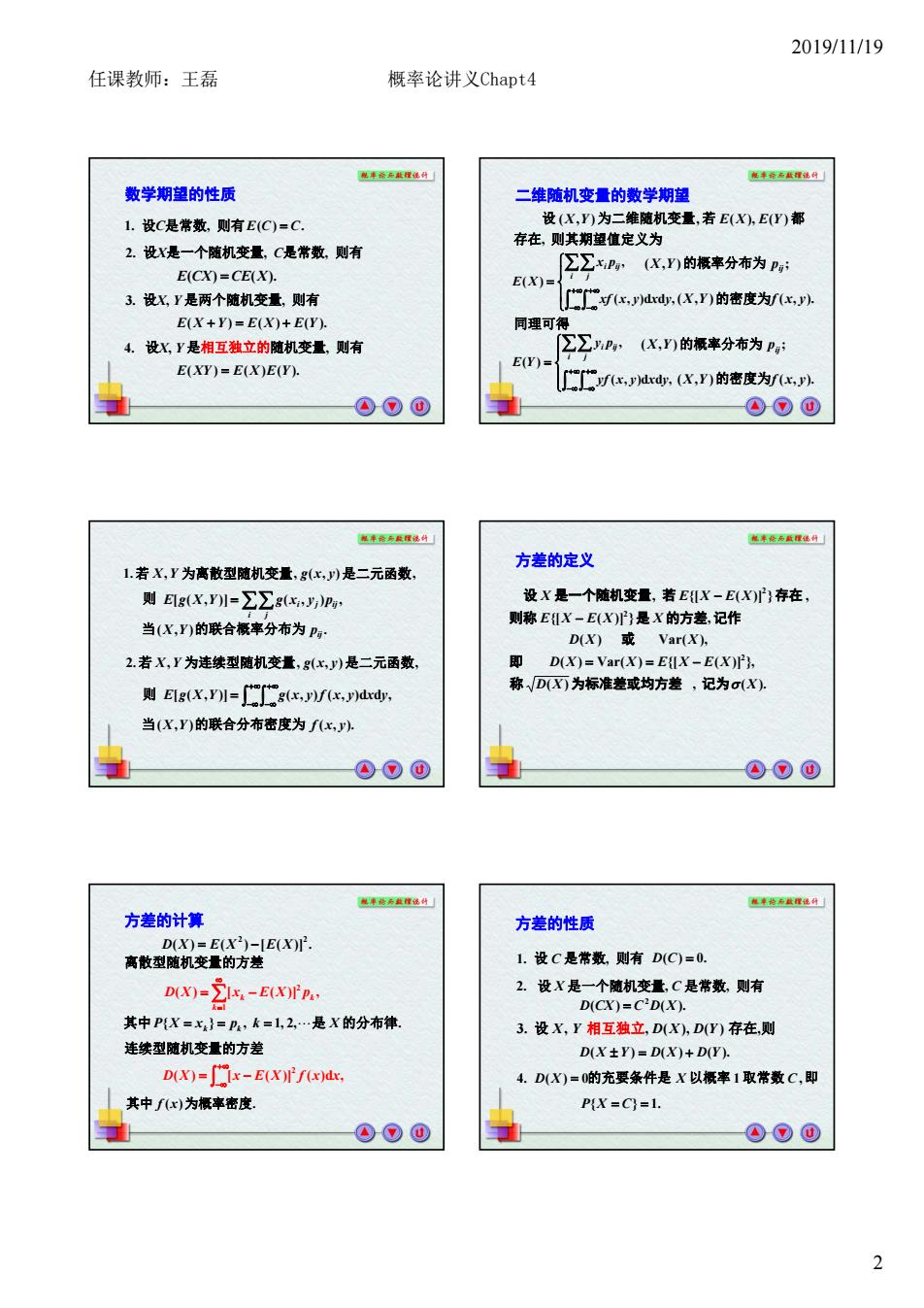
2019/11/19 任课教师：王磊 概率论讲义Chapt4 数学期望的性质 盖A 二维随机变量的数学期望 1.设C是常数，则有E(C)=C. 定义为 变量，若EX,E)都 2.设X是一个随机变量，C是常数则有 存在 CxPg,(X,Y)的概率分布为Py: E(CX)=CE(X). 3.设X了是两个随机变量，则有 x,dd,(X,Y)的密度为xJ以 E(X+)=E(X)+ET), 同建可得 设Xy是相互独立的随机变量，则有 ∑∑P,(X,)的橛率分布为P, E(XY)=E(X)E(Y) E(Y)- 工fx,dd,(X,y)的密度为xJ 方差的定义 1.若X,Y为离散型随机变量，g(x,)是二元函数 则Eg(X,1=∑∑g(x,p, 当(K,)的联合展率分布为P, -E(X) D(X 是X的方记作 Var(X) 2若X,Y为连续型随机变量，gx,)是二元函数 即称 则EgX,-g,/x,d ,记为() 当X,y)的联合分布密度为x,J ④⊙@ ⊙⊙0 方差的计算 方差的性质 青教 1.设C是常最，则有D(C=0. D(X)--E(X 2.设X是 个随机变量，C是常数，则有 DCX)■CDX 其中PX=x=p,k=l,2…是X的分布钟 3.设X,y相互独立，D(X.DW)存在，则 连续型随机变量的方差 D(X±)■DX)+DY). D(x)=ix-E(x)f(x)dr. 4.D(X)=0的充要条件是X以概率1取常数C,即 其中)为概率密度 P[X=C)=1. ⊙⊙@ ④⊙@ 22019/11/19 2 数学期望的性质 1. 设C是常数, 则有E C  C.)( 2. 设X是一个随机变量, C是常数, 则有 E  CECX X).()( 3. 设X, Y 是两个随机变量, 则有 E X Y  E X  E Y ).()()( 4. 设X, Y 是相互独立的随机变量, 则有 E XY  E X E Y ).()()( 二维随机变量的数学期望              ,dd),( , )( yxyxxf px XE i j iji 同理可得 存在 则其期望值定义为 设 为二维随机变量 若 都 , YX ),( E X E Y )( ,)( , ),( ; X Y 的概率分布为 pij X Y ),( 的密度为f x y .),(              ,dd),( , )( yxyxyf py YE i j iji ),( ; X Y 的概率分布为 pij X Y ),( 的密度为f x y .),( 若 YX , .1 为离散型随机变量 yxg ),( , 是二元函数 ,   ,),()],([ i ij j YXgE ji pyxg ),( . 当 X Y 的联合概率分布为 pij YXgE )],([ yxyxfyxg ,dd),(),(       则 则 若 YX , .2 为连续型随机变量 yxg ),( , 是二元函数 , 当 YX ),( 的联合分布密度为 yxf .),( 方差的定义 )( .)( , ,})]({[)(Var)( ),(Var )( , })]({[ , })]({[ , 2 2 2 XD X XD XEXEX XD X XXEXE X XEXE 称 为标准差或均方差 记为 即 或 则称 是 的方差 记作 设 是一个随机变量 若 存在    方差的计算 ([)()( )] . 2 2  XEXEXD 离散型随机变量的方差 ([)( )] , 1 2 k k k  pXExXD    连续型随机变量的方差 ([)( )] ,d)( 2  xxfXExXD    其中 P kpxX 是 X 的分布律 . ,2,1 ,}{ k k   其中 xf )( 为概率密度. 方差的性质 1. 设 C 是常数, 则有 D C  .0)( 2. 设 X 是一个随机变量, C 是常数, 则有 ).()( 2  XDCCXD D X  Y  D X  D Y ).()()( 3. , , ( ), ( ) , 设 存在 X Y D X DY 相互独立 则 XD  0)(.4 的充要条件是 X 以概率 1 取常数 C ,即 P X  C  .1}{ 任课教师：王磊 概率论讲义Chapt4