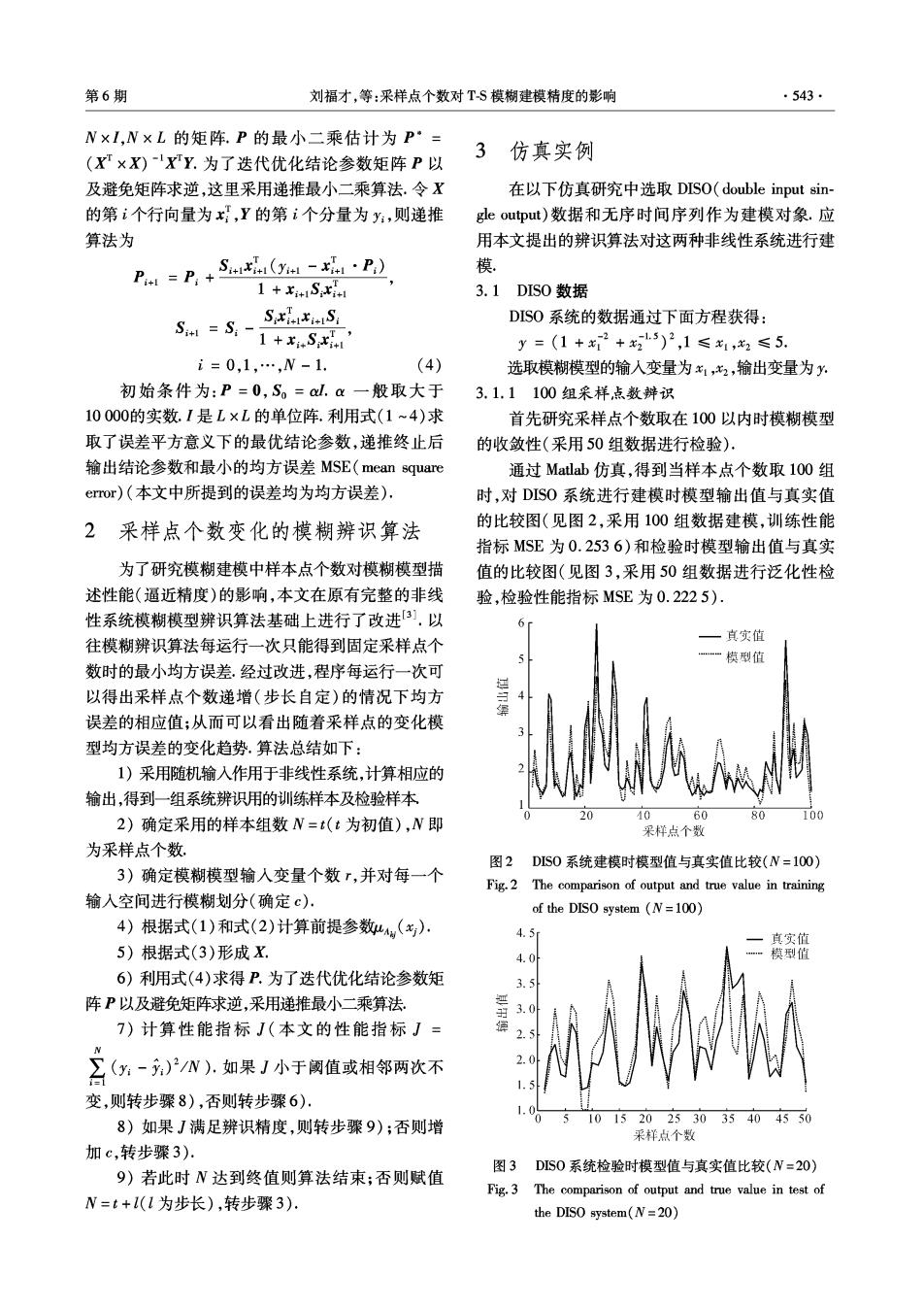
第6期 刘福才，等：采样点个数对TS模糊建模精度的影响 ·543· N×I,N×L的矩阵.P的最小二乘估计为P·= (X×X)xY.为了迭代优化结论参数矩阵P以 3仿真实例 及避免矩阵求逆，这里采用递推最小二乘算法.令X 在以下仿真研究中选取DISO(double input sin- 的第个行向量为x,Y的第i个分量为y,则递推 le output)数据和无序时间序列作为建模对象.应 算法为 用本文提出的辨识算法对这两种非线性系统进行建 P=P+S4e(u-4·P) 模。 1+Si 3.1DIS0数据 SXixiS DISO系统的数据通过下面方程获得： Sm=S-1+S y=(1+x2+x25)2,1≤x1,2≤5. i=0,1,…,W-1. (4) 选取模糊模型的输人变量为x1,x2,输出变量为y, 初始条件为：P=0,So=al,a一般取大于 3.1.1100组采样，点数辩识 10000的实数.I是L×L的单位阵.利用式(1~4)求 首先研究采样点个数取在100以内时模糊模型 取了误差平方意义下的最优结论参数，递推终止后 的收敛性（采用50组数据进行检验）. 输出结论参数和最小的均方误差MSE(mean square 通过Matlab仿真，得到当样本点个数取100组 eor)(本文中所提到的误差均为均方误差). 时，对DISO系统进行建模时模型输出值与真实值 2采样点个数变化的模糊辨识算法 的比较图（见图2，采用100组数据建模，训练性能 指标MSE为0.2536)和检验时模型输出值与真实 为了研究模糊建模中样本点个数对模糊模型描 值的比较图（见图3，采用50组数据进行泛化性检 述性能（逼近精度）的影响，本文在原有完整的非线 验，检验性能指标MSE为0.2225). 性系统模糊模型辨识算法基础上进行了改进3).以 —其实值 往模糊辨识算法每运行一次只能得到固定采样点个 一模型值 数时的最小均方误差.经过改进，程序每运行一次可 以得出采样点个数递增（步长自定）的情况下均方 误差的相应值：从而可以看出随着采样点的变化模 型均方误差的变化趋势.算法总结如下： 1)采用随机输入作用于非线性系统，计算相应的 输出，得到一组系统辨识用的训练样本及检验样本 10 60 80 100 2)确定采用的样本组数N=t(t为初值)，N即 采样点个数 为采样点个数. 图2DIS0系统建模时模型值与真实值比较(N=100) 3)确定模糊模型输人变量个数「，并对每一个 Fig.2 The comparison of output and true value in training 输入空间进行模糊划分（确定c). of the DISO system (N=100) 4)根据式(1)和式(2)计算前提参数4，(). 4.5 ,真实值 5)根据式(3)形成X. 4.0 模型值 6)利用式(4)求得P.为了迭代优化结论参数矩 3.5 阵P以及避免矩阵求逆，采用递推最小二乘算法， 3.0 7)计算性能指标J(本文的性能指标J= 2.5 名(-)N).如果J小于阈值或相邻两次不 2.0 1.5 变，则转步骤8)，否则转步骤6). 1. 8)如果J满足辨识精度，则转步骤9)；否则增 05101520253035404550 采样点个数 加c,转步骤3). 图3 DIS0系统检验时模型值与真实值比较(N=20) 9)若此时N达到终值则算法结束；否则赋值 Fig.3 The comparison of output and true value in test of N=t+1(1为步长)，转步骤3). the DISO system(N=20)