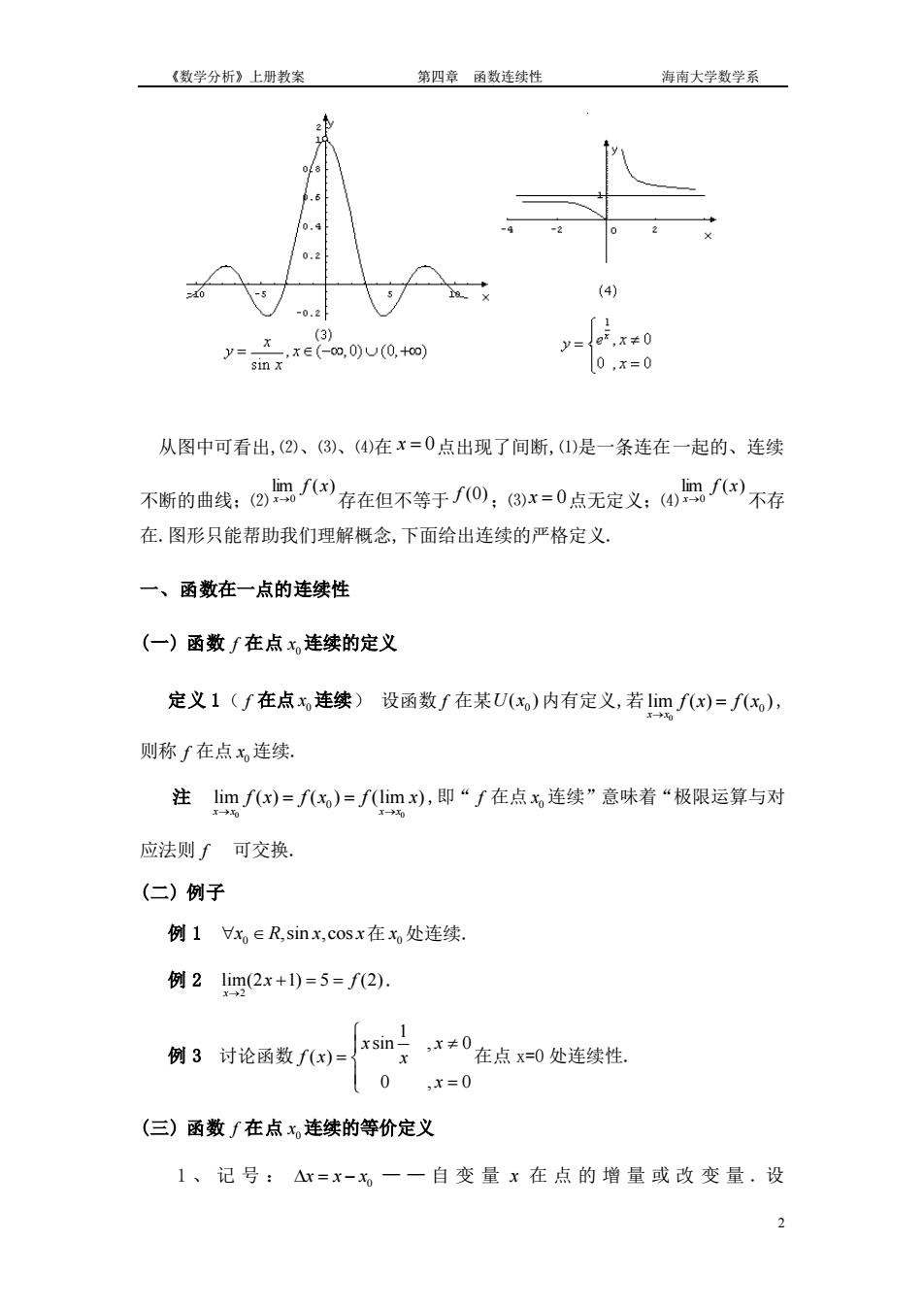
《数学分析》上册教案 第四章函数连续性 海南大学数学系 .6 0.2 (4) 0.2 e.(0.) 从图中可看出，(2)、（③）、(4在x=0点出现了间断，()是一条连在一起的、连续 不断的曲线：②职/)存在但不等于了0)，8x=0点无定义：④职不存 在.图形只能帮助我们理解概念，下面给出连续的严格定义. 一、函数在一点的连续性 (一)函数「在点x,连续的定义 定义1（∫在点x连续）设函数f在某U(x)内有定义，若1imfx)=fx), 则称∫在点x连续。 注imf)=f)=fimx),即“∫在点，连续”意味着“极限运算与对 应法则∫可交换， (二)例子 例1x∈R,sinx,cosx在x处连续. 例21im(2x+l)=5=f2). 例3讨论函数f(x)= xsin 天x≠0在点x=0处连续性 0x=0 (三)函数f在点x,连续的等价定义 1、记号：△x=x-x一一自变量x在点的增量或改变量.设《数学分析》上册教案 第四章 函数连续性 海南大学数学系 2 从图中可看出,⑵、⑶、⑷在 x = 0 点出现了间断,⑴是一条连在一起的、连续 不断的曲线；⑵ lim ( ) 0 f x x→ 存在但不等于 f (0) ；⑶ x = 0 点无定义；⑷ lim ( ) 0 f x x→ 不存 在.图形只能帮助我们理解概念,下面给出连续的严格定义. 一、函数在一点的连续性 (一) 函数 f 在点 0 x 连续的定义 定义 1（ f 在点 0 x 连续） 设函数 f 在某 0 U x( ) 内有定义,若 0 0 lim ( ) ( ) x x f x f x → = , 则称 f 在点 0 x 连续. 注 0 0 0 lim ( ) ( ) (lim ) x x x x f x f x f x → → = = ,即“ f 在点 0 x 连续”意味着“极限运算与对 应法则 f 可交换. (二) 例子 例 1 0   x R x x ,sin ,cos 在 0 x 处连续. 例 2 2 lim(2 1) 5 (2) x x f → + = = . 例 3 讨论函数 1 sin , 0 ( ) 0 , 0 x x f x x x    =    = 在点 x=0 处连续性. (三) 函数 f 在点 0 x 连续的等价定义 1 、记号 ： 0  = − x x x — — 自 变 量 x 在 点 的 增 量 或 改 变 量 . 设