
《数学分析》上册教案 第四章函数连续性 海南大学数学系 第四章函数的连续性 引言 在数学分析中,要研究种种不同性质的函数,其中有一类重要的函数,就是连 续函数.从今天开始,我们就来看看这类函数的特点.主要讲以下几个问题: 1,什么是“函数的连续性” 2.“间断”或“不连续”有哪些情形? 3.连续函数有哪些性质? 4.初等函数的连续性有何特点? §1连续性概念 教学目标:使学生深刻掌握函数连续性的概念和连续函数的概念 教学要求: 1、使学生深刻理解函数在一点连续包括单侧连续的定义,并能熟练写出函 数在一点连续的各种等价叙述: 2、应使学生从分析导致函数在一点不连续的所有可能的因素出发,理解函 数在一点间断以及函数间断点的概念,从反面加深对函数在一点连续这一 概念的理解力并能熟练准确地识别不同类型的间断点: 3、明确函数在一区间上连续是以函数在一点连续的概念为基础的,使学生 清楚区分“连续函数”与“函数连续”所表述的不同内涵。 教学重点:函数连续性概念 教学难点:函数连续性概念 教学过程: 引言 “连续”与“间断”(不连续)照字面上来讲,是不难理解的.如图: ,x≠0 2,x=0
《数学分析》上册教案 第四章 函数连续性 海南大学数学系 1 第四章 函数的连续性 引言 在数学分析中,要研究种种不同性质的函数,其中有一类重要的函数,就是连 续函数.从今天开始,我们就来看看这类函数的特点.主要讲以下几个问题: 1. 什么是“函数的连续性” 2. “间断”或“不连续”有哪些情形? 3. 连续函数有哪些性质? 4. 初等函数的连续性有何特点? §1 连续性概念 教学目标:使学生深刻掌握函数连续性的概念和连续函数的概念. 教学要求: 1、使学生深刻理解函数在一点连续包括单侧连续的定义,并能熟练写出函 数在一点连续的各种等价叙述; 2、应使学生从分析导致函数在一点不连续的所有可能的因素出发,理解函 数在一点间断以及函数间断点的概念,从反面加深对函数在一点连续这一 概念的理解力并能熟练准确地识别不同类型的间断点; 3、明确函数在一区间上连续是以函数在一点连续的概念为基础的,使学生 清楚区分“连续函数”与“函数连续”所表述的不同内涵. 教学重点:函数连续性概念. 教学难点:函数连续性概念. 教学过程: 引言 “连续”与“间断”(不连续)照字面上来讲,是不难理解的.如图:
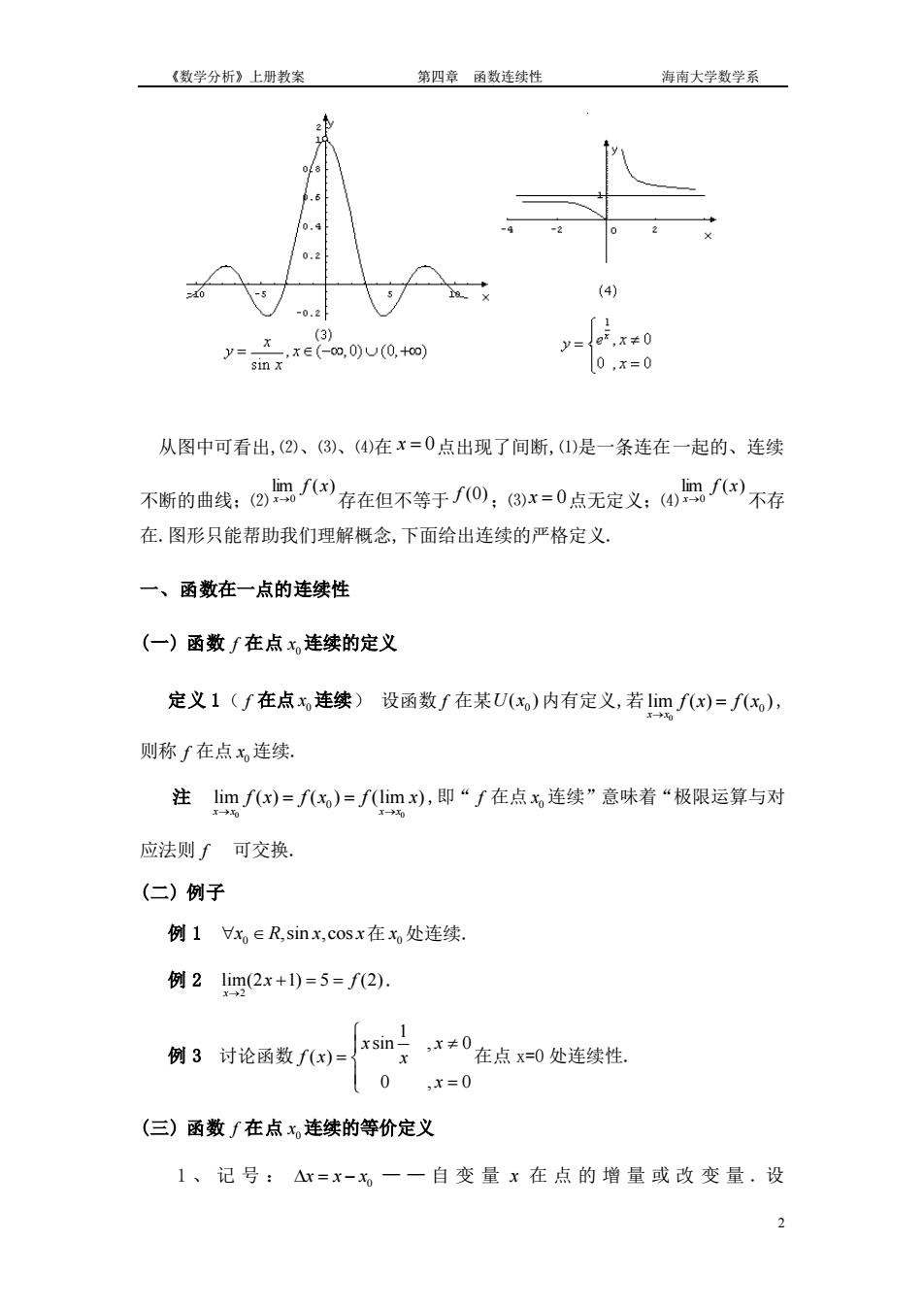
《数学分析》上册教案 第四章函数连续性 海南大学数学系 .6 0.2 (4) 0.2 e.(0.) 从图中可看出,(2)、(③)、(4在x=0点出现了间断,()是一条连在一起的、连续 不断的曲线:②职/)存在但不等于了0),8x=0点无定义:④职不存 在.图形只能帮助我们理解概念,下面给出连续的严格定义. 一、函数在一点的连续性 (一)函数「在点x,连续的定义 定义1(∫在点x连续)设函数f在某U(x)内有定义,若1imfx)=fx), 则称∫在点x连续。 注imf)=f)=fimx),即“∫在点,连续”意味着“极限运算与对 应法则∫可交换, (二)例子 例1x∈R,sinx,cosx在x处连续. 例21im(2x+l)=5=f2). 例3讨论函数f(x)= xsin 天x≠0在点x=0处连续性 0x=0 (三)函数f在点x,连续的等价定义 1、记号:△x=x-x一一自变量x在点的增量或改变量.设
《数学分析》上册教案 第四章 函数连续性 海南大学数学系 2 从图中可看出,⑵、⑶、⑷在 x = 0 点出现了间断,⑴是一条连在一起的、连续 不断的曲线;⑵ lim ( ) 0 f x x→ 存在但不等于 f (0) ;⑶ x = 0 点无定义;⑷ lim ( ) 0 f x x→ 不存 在.图形只能帮助我们理解概念,下面给出连续的严格定义. 一、函数在一点的连续性 (一) 函数 f 在点 0 x 连续的定义 定义 1( f 在点 0 x 连续) 设函数 f 在某 0 U x( ) 内有定义,若 0 0 lim ( ) ( ) x x f x f x → = , 则称 f 在点 0 x 连续. 注 0 0 0 lim ( ) ( ) (lim ) x x x x f x f x f x → → = = ,即“ f 在点 0 x 连续”意味着“极限运算与对 应法则 f 可交换. (二) 例子 例 1 0 x R x x ,sin ,cos 在 0 x 处连续. 例 2 2 lim(2 1) 5 (2) x x f → + = = . 例 3 讨论函数 1 sin , 0 ( ) 0 , 0 x x f x x x = = 在点 x=0 处连续性. (三) 函数 f 在点 0 x 连续的等价定义 1 、记号 : 0 = − x x x — — 自 变 量 x 在 点 的 增 量 或 改 变 量 . 设

《数学分析》上册教案 第四章函数连续性 海南大学数学系 %=f),4y=f(x)-fx)=f(x+△)-fx)=y-片一一函数y在点x的增 量 注自变量的增量△x或函数的增量△y可正、可负、也可为零.(区别于“增 加”) 2、价定义1:函数f在点x连续一1m4y=0. 3、价定义2:函数f在点。连续一e>0,6>0,当Ix-xk6 时,lfx)-f(x)k6. 注一个定义是等价的,根据具体的问题选用不同的表述方式如用三种定义, 可以证明以下命题: 例4证明函数fx)=xDx)在点x=0连续,其中D(x)为Dirichlet函数. (四)函数f在点x有极限与函数∫在点x,连续之间的关系 1、对邻域的要求看:在讨论极限时,假定∫在U(x)内不定义(∫在点x可 以没有定义).而∫在点x,连续则要求∫在某U(x,)内有定义(包括x). 2、极限中,要求0x-xk6,而当“∫在点x连续”时,由于x=x 时,lf(x)-f(x)水k恒成立.所以换为:|x-xk6. 3、从对极限的要求看:“∫在点x连续”不仅要求“∫在点x有极限”,而 且mfx)=f6:而在讨论mf)时,不要求它等于f化),甚至于 f(x)可以不存在. 总的来讲,函数在点x,连续的要求是:①f(x)在点x有定义:②imfx)存 在:回1mf八)=f).任何一条不满足,∫在点6就不连续.同时,由定义可知, 函数在某点是可连续,是函数在这点的局部性质, (五)∫在点,左(右)连续定义 1、定义 3
《数学分析》上册教案 第四章 函数连续性 海南大学数学系 3 0 0 y f x = ( ), 0 0 0 0 = − = + − = − y f x f x f x x f x y y ( ) ( ) ( ) ( ) ——函数 y 在点 0 x 的增 量. 注 自变量的增量 x 或函数的增量 y 可正、可负、也可为零.(区别于“增 加”). 2、价定义 1:函数 f 在点 0 x 连续 0 lim 0 x y → = . 3、价定义 2 :函数 f 在 点 0 x 连 续 0, 0 , 当 0 | | x x − 时, 0 | ( ) ( ) | f x f x − . 注 一个定义是等价的,根据具体的问题选用不同的表述方式.如用三种定义, 可以证明以下命题: 例 4 证明函数 f x xD x ( ) ( ) = 在点 x = 0 连续,其中 D x( ) 为 Dirichlet 函数. (四) 函数 f 在点 0 x 有极限与函数 f 在点 0 x 连续之间的关系 1、对邻域的要求看:在讨论极限时,假定 f 在 0 0 U x( ) 内不定义( f 在点 0 x 可 以没有定义).而 f 在点 0 x 连续则要求 f 在某 0 U x( ) 内有定义(包括 0 x ). 2、极限中,要求 0 0 | | − x x ,而当“ f 在点 0 x 连续”时,由 于 x= 0 x 时, 0 | ( ) ( ) | f x f x − 恒成立.所以换为: 0 | | x x − . 3、从对极限的要求看:“ f 在点 0 x 连续”不仅要求“ f 在点 0 x 有极限”,而 且 0 0 lim ( ) ( ) x x f x f x → = ;而在讨论 0 lim ( ) x x f x → 时,不要求它等于 0 f x( ) ,甚至于 0 f x( ) 可以不存在. 总的来讲,函数在点 0 x 连续的要求是:① f x( ) 在点 0 x 有定义;② 0 lim ( ) x x f x → 存 在;③ 0 0 lim ( ) ( ) x x f x f x → = . 任何一条不满足, f 在点 0 x 就不连续.同时,由定义可知, 函数在某点是可连续,是函数在这点的局部性质. (五) f 在点 0 x 左(右)连续定义 1、定义

《数学分析》上册教案 第四章函数连续性 海南大学数学系 定义2:设函数f在点U.()(U.(x)内有定义),若m)=f,) (imfx)=fx),则称f在点,右(左)连续. 2、∫在点x,连续的等价刻划 定理4.1函数∫在点,连续一∫在点x既是右连续,又是左连续. 如上例4:mxD()=1mx=0=f0)(右连续),ImxD()=lmx=0=f0) (左连续), {一-之0在点x=0的连续性 例5讨论函数f=+2¥≥0 例6设 [sinx r0 其中a、b为常数.问:①。、b为何值时,/存在?②。、b为何值 时,f)在x=0点连续? 解即),画f)=6,故0b=1,a为任意常数时,f刊存在: (2)欲使f(x)在x=0点连续,应有a=1=b 二、区间上的连续函数 (一)定义 若函数∫在区间1上每一点都连续,则称∫为I上的连续函数.对于闭区间 或半开半闭区间的端点,函数在这些点上连续是指左连续或右连续,若函数∫在 区间[a,]上仅有有限个第一类间断点,则称∫在[a,b]上分段连续. (二)例子
《数学分析》上册教案 第四章 函数连续性 海南大学数学系 4 定义 2:设函数 f 在点 0 U x( ) + ( 0 U x( ) − 内有定义),若 0 0 lim ( ) ( ) x x f x f x → + = ( 0 0 lim ( ) ( ) x x f x f x → − = ),则称 f 在点 0 x 右(左)连续. 2、 f 在点 0 x 连续的等价刻划 定理 4.1 函数 f 在点 0 x 连续 f 在点 0 x 既是右连续,又是左连续. 如上例 4: 0 0 lim ( ) lim 0 (0) x x xD x x f → → + + = = = (右连续), 0 0 lim ( ) lim 0 (0) x x xD x x f → → − − = = = (左连续). 例 5 讨论函数 2, 0 ( ) 2, 0 x x f x x x + = − 在点 x = 0 的连续性. 例 6 设 sin , 0 ( ) , 0 1 sin , 0 x x x f x a x x b x x = = + , 其中 a、b 为常数.问:⑴ a 、b 为何值时, lim ( ) 0 f x x→ 存在? ⑵ a 、b 为何值 时, f (x) 在 x = 0 点连续? 解 lim ( ) 1 0 = → − f x x , f x b x = → + lim ( ) 0 ,故⑴ b =1, a 为任意常数时, lim ( ) 0 f x x→ 存在; ⑵ 欲使 f (x) 在 x = 0 点连续,应有 a =1= b 二、区间上的连续函数 (一) 定义 若函数 f 在区间I上每一点都连续,则称 f 为I上的连续函数.对于闭区间 或半开半闭区间的端点,函数在这些点上连续是指左连续或右连续.若函数 f 在 区间 [ , ] a b 上仅有有限个第一类间断点,则称 f 在 [ , ] a b 上分段连续. (二) 例子

《数学分析》上册教案 第四章函数连续性 海南大学数学系 1、函数y=C,y=x,y=sinx,y=cosx是R上的连续函数: 2、函数y=√-x2在(-1,1)内每一点都连续.在x=1处为左连续,在x=-1处 为右连续,因而它在[-1,】上连续. 命题初等函数在其定义区间上为连续函数 函数y=[x,y=sgnx在-l,】上是分段连续的y=[闲在R上是分段连续吗? sgnx在R上是分段连续吗? 三、间断点及其分类 (一)不连续点(间断点)定义 定义3设函数f在某U(x)内有定义,若∫在点x无定义,或∫在点x有 定义而不2,不则称点x,为函数∫的间断点或不连续点. 注这个定义不好:还不如说:设∫在U(x)内不定义,如果f(x)在x,不连 续,则称x是x)的不连续点(或间断点).由上述分析可见,若为函数∫的间 断点,则必出现下列情形之一:①fx)在点x无定义:②mf)不存在:③ mfx)≠f,).据此,对函数的间断点作如下分类: (二)间断点分类 1、去间断点若limf(x)=A,而f在点x,无定义,或有定义但f,)≠A,则 称x,为∫的可去间断点。 例如:x=0是函数HsgnxL8()=s血的可去间断点 “可去间断点”名称何来?通过一定的手段,可以“去掉”.设x。是f(x)的可 去间断点,且只=A7树则飞是7元的莲续点 Ax≠x0 例如,对g)=nx,定义g={ x0,则到在x=0连续 (1x=0 5
《数学分析》上册教案 第四章 函数连续性 海南大学数学系 5 1、函数 y C y x y x y x = = = = , , sin , cos 是R上的连续函数; 2、函数 2 y x = −1 在 ( 1,1) − 内每一点都连续.在 x =1 处为左连续,在 x =−1 处 为右连续,因而它在 [ 1,1] − 上连续. 命题 初等函数在其定义区间上为连续函数. 函数 y x = [ ] , y x = sgn 在 [ 1,1] − 上是分段连续的 y x = [ ] 在R上是分段连续吗? sgn x 在R上是分段连续吗? 三、间断点及其分类 (一) 不连续点(间断点)定义 定义 3 设函数 f 在某 0 0 U x( ) 内有定义,若 f 在点 0 x 无定义,或 f 在点 0 x 有 定义而不 2,不则称点 0 x 为函数 f 的间断点或不连续点. 注 这个定义不好;还不如说:设 f 在 0 0 U x( ) 内不定义,如果 f x( ) 在 0 x 不连 续,则称 0 x 是 f x( ) 的不连续点(或间断点).由上述分析可见,若 0 x 为函数 f 的间 断点,则必出现下列情形之一:① f x( ) 在点 0 x 无定义;② 0 lim ( ) x x f x → 不存在;③ 0 0 lim ( ) ( ) x x f x f x → .据此,对函数的间断点作如下分类: (二) 间断点分类 1、去间断点 若 0 lim ( ) x x f x A → = ,而 f 在点 0 x 无定义,或有定义但 0 f x A ( ) ,则 称 0 x 为 f 的可去间断点. 例如: x = 0 是函数 sin ( ) | sgn |, ( ) x f x x g x x = = 的可去间断点. “可去间断点”名称何来?通过一定的手段,可以“去掉”.设 0 x 是 f x( ) 的可 去间断点,且 0 lim ( ) x x f x A → = . 0 0 ( ), ( ) , f x x x f x A x x = 则 0 x 是 f x( ) 的连续点. 例如,对 sin ( ) x g x x = ,定义 sin , 0 ( ) 1, 0 x x g x x x = = ,则 g x( ) 在 x = 0 连续

《数学分析》上册教案 第四章函数连续性 海南大学数学系 2、跃间断点若1mfx,im)存在,但f优+0以f伍-0,则称点x为 函数∫的跳跃间断点. 例如,对y=x,lim[闲=0,lim[x)=-1故x=0是它的跳跃间断点。 再如x=0是sgnx的跳跃间断点。 可去间断点与跳跃间断点统称为第一类间断点,其特点的函数在该点处的左、 右极限都存在 3、二类间断点函数的所有其它形式的间断点(即使称函数至少有一侧极 限不存在的点)称为函数的第二类间断点. 例如,x=0是函数:,sn上的第二类间断点。 定理f田)在(a)上单调,若点无为函数∫的间断点,则点飞必是∫的第 一类间断点. 证明无妨设f在(a,b)单调上升,x∈a,),当r→。-0时,函数值 )单调上升,有上界),所以极限存在,且f国=f代化-0)≤f) 同理0田=f化+0)2f化,) 若f,-0)=f+0),为f)连续点,若f-0)<f+0),为第 一类间断点。 例7讨论函数-1x-的间断点类型 x(x2-D) 例8延拓函数)-如3江,使在点,=0连续, 的举出定义在0】上且仅在点:一子号三点间断的函数的子。 例l0讨论Dirichlet函数D(x)和Riemann函数R(x)的连续性. 作业教材P73-741(1),2(6)(7),3-6:
《数学分析》上册教案 第四章 函数连续性 海南大学数学系 6 2、跃间断点 若 0 0 lim ( ), lim ( ) x x x x f x f x → → + − 存在,但 0 0 f x f x ( 0), ( 0) + − ,则称点 0 x 为 函数 f 的跳跃间断点. 例如,对 y x = [ ] , 0 0 lim[ ] 0, lim[ ] 1 x x x x → → + − = = − 故 x = 0 是它的跳跃间断点. 再如 x = 0 是 sgn x 的跳跃间断点. 可去间断点与跳跃间断点统称为第一类间断点,其特点的函数在该点处的左、 右极限都存在. 3、二类间断点 函数的所有其它形式的间断点(即使称函数至少有一侧极 限不存在的点)称为函数的第二类间断点. 例如, x = 0 是函数 1 x , 1 sin x 的第二类间断点. 定理 f (x) 在 (a,b) 上单调,若点 0 x 为函数 f 的间断点,则点 0 x 必是 f 的第 一类间断点. 证明 无妨设 f (x) 在 (a,b) 单调上升, ( , ) x0 a b ,当 x → x0 − 0 时,函数值 f (x) 单调上升,有上界 ( ) 0 f x ,所以极限存在,且 lim ( ) ( 0) ( ) 0 0 0 0 f x f x f x x x = − → − . 同理 lim ( ) ( 0) ( ) 0 0 0 0 f x f x f x x x = + → + . 若 ( 0) ( 0) f x0 − = f x0 + , 0 x 为 f (x) 连续点,若 ( 0) ( 0) f x0 − f x0 + , 0 x 为第 一类间断点. 例7 讨论函数 ( 1) ( 1) ( ) 2 − − = x x x x f x 的间断点类型. 例8 延拓函数 , sin 3 ( ) x x f x = 使在点 x0 = 0 连续. 例9 举出定义在[0,1]上且仅在点 4 1 , 3 1 , 2 1 x = 三点间断的函数的例子. 例10 讨论 Dirichlet 函数 D(x) 和 Riemann 函数 R(x) 的连续性. 作业 教材 P73—74 1 (1),2 (6)(7), 3—6;