
《数学分析》上册教案 第五章导数与微分 海南大学数学系 §2求导法则 教学章节:第五章导数与微分一一§2求导法则 教学目标:熟悉导数的运算性质和求导法则,牢记基本初等函数的导数公式,并熟练进行初等函 数的导数运算 教学要求:熟练掌握导数的四则运算法则,复合函数的求导法则:会求反函数的导数,并在熟记基 本初等函数导数公式的基础上综合运用这些法则与方法熟练准确地求出初等函数 的导数。 教学重点:导数的四则运算法则、复合函数求导法则、反函数求导法: 散学难点:复合函数求导法则及复合函数导数的计算. 教学方法:以问题教学法为主,结合课堂练习. 教学过程: 引言 上一节我们讲述了导数的相关知识,要求大家:深刻理解导数概念,能准确表达其定义:明确 其物理、几何意义,会求曲线上一点的切线方程:能够从定义出发求某些函数的导数:知道导数与 导函数的区别和联系:明确导数与单侧导数,可导与连续的关系特别要注意,要学会从导数定义 出发求某些导数的导数.例如,我们上节课已计算出左边所列的导函数,并且我们知道,计算函数 在一点的导数或某区间上的导函数归结为极限的计算.因此,从理论上来讲,给了一个函数(不管 它是简单函数,还是复杂函数),总可用定义求其导数(只要极限存在).但从我们计算左边几个 函数的经验知道,用定义计算函数的导数是比较繁琐的.试想对基本初等函数的导数计算(用定 义求导)都如此繁琐,对一般的初等函数更是不可想象 因此,我们不能满足于只用导数定义求导数,而应去寻找一些求导数的一般方法,以便能较 方便地求出初等函数的导数.在给出较一般的方法之前,先看以下函数如何求导数: (x)=sin x+cosx gi(x)=sin 2x f(x)=sin x.cosx g2(x)=sin(ax) coSx g(x)=arcsinx f(x)=csinx ga(x)=arccosx 一、导数的四则运算
《数学分析》上册教案 第五章 导数与微分 海南大学数学系 1 §2 求导法则 教学章节:第五章 导数与微分——§2 求导法则 教学目标:熟悉导数的运算性质和求导法则,牢记基本初等函数的导数公式,并熟练进行初等函 数的导数运算. 教学要求:熟练掌握导数的四则运算法则,复合函数的求导法则;会求反函数的导数,并在熟记基 本初等函数导数公式的基础上综合运用这些法则与方法熟练准确地求出初等函数 的导数. 教学重点:导数的四则运算法则、复合函数求导法则、反函数求导法; 教学难点:复合函数求导法则及复合函数导数的计算. 教学方法:以问题教学法为主,结合课堂练习. 教学过程: 引言 上一节我们讲述了导数的相关知识,要求大家:深刻理解导数概念,能准确表达其定义;明确 其物理、几何意义,会求曲线上一点的切线方程;能够从定义出发求某些函数的导数;知道导数与 导函数的区别和联系;明确导数与单侧导数,可导与连续的关系.特别要注意,要学会从导数定义 出发求某些导数的导数.例如,我们上节课已计算出左边所列的导函数,并且我们知道,计算函数 在一点的导数或某区间上的导函数归结为极限的计算.因此,从理论上来讲,给了一个函数(不管 它是简单函数,还是复杂函数),总可用定义求其导数(只要极限存在).但从我们计算左边几个 函数的经验知道,用定义计算函数的导数是比较繁琐的.试想对基本初等函数的导数计算(用定 义求导)都如此繁琐,对一般的初等函数更是不可想象. 因此,我们不能满足于只用导数定义求导数,而应去寻找一些求导数的一般方法,以便能较 方便地求出初等函数的导数.在给出较一般的方法之前,先看以下函数如何求导数: f (x) sin x cos x 1 = + g (x) sin 2x 1 = f (x) sin x cos x 2 = ( ) sin( ) g2 x = ax x x f x a log cos ( ) 3 = g (x) arcsin x 3 = f (x) csin x 4 = g (x) arccos x 4 = 一、导数的四则运算

《数学分析》上册教案 第五章导数与微分 海南大学数学系 问题1设f(x)=sinx±cosx,求(x): 分析利用导数的定义及极限的四则运算知,厂(x)=cosx干sinx=(snx)士(cosx).即 (sin x+cosx)=(sin x)'(cosx)' 一般地,有如下和的导法则: 定理1(和的导数)设f(x),()在x点可导,则 [f(x)±g(x)=f(x)±g(x)(求导是线性运算) 证明令x)=f(x)+gx) y-[fx+△x)+gx+△x】-[fx)+gx] Ar -f(x+Ax)-f(x).g(x+Ax)-g(x) →f"(x)+g'(x)当△r→0时。 问题2设f(x)=snxa,则(x)=(sinx)-(a'Y=cosx·a.ha对吗? 分析一般地,有如下乘积的求导法则: 定理2(积的导数)设f(x),x)在x点可导,则 [fx)g(x)川=f"(x)g(x)+fx)g(x)(它导它不导,它不导它导,然后加起来) 证明 令x)-fx)g(x) 是-九+8-/8四 △r (分子-f(x)gx+△r)+f(x)gx+△x》 :但a+a+ △r →f"(x)g(x)+f(x)g'(x)当△x→0时。 1 (u(x)v(x)w(x)y(xo)=u(xo)v(xo)w(xo)+u(xo)v(xo)w(xo)+uo)v(xo)w'(xo) 推论2若函数(x)在x知可导,C为常数,则(Co(x),=Cv(x) 月题3设国=求r 分析:. 一般地,存如下商的运算法则: 定理3(商的导数)设/),8)在x点可导,则
《数学分析》上册教案 第五章 导数与微分 海南大学数学系 2 问题 1 设 f (x) = sin x cos x ,求 f '(x) . 分析 利用导数的定义及极限的四则运算知, f '(x) = cos x sin x = (sin x)'(cos x)' .即 (sin x cos x)'= (sin x)'(cos x)' 一般地,有如下和的导法则: 定理 1(和的导数) 设 f (x) , g(x) 在 x 点可导,则 [ f (x) g(x)] = f (x) g(x) (求导是线性运算) 证明 令 y(x) = f (x) + g(x) ( ) ( ) 当 0时。 ( ) ( ) ( ) ( ) [ ( ) ( )] [ ( ) ( )] → + → + − + + − = + + + − + = f x g x x x g x x g x x f x x f x x f x x g x x f x g x x y 问题 2 设 x f (x) = sin x a ,则 f x x a x a a x x '( ) = (sin )'( )'= cos ln 对吗? 分析 一般地,有如下乘积的求导法则: 定理 2(积的导数)设 f (x) , g(x) 在 x 点可导,则 [ f (x) g(x)] = f (x) g(x) + f (x) g(x) (它导它不导,它不导它导,然后加起来) 证明 令 y(x) = f (x) g(x) 当 时。 分子 ( ) ( ) ( ) ( ) 0 ( ) ( ) ( ) ( ) ( ) ( ) ( ( ) ( ) ( ) ( )) ( ) ( ) ( ) ( ) → + → + − + + + − = − + + + + + − = f x g x f x g x x x g x x g x g x x f x x f x x f x f x g x x f x g x x x f x x g x x f x g x x y 推论 1 ( ( ) ( ) ( ))'( ) '( ) ( ) ( ) ( ) '( ) ( ) ( ) ( ) '( ) 0 0 0 0 0 0 0 0 0 0 u x v x w x x = u x v x w x + u x v x w x + u x v x w x . 推论 2 若函数 v(x) 在 0 x 知可导,C 为常数,则 (cos( ))' '( ) 0 0 x C v x x x = = . 问题 3 设 x a f x a x log ( ) = ,求 f '(x) . 分析: . 一般地,存如下商的运算法则: 定理 3(商的导数) 设 f (x) , g(x) 在 x 点可导,则

《数学分析》上册教案 第五章导数与微分 海南大学数学系 [f田]-xgx)-fx8田 Lg(x)] g2(x) 证明令)= 1 (x) 4y1「1 11 △Axg(x+△x)gx)] =-86r+A)-g). 1 g(x+△x)g(x) →得 当Ar→0时 得动 1 给出(3) 推论(1)[【cfx)=cfx). (2) [空]-2 (3) 0网-2K国.K国=国-四 △.利用导数的四则运算法则举例. 例1fx)=x3+5x2-9x+元,求f(x),f(0). 例2y=cosxinx,求川a 例3证明:(xy=-m,neN* 例4证明:((tanx)'=sec2x,(cotxY-=csc2x. 例5证明:(sec xy=-sec xtan x,(cscxy=-cscxcotx 4.利用导数的四则运算法则求导数举例: 1.f(x)=x2+sinx: 2.f(x)=x2-sin x+cosx 3.fx)=2x2; 4.f(x)=x2cosx
《数学分析》上册教案 第五章 导数与微分 海南大学数学系 3 ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 g x f x g x f x g x g x f x − = . 证明 令 ( ) 1 ( ) g x y x = 当 0 时。 ( ) ( ) ( ) ( ) ( ) ( ) 1 ( ) 1 ( ) 1 1 2 → → − + + − = − − + = x g x g x x g x x g x g x x g x x x g x x g x y ( ) 1 ( ) ( ) ( ) g x f x g x f x = 给出(3). 推论 (1) [c f (x)] = c f (x) . (2) = = = n i i n i i f x f x 1 1 ( ) ( ) . (3) ( ) ( ) , ( ) ( ) ( ) ( ) 1 1 1 f x K x K x f x f x f x k k n n k k n j i = = = = . .利用导数的四则运算法则举例. 例 1 f (x) = x + 5x − 9x + 3 2 ,求 f '(x) , f '(0) . 例 2 y = cos x ln x ,求 x= y' . 例 3 证明: 1 ( )' − − − = − n n x nx , + n N . 例 4 证明: x x 2 (tan )'= sec , x x 2 (cot )'= csc . 例 5 证明: (sec x)'= sec x tan x , (csc x)'= −csc x cot x . .利用导数的四则运算法则求导数举例: 1. f (x) x sin x 2 = + ; 2. f (x) x sin x cos x 3 = − + ; 3. 2 f (x) = 2x ; 4. f (x) x cos x 2 = ;

《数学分析》上册教案 第五章导数与微分 海南大学数学系 5.f(x)=xsin x+7x 6.f(x)=x+x2+x'cosx: 7.f)snxx 8.f)=5smx+3g。 x 0.yh. 二、反函数的导数 问题1设fx)=arcsinx,求f(x) 分析. 一般地,存如下结果: 定理4设x=p0)在区间(c,d)上连续,严格上升,在%∈(,d山点可导,且0)+0, x。=).则反函数y=f)在x0点可导,且 1 1 fx,)-pp】. 注若x=)在(c,)可导,导数>0(或0(或<0)可推出)严格上升(下降),反函数之导数公式也可写成 少= 定理的证到要证) ”X一。存在,注意到这个比式是函数 y-6 80=-o)与y=w 的复合,由定理条件知 =得得只w四”d 1 1 y-0
《数学分析》上册教案 第五章 导数与微分 海南大学数学系 4 5. f (x) = x sin x + 7x ; 6. f (x) x x x cos x 2 3 = + + ; 7. x tgx f (x) = x sin x ln x + 2 ; 8. x x tgx f x 5sin 3 ( ) + = ; 9. x x tgx e x y x ln 1 sin 2 + + = . 二、反函数的导数 问题 1 设 f (x) = arcsin x ,求 f '(x) . 分析 . 一般地,存如下结果: 定理 4 设 x = ( y) 在区间 (c, d ) 上连续,严格上升,在 ( , ) y0 c d 点可导,且 ( y0 ) 0 , ( ) 0 0 x = y .则反函数 y = f (x) 在 0 x 点可导,且 [ ( )] 1 ( ) 1 ( ) 0 0 0 y f x f x = = . 注 若 x = ( y) 在 (c, d ) 可导,导数 0 (或 0) ,则反函数 y = f (x) 存在,且 ( ) ( ) 1 [ ( )] 1 ( ) 1 ( ) y f x y y f x f x = = = = . 这里导数 0 (或 0) 可推出 ( y) 严格上升(下降),反函数之导数公式也可写成 dy dx dx dy 1 = . 定理的证明 要证 0 0 ( ) ( ) lim 0 x x f x f x x x − − → 存在,注意到这个比式是函数 ( ) ( ) ( ) 0 0 y y y y g y − − = 与 y = f (x) 的复合,由定理条件知 ( ) 1 0 ) 0 ( ) ( 1 lim ( ) ( ) ( ) ( ) lim 0 0 0 0 0 y y y y y y y f x f x y y y y = − − = − − → →
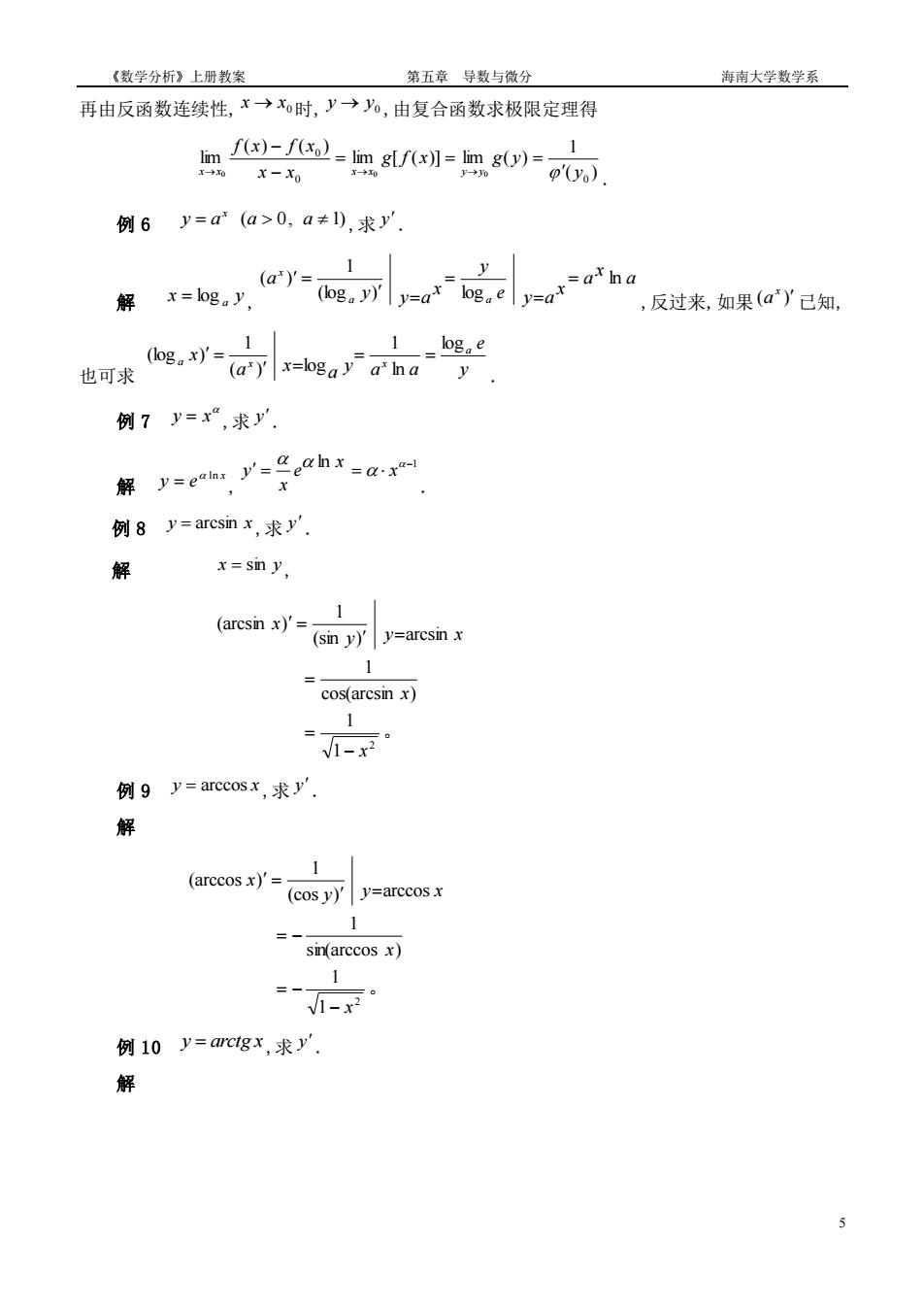
《数学分析》上册教案 第五章导数与微分 海南大学数学系 再由反函数连续性,术→时,y→%,由复合函数求极限定理得 只-Re=g- 1 x-Xo 例6y=a(a>0,a≠),求y 1 y 解x=g,y,“ ,反过来,如果(a)y已知, ere广h。 1 logae 也可求 例7y=“,求y 解=e广名eah=r 例8y=arcsin,求y. 解 x=sin y 1 (arcsn )(sin y yaresnx 1 例9y=arccosx,求y. 1 (arccos x)'=- (cosy)y=arccosx sin(arccos x) V1-x2 例10y=acgx,求y'. 解
《数学分析》上册教案 第五章 导数与微分 海南大学数学系 5 再由反函数连续性, 0 x → x 时, 0 y → y ,由复合函数求极限定理得 ( ) 1 lim [ ( )] lim ( ) ( ) ( ) lim 0 0 0 0 0 0 y g f x g y x x f x f x x x x x y y = = = − − → → → . 例 6 y = a (a 0, a 1) x ,求 y . 解 x y a = log , a x a x e y a y x y y a a a a x ln (log ) log 1 ( ) = = = = = ,反过来,如果 ( ) x a 已知, 也可求 y e a x a y a a x a a x x log ln 1 ( ) log 1 (log ) = = = = . 例 7 y = x ,求 y . 解 x y e ln = , ln −1 = = x x e x y . 例 8 y = arcsin x ,求 y . 解 x = sin y , 。2 1 1 cos(arcsin ) 1 (sin ) arcsin 1 (arcsin ) x x y y x x − = = = = 例 9 y = arccos x ,求 y . 解 。2 1 1 sin(arccos ) 1 arccos (cos ) 1 (arccos ) x x y y x x − = − = − = = 例 10 y = arctg x,求 y . 解

《数学分析》上册教案 第五章导数与微分 海南大学数学系 (arctgx)(yy-arctgx 1 1 se(arctgx) 同理可得((arxy=1+子 三、复合函数的导数 问题1设f(x)=sn2x,求(x):2).设fx)=sim(a),求厂(x):3).设fx)=x“,求 f(x). 定理5设∫4,)与8)存在,山=8,),则复合函数Fx)=八g(x在点可导,且 F'(x)=f"Lg(x月g'(x) 注若f)的定义域包含“=(x)的值域,两函数在各自的定义域上可导,则复合函数 F(x)=f几g(x川在g(x)的定义域上可导,且 F'(x)=fTg(x】g(x)(怀中抱月) 或 =必4, _少.du dx du dx 定理的证明定义函数 f0-f,u≠6 4(0)=u-6 f"(4),=4· 4在“,点连续,回4w=4%)=f) 由恒等式,f四-f4,)=4uu-),我们有 F)-F_Lg-1&,】-g川:8)-8 x-Xo x-Xo x-Xo 令x→,得F()=fg(x小g'(x) 我们引进4(四)是为了避免再直接写表达式
《数学分析》上册教案 第五章 导数与微分 海南大学数学系 6 2 。 2 1 1 sec ( ) 1 ( ) 1 ( ) x arctg x tg y y arctg x arctg x + = = = = 同理可得 2 1 1 ( ) x arcctg x + = − . 三、复合函数的导数 问题 1 设 f (x) = sin 2x ,求 f '(x) ;2). 设 ( ) sin( ) x f x = a ,求 f '(x) ;3). 设 f (x) = x ,求 f '(x) . 定理 5 设 ( ) u0 f 与 ( ) 0 g x 存在, ( ) 0 0 u = g x ,则复合函数 F(x) = f [g(x)] 在 0 x 点可导,且 ( ) [ ( )] ( ) 0 0 0 F x = f g x g x . 注 若 f (u) 的定义域包含 u = g(x) 的值域,两函数在各自的定义域上可导,则复合函数 F(x) = f [g(x)] 在 g(x) 的定义域上可导,且 F(x) = f [g(x)] g(x) (怀中抱月) 或 x u ux y = y , dx du du dy dx dy = . 定理的证明 定义函数 = − − = 0 0。 0 0 0 ( ) , , , ( ) ( ) ( ) f u u u u u u u f u f u A u A(u) 在 0 u 点连续, lim ( ) ( ) ( ) 0 0 0 A u A u f u u u = = → . 由恒等式, ( ) ( ) ( )( ) u0 A u u u0 f u − f = − ,我们有 0 0 0 0 0 0 ( ) ( ) [ ( )] ( ) ( ) [ ( )] [ ( )] x x g x g x A g x x x f g x f g x x x F x F x − − = − − = − − 令 0 x → x ,得 ( ) [ ( )] ( ) 0 0 0 F x = f g x g x . 我们引进 A(u) 是为了避免再直接写表达式

《数学分析》上册教案 第五章导数与微分 海南大学数学系 F(x)-F(x)_f(u)-f(uo).g(x)-g(xo) x-xo u-14o X-xo 中当x≠。时,可能会出现“=4情况 例1y=-,求y 解 y-j0-x)a-x) =0-x)(-2x -x1 例2y=snx之,求y y'=cosx2.(x2)'=2xcosx2 例3y=sin(sin),求y y'=cos(sin x).cosx.(x)'=3x2 cosx'cos(sin x) 例4y=x+1+),求y y=《++ry1 2x 21+x2 x+1+x2 +++ 例5y=血x,求y ,≠0时,hxy= 例6y=hsim(2x),求y y2o2-22到 2 解 sin(2x) 四、隐函数微分法 若可微函数)=)满足方程F)=0,则其导数可以从孟F川- 求出.一个方程 F(x)=0何时能唯一决定一个可微函数y=),留待日后解决,现在我们通常假定能唯一决 定一个可微函数,考虑如何求出导函数问题
《数学分析》上册教案 第五章 导数与微分 海南大学数学系 7 0 0 0 0 0 0 ( ) ( ) ( ) ( ) ( ) ( ) x x g x g x u u f u f u x x F x F x − − − − = − − 中当 0 x x 时,可能会出现 u = u0 情况. 例 1 2 y = 1− x ,求 y . 解 。2 2 1 2 2 1 2 1 2 1 (1 ) ( 2 ) 2 1 (1 ) (1 ) 2 1 x x x x y x x − = − = − − = − − − − 例 2 2 y = sin x ,求 y . 解 2 2 2 y = cos x (x ) = 2x cos x . 例 3 sin(sin ) 3 y = x ,求 y . 解 cos(sin ) cos ( ) 3 cos cos(sin ) 3 3 3 2 3 3 y = x x x = x x x . 例 4 ln( 1 ) 2 y = x + + x ,求 y . 解 2 2 2 2 2 1 1 1 2 1 2 1 1 ( 1 ) x x x x x x x x x y + = + + + + = + + + + = . 例 5 y = ln | x | ,求 y . 解 x 0 时, x y 1 = ; x 0 时, x x x y x 1 ( ) 1 = (ln( − )) = − − = , x 0 时, x x 1 (ln | |) = . 例 6 y = ln sin( 2x) ,求 y . 解 sin( 2 ) 2cos(2 ) cos(2 ) sin( 2 ) 2 x x x x y = = . 四、 隐函数微分法 若可微函数 y = y(x) 满足方程 F(x, y) = 0 ,则其导数可以从 F(x, y) = 0 dx d 求出.一个方程 F(x, y) = 0 何时能唯一决定一个可微函数 y = y(x) ,留待日后解决,现在我们通常假定能唯一决 定一个可微函数,考虑如何求出导函数问题

《数学分析》上册教案 第五章导数与微分 海南大学数学系 例7+少=,求过点,)0≠0)的切线方程 解对方程产+少2=a求导,心中记住少=)是x的函数,得 2x+2y·y'=0 在)点上,)=-点 %,过(x)切线方程为 %受-刘 xx+%6=x02+%2 即+%6=a2 五、对数微分法我们结合例子研究对数微分法 x 例8yx-。a>0 ,求y 解甬数定义装0和a,国,取对教hy-国-a两边对y-求导, y31112x-3a 采用隐函数微分法,得少2x2x-a2xx-0),所以 例9y=,u=x),v=x),求y 解取对数,得hy=h“,两边求导,得y =hu+pd y-y(W+v.hu)-r(Wtv.hu) 如y=x,y=x'(1+hx). 六、双曲函数及其反函数之导数 y=shx=(e'-e) y=chx=(e*+e") =h-路
《数学分析》上册教案 第五章 导数与微分 海南大学数学系 8 例 7 2 2 2 x + y = a ,求过点 ( , ) 0 0 x y ( 0) y0 的切线方程. 解 对方程 2 2 2 x + y = a 求导,心中记住 y = y(x) 是 x 的函数,得 2x + 2y y = 0 , y x y(x) = − , 在 ( , ) 0 0 x y 点上, 0 0 0 ( ) y x y x = − ,过 ( , ) 0 0 x y 切线方程为 ( ) 0 0 0 0 x x y x y − y = − − , 2 0 2 0 0 0 xx + yy = x + y , 即 2 xx0 + yy0 = a . 五、 对数微分法 我们结合例子研究对数微分法 例 8 ( 0) 3 − = a x a x y ,求 y . 解 函数定义域 (−,0) 和 (a,+) ,取对数 ln | | 2 1 ln | | 2 3 ln y = x − x − a ,两边对 y = y(x) 求导, 采用隐函数微分法,得 2 ( ) 1 2 3 2 1 1 2 3 x x a x a y x x a y − − = − = − ,所以 x a x x x a x a y − − − = 3 2 ( ) 2 3 . 例 9 v y = u , u = u(x) , v = v(x) ,求 y . 解 取对数,得 ln y = v ln u ,两边求导,得 u u v u v y y = + 1 ln , ( ln ) ( v ln u ) u vu v u u u vu y y v + + = = . 如 x y = x , y x (1 ln x) x = + . 六、双曲函数及其反函数之导数 ( ) 2 1 x x y sh x e e − = = − , ( ) 2 1 x x y ch x e e − = = + , ch x sh x y = th x =

《数学分析》上册教案 第五章导数与微分 海南大学数学系 y-cthx=chx shx 性质ch2x-shx=1 ch'x+sh'x=ch2x sh2x=2shx.chx sh(x±y)=shx·chy±chx·shy cx±y)=chx·chy±shx.shy 1-th'x=chx 1 1-cthix= shx+chx=e* [cos0+isin 0=ei chx-shx=e 由(cos0-isin=eo (shx)'=chx (chx)'=shx (thx)= 1 反双曲函数 Arshx=In(x+1+x) 1 (4hy=hy=hxo动可+ 4rchx不是单值函数,可选一个分支来研究 =分 (Arthx)= 1 小结 一、基本求导法则 l.(u±yy=; 2.(uv)=uv+uv',(cuy=cu';
《数学分析》上册教案 第五章 导数与微分 海南大学数学系 9 sh x ch x y = cth x = 性质 1 2 2 ch x − sh x = ch x sh x ch2x 2 2 + = sh 2x = 2sh x ch x sh(x y) = sh x ch y ch x sh y ch(x y) = ch x ch y sh x sh y ch x th x 2 2 1 1− = sh x cth x 2 2 1 1− = − x x ch x sh x e sh x ch x e − − = + = 由 − = + = − i i i e i e cos sin cos sin (sh x) = ch x (ch x) = sh x ch x th x 2 1 ( ) = 反双曲函数 ln( 1 ) 2 Arsh x = x + + x 2 1 1 [ ] 1 ( ) 1 ( ) ch Arsh x x sh y y Arsh x Arsh x + = = = = Arch x 不是单值函数,可选一个分支来研究 x x Arth x − + = 1 1 ln 2 1 2 1 1 ( ) x Arth x − = 小结 一、 基本求导法则 1. (u v)'= u'v' ; 2. (uv)'= u'v + uv' , (cu)'= cu' ;

《数学分析》上册教案 第五章导数与微分 海南大学数学系 3.白=”白= 4.反函数导数少-少.d山 dx du dx 二、基本初等函数导数公式 1.(cy=0: 2.(x“y=aa(aeR); 3.(sin x)'=cosx,(cosx)'=-sin x 4.(tan)=sec2x,(cot)=-cscx, (secx)'=secx-tanx,(cscx)=-cscx-crgx: 5.(a'y=a'lna,(e'y=e"; 1 1 1 7.(ay-京as= v-x (arctan xy-(arecotx-
《数学分析》上册教案 第五章 导数与微分 海南大学数学系 10 3. 2 ' ' ( )' v u v uv v u − = , 2 1 )' 1 ( v v = − ; 4. 反函数导数 dx du du dy dx dy = . 二、基本初等函数导数公式 1.(c)'= 0 ; 2. 1 ( )' − = x x ( R) ; 3.(sin x)'= cos x , (cos x)'= −sin x ; 4. x 2 (tan)' = sec , x 2 (cot)' = −csc , (sec x)'= sec x tan x , (csc x)'= −csc x ctgx ; 5. a a a x x ( )'= ln , x x (e )'= e ; 6. x a x a ln 1 (log )'= , x x 1 (ln )'= ; 7. 2 1 1 (arcsin )' x x − = , 2 1 1 (arccos )' x x − = − ; 2 1 1 (arctan )' x x + = , 2 1 1 ( cot )' x arc x + = −