
《数学分析》教案 第七章实数的完备性 海南大学数学系 第七章实数的完备性 §1实数完备性的等价命题 一、问题提出 定理11(确界原理)非空有上(下)界的数集必有上(下)确界. 确界存在定理(定理1.1)揭示了实数的连续性和实数的完备性.与之等价的还有五大命题 这就是以下的定理1.2至定理1.6. 定理1.2(单调有界定理)任何单调有界数列必定收敛. 定理1.3(区间套定理)设4,6,》为一区间套: [a,8 ]3[am.b12. 2照(6-4,)-0 则存在唯一一点∈[a点,],n-12,. 定理1.4(有限覆盖定理)设H-(化)是闭区间a,b]的一个无限开覆盖,即a,b] 中每一点都含于H中至少一个开区间(出8)内.则在H中必存在有限个开区间,它们构成a,b] 的一个有限开覆盖. 定理1.5(聚点定理)直线上的任一有界无限点集S至少有一个聚点片即在的任意小邻 域内都含有S中无限多个点(本身可以属于S,也可以不属于S). 定理1.6(柯西准则)数列0,收敛的充要条件是:Y>0,3NeN,只要m>,恒 有a“,K8.(后者又称为柯西(Cauchy)条件,满足柯西条件的数列又称为柯西列,或基 本列.) 这些定理构成极限理论的基础.我们不仅要正确理解这六大定理的含义,更重要的还要学会 怎样用它们去证明别的命题.下面通过证明它们之间的等价性,使大家熟悉使用这些理论工具, 下图中有三种不同的箭头,其含义如下: ◆,(1)~(3)基本要求类 (4)(7)阅读参考类
《数学分析》教案 第七章 实数的完备性 海南大学数学系 1 第七章 实数的完备性 §1 实数完备性的等价命题 一、问题提出 定理 1.1(确界原理)非空有上(下)界的数集必有上(下)确界. 确界存在定理(定理 1.1)揭示了实数的连续性和实数的完备性. 与之等价的还有五大命题, 这就是以下的定理 1.2 至定理 1.6. 定理 1.2 (单调有界定理) 任何单调有界数列必定收敛. 定理 1.3 (区间套定理) 设 为一区间套: . 则存在唯一一点 定理 1.4 (有限覆盖定理) 设 是闭区间 的一个无限开覆盖,即 中每一点都含于 中至少一个开区间 内.则在 中必存在有限个开区间,它们构成 的一个有限开覆盖. 定理 1.5 (聚点定理) 直线上的任一有界无限点集 至少有一个聚点 ,即在 的任意小邻 域内都含有 中无限多个点( 本身可以属于 ,也可以不属于 ). 定理 1.6 (柯西准则) 数列 收敛的充要条件是: ,只要 恒 有 .(后者又称为柯西(Cauchy)条件,满足柯西条件的数列又称为柯西列,或基 本列.) 这些定理构成极限理论的基础.我们不仅要正确理解这六大定理的含义,更重要的还要学会 怎样用它们去证明别的命题.下面通过证明它们之间的等价性,使大家熟悉使用这些理论工具. 下图中有三种不同的箭头,其含义如下: : (1)~(3) 基本要求类 : (4)~(7) 阅读参考类
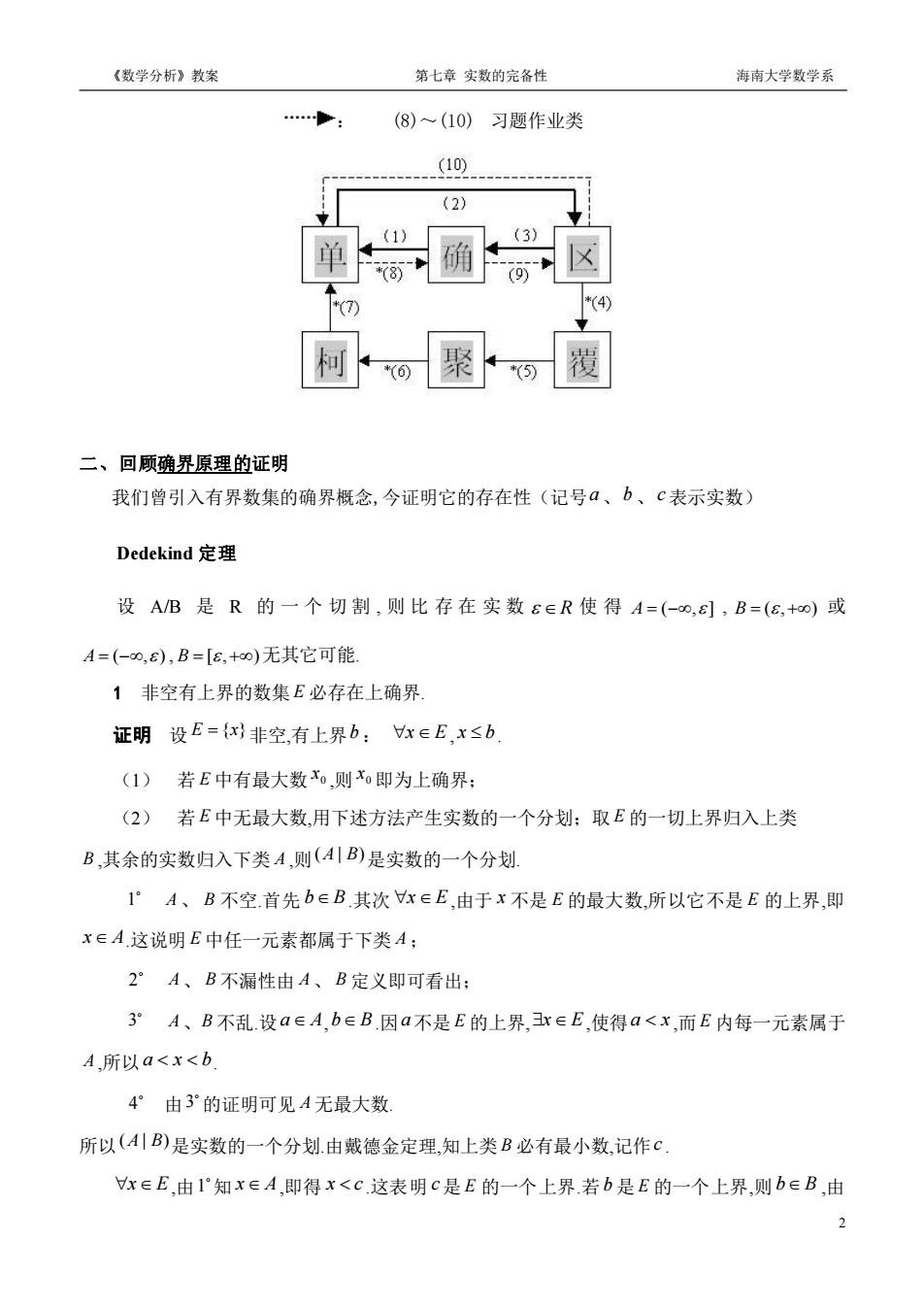
《数学分析》教案 第七章实数的完备性 海南大学数学系 (8)~(10)习题作业类 .-(10 (2 柯o聚o覆 二、回顾确界原理的证明 我们曾引入有界数集的确界概念,今证明它的存在性(记号a、b、c表示实数) Dedekind定理 设AB是R的一个切割,则比存在实数E∈R使得A=(-o,),B=(8,+o)或 A=(-o,s),B=【8,+o)无其它可能. 1非空有上界的数集£必存在上确界 证明设E={x非空,有上界b:x∈E,x≤b (1)若E中有最大数x,则x即为上确界: (2)若E中无最大数,用下述方法产生实数的一个分划:取E的一切上界归入上类 B,其余的实数归入下类A,则(4B)是实数的一个分划! 1°A、B不空首先bEB其次r∈E,由于x不是E的最大数,所以它不是E的上界,即 xEA这说明E中任一元素都属于下类A; 2°A、B不漏性由A、B定义即可看出: 3°A、B不乱.设aeA,b∈B.因a不是E的上界,3r∈E,使得a<x,而E内每一元素属于 A,所以a<x<b 4°由3°的证明可见A无最大数 所以(4川B)是实数的一个分划.由戴德金定理,知上类B必有最小数,记作C x∈E,由1“知x∈A,即得x<c这表明c是E的一个上界.若b是E的一个上界,则b∈B,由 2
《数学分析》教案 第七章 实数的完备性 海南大学数学系 2 : (8)~(10) 习题作业类 二、回顾确界原理的证明 我们曾引入有界数集的确界概念,今证明它的存在性(记号 a、b 、c 表示实数) Dedekind 定理 设 A/B 是 R 的 一 个 切 割 , 则 比 存 在 实 数 R 使 得 A = − ( , ] , B = + ( , ) 或 A = − ( , ) , B = + [ , ) 无其它可能. 1 非空有上界的数集 E 必存在上确界. 证明 设 E = {x} 非空,有上界 b : x E, x b. (1) 若 E 中有最大数 0 x ,则 0 x 即为上确界; (2) 若 E 中无最大数,用下述方法产生实数的一个分划;取 E 的一切上界归入上类 B ,其余的实数归入下类 A ,则 (A | B) 是实数的一个分划. 1 A、 B 不空.首先 bB.其次 x E,由于 x 不是 E 的最大数,所以它不是 E 的上界,即 x A.这说明 E 中任一元素都属于下类 A ; 2 A、 B 不漏性由 A 、 B 定义即可看出; 3 A、B 不乱.设 a A,bB.因 a 不是 E 的上界,xE,使得 a x ,而 E 内每一元素属于 A ,所以 a x b. 4 由 3 的证明可见 A 无最大数. 所以 (A | B) 是实数的一个分划.由戴德金定理,知上类 B 必有最小数,记作 c . x E,由 1 知 x A,即得 x c .这表明 c 是 E 的一个上界.若 b 是 E 的一个上界,则 bB ,由

《数学分析》教案 第七章实数的完备性 海南大学数学系 此得c≤b,所以c是上界中最小的,由上确界定义,c为集合E的上确界,记作c=spE 推论非空的有下界的集合必有下确界 事实上,设集合E=有下界b,则非空集合E=x-x∈B有上界-b,利用集合E'上确界 的存在性,即可得出集合£的下确界存在 定理1解决了非空有上界集合的上确界存在性问题,我们可以利用上确界的存在性,得出我们 所研究的某一类量(如弧长)的存在性 若全序集中任一非空有上界的集合必有上确界,我们称该全序集是完备的定理1刻划了实数 集是完备的 例1证明实数空间满足阿基米德原理 证明∀b>a>0,要证存在自然数n使a>b.假设结论不成立,即 a≤b,(m=l,2.) 则数集E={na}有上界b,因此有上确界c,使na≤c(m=l,2,.),也就有 (n+I)a≤c(n=,2,.),或na≤c-a(m=l2,.).这表明c-a是集合E的上界与c是上确 界矛盾.所以总存在自然数n,使na>b 三、等价命题证明 下面来完成(1)(7)的证明. (一)用确界定理证明单调有界定理 设,单调上升,即名≤名≤名≤.≤x≤.有上界,即3M,使得≤M 考虑集合E=化,nEN,它非空,有界,定理2推出它有上确界,记为a=即我们验证 a=lim x 6>0,由上确界的性质,3N,使得a-8N时,由序列单调上升得a-8<xw≤x。, 再由上确界定义,x≤a<a+6,有a-6<x,<a+,即k,-d<6,也就是说血x=a=即, 同理可证若伍,}单调下降,有下界,也存在极限且血。,=赋无 若集合E无上界,记作supE=+0:若集合E无下界,记作fE=+o,这样一来定理2证明了 的单调上升(下降)有上界(下界)的序列,},必有极限即,矿)的定理现在有了严格的 理论基础了且对单调上升(下降)序列x},总有
《数学分析》教案 第七章 实数的完备性 海南大学数学系 3 此得 c b ,所以 c 是上界中最小的,由上确界定义, c 为集合 E 的上确界,记作 c = sup E . 推论 非空的有下界的集合必有下确界. 事实上,设集合 E = {x} 有下界 b ,则非空集合 E' = {x | −x E} 有上界−b ,利用集合 E' 上确界 的存在性,即可得出集合 E 的下确界存在. 定理 1 解决了非空有上界集合的上确界存在性问题,我们可以利用上确界的存在性,得出我们 所研究的某一类量(如弧长)的存在性. 若全序集中任一非空有上界的集合必有上确界,我们称该全序集是完备的.定理 1 刻划了实数 集是完备的. 例1 证明实数空间满足阿基米德原理. 证明 b a 0,要证存在自然数 n 使 na b .假设结论不成立,即 na b, (n = 1,2,), 则数集 E = {na} 有上界 b , 因此有上确界 c , 使 na c (n = 1,2,), 也就有 (n +1)a c (n = 1,2,),或 na c − a (n = 1,2,).这表明 c − a 是集合 E 的上界,与 c 是上确 界矛盾.所以总存在自然数 n ,使 na b . 三、等价命题证明 下面来完成(1)~(7)的证明. (一) 用确界定理证明单调有界定理 设 { }n x 单调上升,即 x1 x2 x3 xn ,有上界,即 M ,使得 xn M . 考虑集合 E {x | n N} = n ,它非空,有界,定理 2 推出它有上确界,记为 n n N a x = sup .我们验证 n n a x → = lim . 0 ,由上确界的性质, N ,使得 N a − x ,当 n N 时,由序列单调上升得 N n a − x x , 再由上确界定义, x a a + n ,有 a − x a + n ,即 x − a n ,也就是说 n n N n n x a x → lim = = sup . 同理可证若 { }n x 单调下降,有下界,也存在极限,且 n n N n n x x → lim = inf . 若集合 E 无上界,记作 sup E = + ;若集合 E 无下界,记作 inf E = + ,这样一来,定理 2 证明了 的单调上升(下降)有上界(下界)的序列 { }n x ,必有极限 sup (inf ) n x N n x N x x 的定理现在有了严格的 理论基础了.且对单调上升(下降)序列 { }n x ,总有

《数学分析》教案 第七章实数的完备性 海南大学数学系 mxm=spx。(nfxa) (仁)用单调有界定理证明区间套定理 由假设(1)知,序列a,}单调上升,有上界6:序列b,}单调下降,有下界4.因而有 lman=c1mb,=c3an≤G≤c2≤bn 再由假设(2)知 lim (b-a)=c2-C=0 记9=G2=C.从而有 lim d =c=lim b 若还有c满足a,≤c≤b,令n→切,得c=c,故c是一切ab,小的唯一公共点.证毕, 这个定理称为区间套定理.关于定理的条件我们作两点说明: (1)要求[a,b,]是有界闭区间的这个条件是重要的.若区间是开的,则定理不一定成立, 如 a6,)=0, 显然有@,c0为,但iQ=4 如果开区间套是严格包含:a,03NeN,当n>N时,恒 有 [a,b]cU(点 用区间套定理证明其他命题时,最后常会用到这个推论
《数学分析》教案 第七章 实数的完备性 海南大学数学系 4 lim sup (inf ) n x N n x N n n x x x →+ = . (二) 用单调有界定理证明区间套定理 由假设(1)知,序列 { }n a 单调上升,有上界 1 b ;序列 { }n b 单调下降,有下界 1 a .因而有 1 lim a c n n = →+ , 2 lim b c n n = →+ . n bn a c1 c2 . 再由假设(2)知 lim ( − ) = 2 − 1 = 0 →+ b a c c n n n , 记 c = c = c 1 2 . 从而有 n n n n a c b →+ →+ lim = = lim . 若还有 * c 满足 n bn a c * ,令 n → +,得 c = c * .故 c 是一切 [ , ] an bn 的唯一公共点.证毕. 这个定理称为区间套定理.关于定理的条件我们作两点说明: (1) 要求 [ , ] an bn 是有界闭区间的这个条件是重要的.若区间是开的,则定理不一定成立. 如 ) 1 ( , ) (0, n an bn = . 显然有 ) 1 ) (0, 1 1 (0, n n + , 但 = + = ) 1 (0, n 1 n . 如果开区间套是严格包含: an an+1 bn+1 bn ,这时定理的结论还是成立的. (2)若 [ , ] [ , ] an+1 bn+1 an bn (n = 1,2,),但 lim ( − ) 0 →+ n n n b a ,此时仍有 1 lim a c n n = →+ , 2 lim b c n n = →+ ,但 1 2 c c ,于是对任意的 c , 1 2 c c c ,都有 [ , ] 1 n n n c a b + = . 全序集中任一区间长趋于零的区间套有非空交集,则称该全序集是完备的,定理 3 刻划实 数集是完备的(这里完备定义与上段完备定义是等价的).定理 3 也给出通过逐步缩小搜索范围, 找出所求点的一种方法. 推论 设 为一区间套, .则 当 时,恒 有 . 用区间套定理证明其他命题时,最后常会用到这个推论.

《数学分析》教案 第七章实数的完备性 海南大学数学系 例2序列x}由下列各式 =0.5=6,=a-34同 2 所确定(见下图).证明极限血存在,并求此极限。 内巧4→x 证明当a=b时,。=0,故血,=a 当a≠b时,若取an=min),bn=max1,xn),(n=l,2,.) 则由条件,显然可得一串区间套: [a,b]c[a,b](n=12,.) 由已知条件 -+-,=-) 2 于是 6-a,xa-,上l-x上1x-x ==2是l-x卡21b-a0a→4m 由区间套定理,存在c满足:血a,=c-血6,注意到,e口,b】,所以m=c 下面来求.由或-令”=23k-1得一串等式 -名=-,-), x-=-3-x) x-=-2-)
《数学分析》教案 第七章 实数的完备性 海南大学数学系 5 例2 序列 { }n x 由下列各式 x1 = a , x2 = b , 2 −1 + −2 = n n n x x x (n = 3,4,) 所确定(见下图).证明极限 n n x →+ lim 存在,并求此极限. 1 x 3 x 5 x 4 x 2 x x 证明 当 a = b 时, xn = a ,故 xn a n = →+ lim . 当 a b 时,若取 min( , ) n n 1 n a x x = + , max( , ) n n 1 n b x x = + , (n = 1,2,). 则由条件,显然可得一串区间套: [ , ] [ , ] an+1 bn+1 an bn (n = 1,2,). 由已知条件 ( ) 2 1 2 1 1 1 − − + − = − − + − = n n n n n n n x x x x x x x , 于是 | | 0 ( ), 2 1 | | 2 1 | | 2 1 | | 2 1 | | 1 2 1 1 1 1 2 1 2 = = − = − → → + − = − = − = − − − + − − − x x b a n b a x x x x x x n n n n n n n n n n 由区间套定理,存在 c 满足: n n n n a c b →+ →+ lim = = lim .注意到 [ , ] n an bn x ,所以 x c n n = →+ lim . 下面来求 c .由 ( ) 2 1 n+1 − n = − n − n−1 x x x x ,令 n = 2,3,,k −1 得一串等式: ( ) 2 1 3 2 2 1 x − x = − x − x ; ( ) 2 1 4 3 3 2 x − x = − x − x ; ( ) 2 1 k − k−1 = − k−1 − k−2 x x x x

《数学分析》教案 第七章实数的完备性 海南大学数学系 将它们相加,得-名一,令k→m,得-5=-c- 所以 c=++2 (三)用区间套定理证明确界原理 证明思想:构造一个区间套,使其公共点即为数集的上确界. 设58,有上界以,取0e8令[o,1-0,92a1+,再 侣营是, 如此无限进行下去,得一区间套【a,bn}→3n∈[aa,b1,8=1,2. 可证9~卿心,因如恒为9的上界,且职b”,故红∈8,必有 x≤bn台x≤门 这说明7是的上界:又因职0”故Ve>0.30>18,而都不是的上界因此 ”8更不是8的上界.所以”=即8成立。【证毕] *(四)用区间套定理证明有限覆盖定理 设H为闭区间[a,b]的一个无限开覆盖.反证法假设: “[a,b]不能用:中有限个开区间来覆盖” 对a,b]采用逐次二等分法构造区间套(a,4]》,[a,6,]的选择法则:取“不能用H中 有限个开区间来覆盖”的那一半. 由区间套定理,3[4,4n-12,. 导出矛盾:“a,b](出列eH,使(a,小 记8=m(上化分-月〉0,由[推论],当足够大时, [a.,b.]cU(点s)c(g8) 这表示[a,8]用H中一个开区间(出B)就能覆盖,与其选择法则相违背.所以[a,b]必能 用H中有限个开区间来覆盖. 6
《数学分析》教案 第七章 实数的完备性 海南大学数学系 6 将它们相加,得 ( ) 2 1 2 1 1 x x x x k − = − k− − ,令 k →+,得 ( ) 2 1 2 1 c − x = − c − x 所以 ( 2 ) 3 1 3 2 3 1 c = x1 + x2 = a + b . (三) 用区间套定理证明确界原理 证明思想:构造一个区间套,使其公共点即为数集的上确界. 设 , 有上界 .取 ; ,再令 如此无限进行下去,得一区间套 . 可证 :因 恒为 的上界,且 ,故 ,必有 , 这说明 是 的上界;又因 ,故 ,而 都不是 的上界,因此 更不是 的上界.所以 成立. [ 证毕 ] *(四) 用区间套定理证明有限覆盖定理 设 为闭区间 的一个无限开覆盖.反证法假设: “ 不能用 中有限个开区间来覆盖”. 对 采用逐次二等分法构造区间套 , 的选择法则:取“不能用 中 有限个开区间来覆盖”的那一半. 由区间套定理, . 导出矛盾: 使 记 由[推论],当 足够大时, 这表示 用 中一个开区间 就能覆盖,与其选择法则相违背.所以 必能 用 中有限个开区间来覆盖.

《数学分析》教案 第七章实数的完备性 海南大学数学系 说明当[a,b]改为(a,b)时,或者H不是开覆盖时,有限覆盖定理的结论不一定成立. 例如: H是开区间(0,1)的一个无限开覆盖,但不能由此产生(0,1)的有限覆盖 H是[0,2]的一个无限覆盖,但不是开覆盖,由此也无法产生0,2]的有限覆盖 *(五)用有限覆盖定理证明聚点定理 设8为实轴上的有界无限点集,并设8c[-M,M]. ”由反证法假设来构造[-M,M]的一个无限开覆盖:若8有聚点乌,则 [-M,M].现反设[-M,M]中任一点都不是S的聚点,即xeM,M)34>0在 U(x:)内至多只有x∈8.这样。 H-{Ux,&‖x∈【M,M]) 就是[-M,M]的一个无限开覆盖. 2”用有限覆盖定理导出矛盾:据定理9,存在 产={Ux:i=1,2.,N}cH. 户为[-M,M]的一个有限开覆盖(同时也覆盖了8),由假设,:4内至多只有 4∈8一产所属N个邻域内至多只有,.,w属于8(即产只覆盖了8中有限个点).这 与产覆盖了全部S中无限多个点相矛盾. 所以,有界无限点集$必定至少有一个聚点。[证毕] 推论(致密性定理)有界数列必有收敛子列.即若(a,为有界数列,则a,c(a,)使 有 即4之
《数学分析》教案 第七章 实数的完备性 海南大学数学系 7 说明 当 改为 时,或者 不是开覆盖时,有限覆盖定理的结论不一定成立. 例如: 1) . 是开区间 的一个无限开覆盖,但不能由此产生 的有限覆盖. 2) . 是 的一个无限覆盖,但不是开覆盖,由此也无法产生 的有限覆盖. * (五) 用有限覆盖定理证明聚点定理 设 为实轴上的有界无限点集,并设 . 由反证法假设来构造 的一个无限开覆盖:若 有聚点 ,则 .现反设 中任一点都不是 的聚点,即 在 内至多只有 .这样, 就是 的一个无限开覆盖. 用有限覆盖定理导出矛盾:据定理 9,存在 为 的一个有限开覆盖(同时也覆盖了 ).由假设, 内至多只有 所属 个邻域内至多只有 属于 (即 只覆盖了 中有限个点).这 与 覆盖了全部 中无限多个点相矛盾. 所以,有界无限点集 必定至少有一个聚点.[证毕] 推论(致密性定理) 有界数列必有收敛子列.即若 为有界数列,则 使 有 .

《数学分析》教案 第七章实数的完备性 海南大学数学系 子列a的极限称为原数列(a,}的一个极限点,或称聚点 注数列(a:J的聚点与一般点集S的聚点,含义稍有不同.数列的聚点定义为: “6>0,在认片内含有a)中无限多个项,则为a)的一个聚点.”在此意义下, 对于数列 a1分1京5京.1 它有两个收数子列:41和受,-12.它们的模限有-1和奇-0我是6的 两个聚点. 证a,有界,则存在数,片使得≤a,≤乃对m成立 新川三等粉为6学,川则英中整有-个省行数到以指无资李原 记为丙1,再指丙1二等分为,.卢”川,同群其中至少有一个含有数列 2 2 a.的无穷多项,把它记为山,.一直进行这样的步骤,得到一闭区间套x.》,其中 每一个[x。y]中都含有数列a的无穷多项,且满足: )3,]x2,y]与.xy]2. ②m6-)=m2-产=0 则由闭区间套定理,5使得血a,=血6.=专 下证a,中必有一子列收敛于实数5 先在西]中选取a,}的某一项,记为a,因]中含有a,}中的无穷多项,可选取位于 a后的某一项,记为,%>川.继续上述步骤,选取∈[x,]后,因为小中含有无 穷多项,可选取位于a,后的某一项,记为且”1>m,这样我们就得到a,}的一个子列o,} 满足≤0≤4,k=12 由两边夹定理即得血0,“5
《数学分析》教案 第七章 实数的完备性 海南大学数学系 8 子列 的极限 称为原数列 的一个极限点,或称聚点 注 数列 的聚点与一般点集 的聚点,含义稍有不同.数列的聚点定义为: “ ,在 内含有 中无限多个项,则 为 的一个聚点.”在此意义下, 对于数列 它有两个收敛子列: 和 , .它们的极限 和 就是 的 两个聚点. 证 { }n a 有界,则存在数 1 1 x , y 使得 1 1 x a y n 对 n 成立. 将 [ , ] 1 1 x y 二等分为 ] 2 [ , 1 1 1 x y x + 、 , ] 2 [ 1 1 1 y x + y ,则其中必有一个含有数列 { }n a 的无穷多项, 记为 [ , ] 2 2 x y ;再将 [ , ] 2 2 x y 二等分为 ] 2 [ , 2 2 2 x y x + 、 , ] 2 [ 2 2 2 y x + y ,同样其中至少有一个含有数列 { }n a 的无穷多项,把它记为 [ , ] 3 3 x y ,.一直进行这样的步骤,得到一闭区间套 {[ , ]} n n x y ,其中 每一个 [ , ] n n x y 中都含有数列 { }n a 的无穷多项,且满足: ⑴ [ , ] 1 1 x y [ , ] 2 2 x y [ , ] n n x y . ⑵ 1 1 1 lim( ) lim 0 2 n n n n n y x y x → → − − − = = 则由闭区间套定理, 使得 = → n n lim a = → n n lim b 下证 { }n a 中必有一子列收敛于实数 先在 [ , ] 1 1 x y 中选取 { }n a 的某一项,记为 n1 a ,因 [ , ] 2 2 x y 中含有 { }n a 中的无穷多项,可选取位于 n1 a 后的某一项,记为 n2 a , n2 n1 .继续上述步骤,选取 nk a [ , ] k k x y 后,因为 [ , ] k+1 k+1 x y 中含有无 穷多项,可选取位于 nk a 后的某一项,记为 k 1 n a + 且 nk+1 nk ,这样我们就得到 { }n a 的一个子列 { } nk a 满足 k n k x a y k , k = 1,2, 由两边夹定理即得 = → nk n lim a

《数学分析》教案 第七章实数的完备性 海南大学数学系 证明设05么56,用中点9=生 2将,月-分为二,则两个子区间血,和小中至少 有-个含有中无穷多项选出来记为4,1,在其种运一厦用中9品兰将k,】 一分为二,则两个子区间血,9]和,4]中至少有一个含有,}中无穷多项,选出来记为4,6】, 在其中选一项,使得%>川,.最后得一区间套血,6】,满足 [abJ[a.6] xn∈ae,b],nk1>n4 由区间套定理,ma=如6=C,又由于a≤x≤6,有如=C *(六)用聚点定理证明柯西准则 必要性:已知a收敛,设职aa.由定义Ye>03NeN,当mn>N时,有 a.a水2laa水 从而有 la-aslam-al+la,-a03NeN,当m网>N时aa,K.欲证{a,收敛 r.首先证(a,]有界.对于-13eN当”2从,m-从时,有 la,I-lax lslax-a,0,3X(2N以当kmm≥时,有 1a水营-a水f
《数学分析》教案 第七章 实数的完备性 海南大学数学系 9 证明 设 a xn b ,用中点 2 1 a b c + = 将 a,b 一分为二,则两个子区间 1 a, c 和 c ,b 1 中至少 有一个含有 { }n x 中无穷多项,选出来记为 1 1 a ,b ,在其中选一项 n1 x .用中点 2 1 1 2 a b c + = 将 1 1 a ,b 一分为二,则两个子区间 1 2 a , c 和 2 1 c ,b 中至少有一个含有 { }n x 中无穷多项,选出来记为 2 2 a ,b , 在其中选一项 n2 x ,使得 n2 n1 , .最后得一区间套 ak bk , ,满足 ak bk ak bk , , +1 +1 , k k k b a b a 2 − − = , n ak bk nk nk x k , , +1 . 由区间套定理, a b c k k k k = = → → lim lim ,又由于 k n bk a x k ,有 x c nk k = → lim . *(六) 用聚点定理证明柯西准则 必要性: 已知 收敛,设 .由定义, ,当 时,有 . 从而有 . 充分性: 已知条件: 当 时 .欲证 收敛. .首先证 有界.对于 当 时,有 令 ,则有 . .由致密性定理, 存在收敛子列 ,设 . .最后证 ,由条件, 当 时,有 .

《数学分析》教案 第七章实数的完备性 海南大学数学系 于是当n2K(同时有:2k)K)时,就有 la,-ale川a小水字 证“曰”a,}收敛,则存在极限,设a,=a,则G>0,3V,当n>N时有 la,-ak/2-当n,m>N时有la,-a.a-a+la,-ak6 “←”先证有界性,取6=1,则3W,nm>N→a,-amK1 特别地,n>N时|a。-awK1→anai+1 设M=m,laal+,则n,la,M 再由致密性定理知,a,有收敛子列a,设血a,=a e>0,3N,nm>N1→la。-anke/2 aK,k>Kla -aks/2 取N=maNK,N),当n>N时有w12N+l>N ld-aka,-aml+ld-ak6/2+612=6 故ma,=a Cachy列、基本列(满足Cauchy收敛准则的数列) *(七)用柯西准则证明单调有界原理 设(a,)为一递增且有上界y的数列.用反证法(借助柯西准则)可以证明:俏若(a,}无 极限,则可找到一个子列以+0为广义极限,从而与a,}有上界相矛盾.现在来构造这样 的) 对于单调数列a,),柯西条件可改述为:“8>0,WeN,当>N时,满足 口。aw册>W,恒有 amam|≤lan-an0,对一切NN,3>N,使
《数学分析》教案 第七章 实数的完备性 海南大学数学系 10 于是当 (同时有 )时,就有 . 证 “” { }n a 收敛,则存在极限,设 an a n = → lim ,则 0,N ,当 n N 时有 | an − a | / 2 当 n,m N 时有 | a − a || a − a | + | a − a | n m m n “ ”先证有界性,取 =1,则 N , n,m N | an − am | 1 特别地, n N 时 | an − aN+1 |1 | an || aN+1 | +1 设 max{| |,| |, ,| |,| | 1} M = a1 a2 aN aN+1 + ,则 n , | an | M 再由致密性定理知, { }n a 有收敛子列 { } nk a ,设 a a nk k = → lim 0, N1 , 1 n, m N | | / 2 n m a a − K , k K | a − a | / 2 nk 取 max( , ) N = K N1 ,当 n N 时有 1 1 N n N N + + − − + − + = + + | | | | | | / 2 / 2 1 1 a a a a a a n n nN nN 故 an a k = → lim . Cauchy 列、基本列(满足 Cauchy 收敛准则的数列) *(七) 用柯西准则证明单调有界原理 设 为一递增且有上界 M 的数列.用反证法( 借助柯西准则 )可以证明:倘若 无 极限,则可找到一个子列 以 为广义极限,从而与 有上界相矛盾.现在来构造这样 的 . 对于单调数列 ,柯西条件可改述为:“ 当 时,满足 ”.这是因为它同时保证了对一切 ,恒有 . 倘若 不收敛,由上述柯西条件的否定陈述: ,对一切 , ,使