
《数学分析》教案 第七章实数的完备性 海南大学数学系 实数完备性的等价命题 一、问题提出 确界存在定理(定理1.1)揭示了实数的连续性和实数的完备性.与之等价的还有五 大命题,这就是以下的定理1.2至定理1.6. 定理1.2(单调有界定理)任何单调有界数列必定收敛, 定理1.3(区间套定理)设a6,》为一区间套: 1[am,b]p[a1,a],n=1,2. 2知(6,-a))-0 则存在唯一一点[46小,-12. 定理1.4(有限覆盖定理)设H-(心刃是闭区间a,6]的一个无限开覆盖,即 [a,b]中每一点都含于H中至少一个开区间(心列内.则在H中必存在有限个开区间, 它们构成【a,6]的一个有限开覆盖。 定理1.5(聚点定理)直线上的任一有界无限点集S至少有一个聚点户,即在广的 任意小邻域内都含有S中无限多个点(本身可以属于S,也可以不属于S), 定理1.6(何西准则)数列(a,收敛的充要条件是:Y>0,3NeN,只要 m>N,恒有a,-4,K6.《后者又称为柯西(Cauhy)条件,满足柯西条件的 数列又称为柯西列,或基本列。) 这些定理构成极限理论的基础.我们不仅要正确理解这六大定理的含义,更重要的 还要学会怎样用它们去证明别的命题.下面通过证明它们之间的等价性,使大家熟悉使 用这些理论工具. 下图中有三种不同的箭头,其含义如下: ◆,(1)一(3)基本要求类 (4)~(7)阅读参考类 .: (⑧)~(10)习题作业类
《数学分析》教案 第七章 实数的完备性 海南大学数学系 1 实数完备性的等价命题 一、问题提出 确界存在定理(定理 1.1)揭示了实数的连续性和实数的完备性. 与之等价的还有五 大命题,这就是以下的定理 1.2 至定理 1.6. 定理 1.2(单调有界定理) 任何单调有界数列必定收敛. 定理 1.3(区间套定理) 设 为一区间套: . 则存在唯一一点 定理 1.4(有限覆盖定理) 设 是闭区间 的一个无限开覆盖,即 中每一点都含于 中至少一个开区间 内.则在 中必存在有限个开区间, 它们构成 的一个有限开覆盖. 定理 1.5 (聚点定理) 直线上的任一有界无限点集 至少有一个聚点 ,即在 的 任意小邻域内都含有 中无限多个点( 本身可以属于 ,也可以不属于 ). 定理 1.6 (柯西准则) 数列 收敛的充要条件是: ,只要 恒有 .(后者又称为柯西(Cauchy)条件,满足柯西条件的 数列又称为柯西列,或基本列.) 这些定理构成极限理论的基础.我们不仅要正确理解这六大定理的含义,更重要的 还要学会怎样用它们去证明别的命题.下面通过证明它们之间的等价性,使大家熟悉使 用这些理论工具. 下图中有三种不同的箭头,其含义如下: : (1)~(3) 基本要求类 : (4)~(7) 阅读参考类 : (8)~(10) 习题作业类
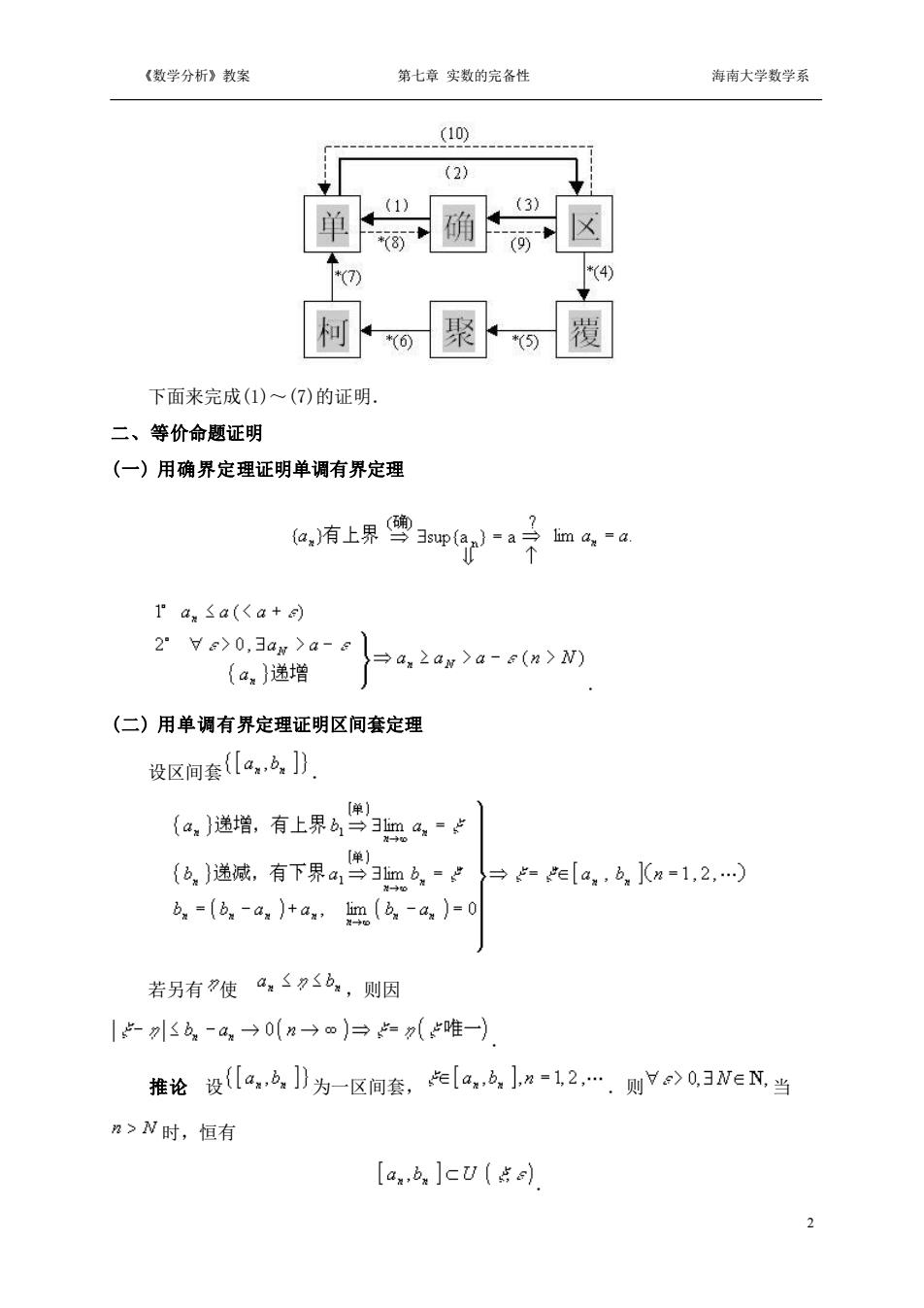
《数学分析》教案 第七章实数的完备性 海南大学数学系 0 (2) 4 柯聚覆 下面来完成(1)~(7)的证明, 二、等价命题证明 (一)用确界定理证明单调有界定理 a,有上果雪3ea子maa 1Pa,≤a(Ka+) 2°Yg>0,3aw>a-6 {a,)递增 =a,2an>a-s(n>N) (二)用单调有界定理证明区间套定理 设区间套(a,4,]) (a,)递增有上果雪职4: 位,)送减有下界婴3胆,-: =e[a,.b,1m=1.2.) 点,=(色,a+a,照a-a)=0 若另有罗使a,≤≤6,则因 |-川b-a→0(n→m〕→(唯一) 推论设a,6]为一区间套,e[a4,]m=12.则Y>03Ne当 ?>N时,恒有 [a.a]cU(点s
《数学分析》教案 第七章 实数的完备性 海南大学数学系 2 下面来完成(1)~(7)的证明. 二、等价命题证明 (一) 用确界定理证明单调有界定理 . (二) 用单调有界定理证明区间套定理 设区间套 . 若另有 使 ,则因 . 推论 设 为一区间套, .则 当 时,恒有 .

《数学分析》教案 第七章实数的完备性 海南大学数学系 用区间套定理证明其他命题时,最后常会用到这个推论 (三)用区间套定理证明确界原理 证明思想构造一个区间套,使其公共点即为数集的上确界。 设S8,有上男M.取而8令[o-(0,自a1+b再令 【a,1-a,1若是的上果 [c1,b1],若c1不是S的上界; 如此无限进行下去,得一区间套【a,b)→3n[a,b如1,”=,2,. 可证习-即8,因,恒为的上界,且,”,故xe8,必有 x≤bn白x≤n 这说明”是8的上界:又因an7,故8>0,3am>n-8,而m都不是8的 上界,因此”8更不是8的上界.所以”=即8成立. *(四)用区间套定理证明有限覆盖定理 设H为闭区间a,b]的一个无限开覆盖。反证法假设: “[a,b]不能用H中有限个开区间来覆盖”· 对a,b]果用逐次二等分法构造区间套a,么】,【a,点]的选择法则:取“不 能用H中有限个开区间来覆盖”的那一半 由区间套定理,3[a,8]”=12.导出矛盾: e[a,b],3(出列eH,使e〔,) 记6”m(六出月)0由[推论],当足够大时, [a,b]cU(点sc(x) 这表示a,6]用H中一个开区间(心)就能覆盖,与其选择法则相违背.所以 [a,b]必能用H中有限个开区间来覆盖
《数学分析》教案 第七章 实数的完备性 海南大学数学系 3 用区间套定理证明其他命题时,最后常会用到这个推论. (三) 用区间套定理证明确界原理 证明思想 构造一个区间套,使其公共点即为数集的上确界. 设 , 有上界 .取 ; ,再令 如此无限进行下去,得一区间套 . 可证 :因 恒为 的上界,且 ,故 ,必有 , 这说明 是 的上界;又因 ,故 ,而 都不是 的 上界,因此 更不是 的上界.所以 成立. *(四) 用区间套定理证明有限覆盖定理 设 为闭区间 的一个无限开覆盖.反证法假设: “ 不能用 中有限个开区间来覆盖”. 对 采用逐次二等分法构造区间套 , 的选择法则:取“不 能用 中有限个开区间来覆盖”的那一半. 由区间套定理, .导出矛盾: 使 . 记 由[推论],当 足够大时, 这表示 用 中一个开区间 就能覆盖,与其选择法则相违背.所以 必能用 中有限个开区间来覆盖

《数学分析》教案 第七章实数的完备性 海南大学数学系 说明当a,b]改为a,b)时,或者H不是开覆盖时,有限覆盖定理的结论不一定 成立例如: H3导 H是开区间(0,1)的一个无限开覆盖,但不能由此产生(0,1)的有限覆盖。 H是[0,2]的一个无限覆盖,但不是开覆盖,由此也无法产生0,2]的有限覆盖 *(五)用有限覆盖定理证明聚点定理 设8为实轴上的有界无限点集,并设8c-M,M] 【”由反证法假设来构造[-M,M]的一个无限开覆盖:若S有聚点之,则 -M,M],现反设[-M,M]中任一点都不是的聚点,即xM,M)34>0, 在x:4)内至多只有xe8.这样, H-{U(x;4川x∈【M,M]) 就是[-M,M]的一个无限开覆盖. 2”用有限覆盖定理导出矛盾:据定理9,存在 产-(U(x;i-1,2.,NcH, 户为-M,M]的一个有限开覆盖(同时也覆盖了S).由假设,川x:4内至多只 有为∈S一丹所属N个邻城内至多只有西.,w属于8(即庄只覆盖了S中有限个 点)·这与户覆盖了全部S中无限多个点相矛盾. 所以,有界无限点集S必定至少有一个聚点,[ 推论(致密性定理)有界数列必有收敛子列.即若{4,}为有界数列,则 引ac(a,使有熙a 子列aJ的极限称为原数列a,小的一个极限点,或称聚点
《数学分析》教案 第七章 实数的完备性 海南大学数学系 4 说明 当 改为 时,或者 不是开覆盖时,有限覆盖定理的结论 不一定 成立.例如: 1) . 是开区间 的一个无限开覆盖,但不能由此产生 的有限覆盖. 2) . 是 的一个无限覆盖,但不是开覆盖,由此也无法产生 的有限覆盖. *(五) 用有限覆盖定理证明聚点定理 设 为实轴上的有界无限点集,并设 . 由反证法假设来构造 的一个无限开覆盖:若 有聚点 ,则 .现反设 中任一点都不是 的聚点,即 在 内至多只有 .这样, 就是 的一个无限开覆盖. 用有限覆盖定理导出矛盾:据定理 9,存在 为 的一个有限开覆盖(同时也覆盖了 ).由假设, 内至多只 有 所属 个邻域内至多只有 属于 (即 只覆盖了 中有限个 点).这与 覆盖了全部 中无限多个点相矛盾. 所以,有界无限点集 必定至少有一个聚点.[ 推论(致密性定理) 有界数列必有收敛子列.即若 为有界数列,则 使有 . 子列 的极限 称为原数列 的一个极限点,或称聚点

《数学分析》教案 第七章实数的完备性 海南大学数学系 数列(4)的聚点与一般点集S的聚点,含义稍有不同.数列的聚点定义为:“H6>0, 在八点)内含有(4)中无限多个项,则为(,)的一个聚点.”在此意义下,对于数 列 o1分1安1安1 1 1 它有两个收敛子列:44-1和“2,”=12.它们的极限片=1和5=0就是 (a,)的两个聚点. *(六)用聚点定理证明柯西准则 柯西准则的必要性容易由数列收敛的定义直接证得。 (已知(a,)收敛,设a,a.由定义,Ye>0日NeN,当A>N时,有 a水管6a水台 从而有 la.-a,Isla,-al+la,-al03NeN,当、m>N时a,K.欲证(a,J收敛 ”.首先证(a,)有界.对于-13eN,当2从,m-从时,有 |a.-aw≤aw-a.K1→la,s am+1 令M=mla川马l.e-川ax+,则有 |a.|≤M,n-1,2,. 2.由致密性定理,(a,}存在收敛子列a,设职a 子.最后证职aa,由条件,V》0,3X(2N当mm2K时,有 la.-a<an -a 于是当n之X(同时有2)K)时,就有
《数学分析》教案 第七章 实数的完备性 海南大学数学系 5 数列 的聚点与一般点集 的聚点,含义稍有不同.数列的聚点定义为:“ , 在 内含有 中无限多个项,则 为 的一个聚点.”在此意义下,对于数 列 它有两个收敛子列: 和 , .它们的极限 和 就是 的两个聚点. *(六) 用聚点定理证明柯西准则 柯西准则的必要性容易由数列收敛的定义直接证得. (已知 收敛,设 .由定义, ,当 时,有 . 从而有 .) 这里只证其充分性. 已知条件: 当 时 .欲证 收敛. .首先证 有界.对于 当 时,有 令 ,则有 . .由致密性定理, 存在收敛子列 ,设 . .最后证 ,由条件, 当 时,有 . 于是当 (同时有 )时,就有

《数学分析》教案 第七章实数的完备性 海南大学数学系 la,-alsla,-ax l+aw-a+ *(七)用柯西准则证明单调有界原理 设{a,)为一递增且有上界M的数列.用反证法(借助柯西准则)可以证明:俏 若(a)无极限,则可找到一个子列a:】以+⊙为广义极限,从而与(a】有上界相矛 盾。现在来构造这样的a,】 对于单调数列{a,),柯西条件可改述为:“e>0,3NeN,当n>W时,满 足aa加>N,恒有 lan-as an-anl0,对一切N∈N,3>N 使 am-aN=aa-aN之0 依次取 2M=1,31>M,使am1a1280: 2W2=m1,3N2>N2,使an2-a1280; 2N-BkH,3nk〉Nk,使akat之80 把它们相加,得到 ans-a12 keo t)4-a 故当 90时,可使“:>M,矛盾.所以单调有界数列(a,)必定有极限。【证 毕] 在以上六个等价命题中,最便于推广至R“中点集的,当属聚点定理与有限覆盖定 理,为加深对聚点概念的认识,下例所讨论的问题是很有意义的 例证明“是点集$的聚点”的以下三个定义互相等价: ①)Y8)0,在U(兰:司内含有5中无限多个点(原始定):
《数学分析》教案 第七章 实数的完备性 海南大学数学系 6 . *(七) 用柯西准则证明单调有界原理 设 为一递增且有上界 M 的数列.用反证法( 借助柯西准则 )可以证明:倘 若 无极限,则可找到一个子列 以 为广义极限,从而与 有上界相矛 盾.现在来构造这样的 . 对于单调数列 ,柯西条件可改述为:“ 当 时,满 足 ”.这是因为它同时保证了对一切 ,恒有 . 倘若 不收敛,由上述柯西条件的否定陈述: ,对一切 , , 使 . 依次取 把它们相加,得到 . 故当 时,可使 ,矛盾.所以单调有界数列 必定有极限.[ 证 毕 ] 在以上六个等价命题中,最便于推广至 中点集的,当属聚点定理与有限覆盖定 理.为加深对聚点概念的认识,下例所讨论的问题是很有意义的. 例 证明“ 是点集 的聚点”的以下三个定义互相等价: (i) 内含有 中无限多个点(原始定义);

《数学分析》教案 第七章实数的完备性 海南大学数学系 ()Y8>0在(点)内含有5中至少一个点: (i)3(x)cS,n*m时x*不,使典五” 证(①)→(i)显然成立 (i)→(ii)由ii),取f=1,3e(六4)n8: 再取m(分“石小,肠er(ns 一般取8m((分D.3x∈(点成ns 由(石的取法,保证(不)C8,本*x(”m),职中 i)→典x~台Y》0,3Ne>N时,必有eU(名,且因 (x)各项互不相同,故八片8)内含有8中无限多个点
《数学分析》教案 第七章 实数的完备性 海南大学数学系 7 (ii) 在 内含有 中至少一个点; (iii) , 时 ,使 . 证 (i) (ii) 显然成立. (ii) (iii) 由(ii),取 , ; 再取 ; . 一般取 ; . 由 的取法,保证 , , . (iii) (i) 时,必有 ,且因 各项互不相同,故 内含有 中无限多个点.