
《数学分析》上册教案 第四章连续函数 海南大学数学系 §3初等函数的连续性 教学章节:第四章连续函数一一§3初等函数的连续性. 教学目标:知道所有初等函数都是在其有定义的区间上连续的函数,并能够加以证明。 教学要求:深刻理解初等函数在其定义的区间上都是连续的,并能应用连续性概念以及连续函数 的性质加以证明,能熟练运用这一结论求初等函数的极限。 教学重点:初等函数的连续性的阐明. 教学难点:初等函数连续性命题的证明。 教学方法:学导式教学 散学过程: 一、复习(关于初等函数) (一)初等函数:由基本初等函数经过有限次四则运算与复合运算所得到的函数 (二)基本初等函数: 常量函数y=C: 幂函数y=x“: 指数函数y=d(a>0,a≠): 对数函数y=log。xa>0,a≠): 三角函数y=sinx,cosx,g,cg; 反三角函数y=arcsinx,arccosx,arcg,arcctgx 二、初等函数的连续 (一)指数函数a、对数函数log。x和幂函数x连续性 引理设a>L,n>1为正整数,则31b>1,使a=b”,由此我们可以定义b=a】 证在区间几,d上考虑函数f)=xeCl,d,且f0=1<a<a=f@). Bolzano-Cauchy第二定理给出beL,a,使a=b, 如果=a,即6”=a,b”=b,由函数f)=x严格单调,推出6=b,即唯一性. 定义者片(以正整数.互素)为正有理数.=r.若9为负有果数.” a9
《数学分析》上册教案 第四章 连续函数 海南大学数学系 1 §3 初等函数的连续性 教学章节:第四章 连续函数——§3 初等函数的连续性. 教学目标:知道所有初等函数都是在其有定义的区间上连续的函数,并能够加以证明. 教学要求:深刻理解初等函数在其定义的区间上都是连续的,并能应用连续性概念以及连续函数 的性质加以证明,能熟练运用这一结论求初等函数的极限. 教学重点:初等函数的连续性的阐明. 教学难点:初等函数连续性命题的证明. 教学方法:学导式教学. 教学过程: 一、 复习(关于初等函数) (一) 初等函数: 由基本初等函数经过有限次四则运算与复合运算所得到的函数. (二) 基本初等函数: 常量函数 y C= ; 幂函数 y x = ; 指数函数 ( 0, 1) x y a a a = ; 对数函数 log ( 0, 1) a y x a a = ; 三角函数 y x x tgx ctgx = sin ,cos , , ; 反三角函数 y x x arctgx arcctgx = arcsin ,arccos , , . 二、初等函数的连续 (一) 指数函数 x a 、对数函数 x a log 和幂函数 x 连续性 引理 设 a 1, n 1 为正整数,则 ! 1 b , 使 n a = b .由此我们可以定义 n b = a . 证 在区间 [1, a] 上考虑函数 f (x) x C[1, a] n = , 且 f (1) 1 a a f (a) n = = . Bolzano-Cauchy 第二定理给出 b [1, a] ,使 n a = b . 如果 n b = a ,即 b a n = , n n b = b ,由函数 n f (x) = x 严格单调,推出 b = b ,即唯一性. 定义 若 n m q = ( m, n 正整数,互素)为正有理数, q n m a = ( a) . 若 q 为负有理数, q q a a − = 1

《数学分析》上册教案 第四章连续函数 海南大学数学系 定义0=1.若2为无理数,定义0一即0,9为有理致 这里需说明sp存在:当9为有理数时,a是单调上升的,即41,>g,所以即存在 最后无论x为有理数还是无理数,都有=即Q,g为有理数 命题f=a严格上升,在(←∞,+∞)上连续, 证明设x0,3N,使得a<1+8),取9,9有理数,使得9<x<:, 4:-g=N,则fx,s+0)sa,f,)2f。-0)2a Is f(x+0)a =a=a<1+ fx。-0)am 所以f(x+0)=f-0)=fxo)=a 指数函数还有性质aa=a5. 命题对数函数y=log∈C(0,+o), 证明x=a'在(-0,+o)上严格上升,连续,其值域为(0,+o),所以其反函数y=log。x在 (0,+)也严格上升,连续 命题幂函数y=x“=eanr∈C(0,+o) 证明它是指数函数和对数函数:=ahx的复合函数,每个函数都连续,它们的复合也 连续。 (二)结论 定理4.12一切基本初等函数都是其定义域上连续函数. 定理4.13任何初等函数都是在其定义区间上的连续函数. 注初等函数的连续区间和间断点:初等函数的间断点是其连续区间的开端点。闭端点 是其单侧连续点
《数学分析》上册教案 第四章 连续函数 海南大学数学系 2 定义 1 0 a = . 若 为无理数,定义 a a q q为有理数 q sup , = . 这里需说明 sup 存在:当 q 为有理数时 , q a 是单调上升的 , 即 q1 q2 时, 1 2 1 1 2 = q −q q q a a a , q2 q1 a a ,所以 sup 存在. 最后无论 x 为有理数还是无理数,都有 a a q q 为有理数 q x x sup , = . 命题 x f (x) = a 严格上升,在 (−,+) 上连续. 证明 设 1 2 x x , 有理数 1 2 q , q ,使得 1 1 2 2 x q q x , 由此 2 2 1 2 1 1 sup sup q x q x q q q q x x a = a a a a = a . ( , ) x0 − + , 0 , N , 使得 N a (1+ ) ,取 1 2 q , q 有理数,使得 1 0 q2 q x , N q q 1 2 − 1 = , 则 2 ( ) ( 0) 0 0 q f x f x + a , 1 ( ) ( 0) 0 0 q f x f x − a , = = + − + − 1 ( 0) ( 0) 1 1 0 0 2 1 1 2 q q N q q a a a a f x f x , 所以 0 ( 0) ( 0) ( ) 0 0 0 x f x + = f x − = f x = a . 指数函数还有性质 1 2 1 2 x x x x a a a + = . 命题 对数函数 y = log x C(0,+ ) a . 证明 y x = a 在 (−,+) 上严格上升,连续,其值域为 (0,+ ) ,所以其反函数 y x a = log 在 (0,+ ) 也严格上升,连续. 命题 幂函数 (0, ) ln y = x = e C + x . 证明 它是指数函数 z e 和对数函数 z =ln x 的复合函数,每个函数都连续,它们的复合也 连续. (二) 结论 定理 4.12 一切基本初等函数都是其定义域上连续函数. 定理 4.13 任何初等函数都是在其定义区间上的连续函数. 注 初等函数的连续区间和间断点: 初等函数的间断点是其连续区间的开端点. 闭端点 是其单侧连续点

《数学分析》上册教案 第四章连续函数 海南大学数学系 例1求通数一二的莲埃区同间和同新点 解D,=[-1,1)U(1,2)U(2,3)U(3,+o) fx)的连续区间为:【-1,1)、(1,2)、(2,3)和(3,+0). 间断点为:x=1,2和3.(f(x)在点x=-1右连续). 三、利用初等函数的连续性可计算极限 求极限的指数法则若)=a>0,▣)=b,则)=a>0 证明如果(,()在点连续,且,)>0,则x)=ea在点连续,补充定义 )=a,)=b,则m)=a 上述段限过程当气=橘-时防度立只要利用安换就行了,例:点+如宁中 我们注意到0+如宁=0+s如马 ,很容易得到它趋向于e,当x→+o时. ∫连续~∫与四可交换: i f(x)=f(x)=f(lim x mf(ox》=f(mp(x》=f(ox》 倒2求h+). x 例3求回 4=-回 (作倒代换1=上) 例5m+g产 解I=m+g)-m+g)eFr=e=e 例6msnr+1-sin 解sn+i-sG=2sar+-Ecos++区 2 2
《数学分析》上册教案 第四章 连续函数 海南大学数学系 3 例 1 求函数 ln 2 1 ( ) − + = x x f x 的连续区间和间断点. 解 = [−1,1) (1, 2 ) ( 2 , 3 ) ( 3, + ). Df f (x) 的连续区间为: [−1,1) 、(1, 2 ) 、( 2 , 3 ) 和 ( 3, + ) . 间断点为: x = 1, 2 和 3. ( f (x) 在点 x = −1 右连续 ) . 三、利用初等函数的连续性可计算极限 求极限的指数法则 若 lim ( ) 0 0 = → u x a x x , v x b x x = → lim ( ) 0 ,则 lim ( ) 0 ( ) 0 = → v x b x x u x a . 证明 如果 u(x), v(x) 在 0 x 点连续,且 u(x0 ) 0 ,则 ( ) ( )ln ( ) ( ) v x v x u x u x = e 在 0 x 点连续,补充定义 u(x0 ) = a , v(x0 ) = b ,则 v x b x x u x = a → ( ) lim ( ) 0 . 上述极限过程当 x0 = +, − 时仍成立,只要利用变换 t x 1 = 就行了,例如: x x x ) 1 lim (1+ sin →+ 中 我们注意到 x x x x x x 1 1 sin 1 sin 1 ) 1 ) (1 sin 1 (1 sin + = + ,很容易得到它趋向于 e ,当 x → + 时. f 连续 f 与 0 lim x→x 可交换: lim ( ) ( ) (lim ) 0 0 0 f x f x f x x→x x→x = = ; lim ( ( )) (lim ( )) ( ( )) 0 0 0 f x f x f x x x x x = = → → . 例 2 求 0 ln(1 ) lim x x → x + . 例 3 求 2 0 ln(1 ) lim cos x x → x + . 例 4 . 1 1 1 1 lim 0 + − − → + x x x x x ( 作倒代换 . ) 1 x t = 例 5 lim (1 ) . sec 0 xctgx x + tgx → 解 I = lim((1 ) ) (lim(1 ) ) . 1 limsec 0 sec 0 0 tgx tgx e e x ctgx x x ctgx x + = + x→ = = → → 例 6 lim (sin x 1 sin x ). x + − →+ 解 sin x +1 − sin x = . 2 1 cos 2 1 2sin x + − x x + + x
《数学分析》上册教案 第四章连续函数 海南大学数学系 s+国s1里s-近-mmT-近-0 2 2 2 .I=0. 作业教材P841,2
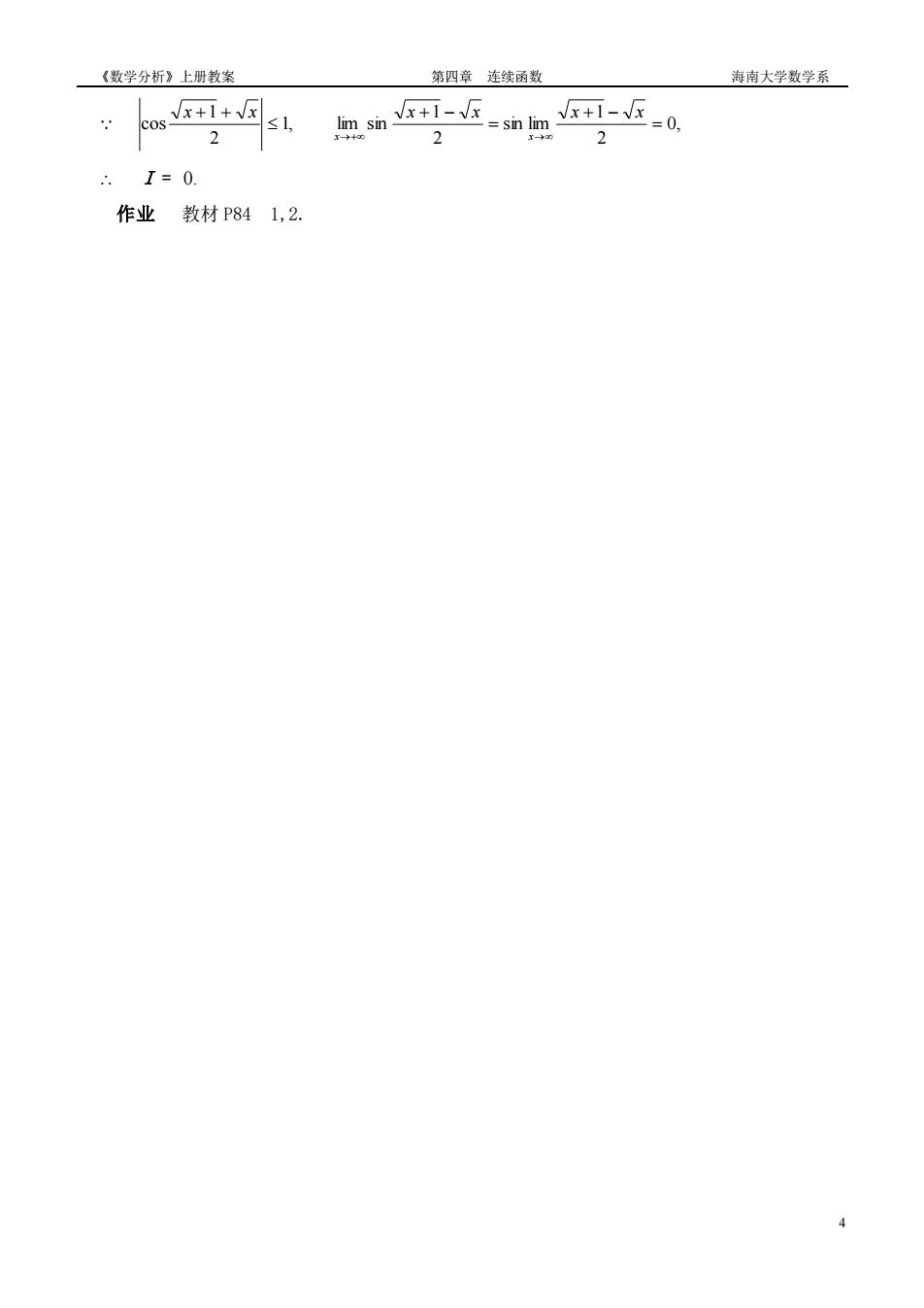
《数学分析》上册教案 第四章 连续函数 海南大学数学系 4 0, 2 1 sin lim 2 1 1, lim sin 2 1 cos = + − = + − + + →+ → x x x x x x x x I = 0. 作业 教材 P84 1,2