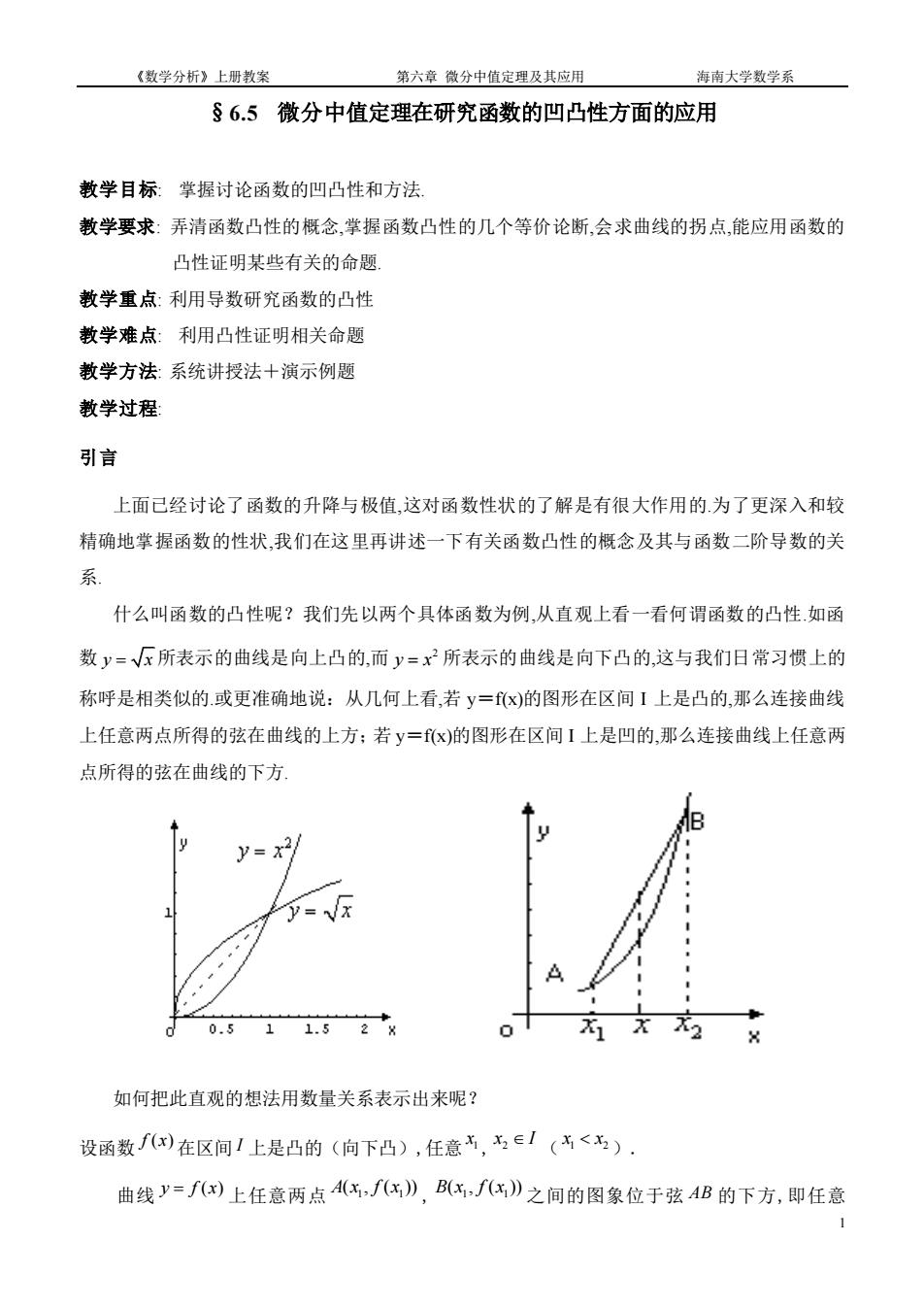
《数学分析》上册教案 第六章微分中值定理及其应用 海南大学数学系 §6.5微分中值定理在研究函数的凹凸性方面的应用 教学目标:掌握讨论函数的凹凸性和方法。 教学要求:弄清函数凸性的概念,掌握函数凸性的几个等价论断,会求曲线的拐点,能应用函数的 凸性证明某些有关的命题。 教学重点:利用导数研究函数的凸性 教学难点:利用凸性证明相关命题 教学方法:系统讲授法十演示例题 教学过程 引言 上面已经讨论了函数的升降与极值,这对函数性状的了解是有很大作用的.为了更深入和较 精确地掌握函数的性状,我们在这里再讲述一下有关函数凸性的概念及其与函数二阶导数的关 什么叫函数的凸性呢?我们先以两个具体函数为例,从直观上看一看何谓函数的凸性如函 数y=√F所表示的曲线是向上凸的,而y=x所表示的曲线是向下凸的,这与我们日常习惯上的 称呼是相类似的或更准确地说:从几何上看,若y=x)的图形在区间I上是凸的,那么连接曲线 上任意两点所得的弦在曲线的上方:若y=x)的图形在区间1上是四的,那么连接曲线上任意两 点所得的弦在曲线的下方 y=x2 =√x 0 0.511.52x 0 如何把此直观的想法用数量关系表示出来呢? 设函数)在区间/上是凸的(向下凸),任意,名∈I(<书) 曲线y=)上任意两点(气,G》,B(x,:》之间的图象位于弦AB的下方,即任意
《数学分析》上册教案 第六章 微分中值定理及其应用 海南大学数学系 1 §6.5 微分中值定理在研究函数的凹凸性方面的应用 教学目标: 掌握讨论函数的凹凸性和方法. 教学要求: 弄清函数凸性的概念,掌握函数凸性的几个等价论断,会求曲线的拐点,能应用函数的 凸性证明某些有关的命题. 教学重点: 利用导数研究函数的凸性 教学难点: 利用凸性证明相关命题 教学方法: 系统讲授法+演示例题 教学过程: 引言 上面已经讨论了函数的升降与极值,这对函数性状的了解是有很大作用的.为了更深入和较 精确地掌握函数的性状,我们在这里再讲述一下有关函数凸性的概念及其与函数二阶导数的关 系. 什么叫函数的凸性呢?我们先以两个具体函数为例,从直观上看一看何谓函数的凸性.如函 数 y x = 所表示的曲线是向上凸的,而 2 y x = 所表示的曲线是向下凸的,这与我们日常习惯上的 称呼是相类似的.或更准确地说:从几何上看,若 y=f(x)的图形在区间 I 上是凸的,那么连接曲线 上任意两点所得的弦在曲线的上方;若 y=f(x)的图形在区间 I 上是凹的,那么连接曲线上任意两 点所得的弦在曲线的下方. 如何把此直观的想法用数量关系表示出来呢? 设函数 f x( ) 在区间 I 上是凸的(向下凸),任意 1 x , 2 x I ( 1 2 x x ). 曲线 y f x = ( ) 上任意两点 1 1 A x f x ( , ( )) , 1 1 B x f x ( , ( )) 之间的图象位于弦 AB 的下方,即任意

《数学分析》上册教案 第六章微分中值定理及其应用 海南大学数学系 x∈(:,),∫()的值小于或等于弦AB在x点的函数值,弦AB的方程 y=f()+) 对任意x∈(:,x)有 )- X2-X ,整理得 X==1- 令3-,则有0<1<且x=:+-%,有5 ,上式可写成 fc+(1-)x]≤f(x)+1-)f(x,) 一、凸函数定义以及与连续性的关系 (一)凸(凹)函数的定义 定义1设函数f为定义在区间1上的函数,若对1上任意两点x、x,和任意实数1e(0,)总 有2x+1-)x)≤fx)+1-)f(x),则称f为I上的凸函数.反之,如果总有 fx+1-)x)2fx)+1-)f(x),则称f为1上的凹函数 注易证:若一f为区间1上的凸函数则f为区间1上的凹函数因此,今后只讨论凸函数的 性质即可 定义2设曲线y=x)在点(x,fx)处有穿过曲线的切线,且在切点近旁,曲线在切线的两 侧分别是严格凸或严格凹的,这时称(x,fx)为曲线y=x)的拐点 必须指出:若(x,f(x)是曲线yf(x)的一个拐点,y=fx)在点x的导数不一定存在,如 y=派在x=0的情形 (二)凸函数的特征 引理f为1上的凸函数一对于I上任意三点:<x,<x总有: ))) (3) X2一X X一X2 fx)严格凸函数一上式严格不等式成立
《数学分析》上册教案 第六章 微分中值定理及其应用 海南大学数学系 2 1 2 x x x ( , ) , f x( ) 的值小于或等于弦 AB 在 x 点的函数值,弦 AB 的方程 2 1 1 1 2 1 ( ) ( ) ( ) ( ) f x f x y x x f x x x − = − + − . 对任意 1 2 x x x ( , ) 有 2 1 1 1 2 1 ( ) ( ) ( ) ( ) ( ) f x f x f x x x f x x x − − + − ,整理得 2 1 1 2 2 1 2 1 ( ) ( ) ( ) x x x x f x f x f x x x x x − − + − − . 令 2 2 1 ( ) x x t x x − = − ,则有 0 1 t ,且 1 2 x tx t x = + − (1 ) ,易得 1 2 1 1 x x t x x − = − − ,上式可写成 1 2 1 2 f tx t x tf x t f x [ (1 ) ] ( ) (1 ) ( ) + − + − . 一、凸函数定义以及与连续性的关系 (一) 凸(凹)函数的定义 定义 1 设函数 f 为定义在区间 I 上的函数,若对 I 上任意两点 1 x 、 2 x 和任意实数 (0,1) 总 有 1 2 1 2 f x x f x f x ( (1 ) ) ( ) (1 ) ( ) + − + − , 则 称 f 为 I 上 的 凸 函 数 . 反 之 , 如果总有 1 2 1 2 f x x f x f x ( (1 ) ) ( ) (1 ) ( ) + − + − ,则称 f 为 I 上的凹函数. 注 易证:若一 f 为区间 I 上的凸函数,则 f 为区间 I 上的凹函数,因此,今后只讨论凸函数的 性质即可. 定义 2 设曲线 y=f(x)在点( 0 0 x f x , ( ) )处有穿过曲线的切线,且在切点近旁,曲线在切线的两 侧分别是严格凸或严格凹的,这时称( 0 0 x f x , ( ) )为曲线 y=f(x)的拐点. 必须指出;若( 0 0 x f x , ( ) )是曲线 y=f(x)的一个拐点,y=f(x)在点 0 x 的导数不一定存在,如 3 y x = 在 x=0 的情形. (二) 凸函数的特征 引理 f 为 I 上的凸函数 对于 I 上任意三点 1 2 3 x x x 总有: 2 1 3 2 2 1 3 2 f x f x ( ) ( ) f x f x ( ) ( ) x x x x − − − − (3) f x( ) 严格凸函数 上式严格不等式成立

《数学分析》上册教案 第六章微分中值定理及其应用 海南大学数学系 证 →记 -元,则0<2<1及名=x+-2店,由f的凸性知 5-点)+-f) fx)≤fx)+(1-)fs)s-x x-x 4) 从而有 (x-x)f(x2)(x-x2)f(x)+(x-x)f(x3) (3-x)f(x)+(:-x)f(x)≤(3-x)f)+(x2-x)f(s) 整理即得(3)式. 七e16<,ae@包名=+0-5,则<西<,=克学 由必要性的推导步骤可逆,从(3)式便得(4)式故∫为凸函数: 同理便知,曲线上首尾相连的线,其斜率是递增的,即,∈/,<。<,有 ()-))-f() - X3一X f)严格凸函数一上式严格不等式成立, 定理设J为开区间1上的凸函数.若0,B]C则J在a,B]上满足利普希茨条件,且J 在1上连续. 证明(证明开区间1上的凸函数必为连续函数)当取定[Q,]c1后,由1为开区间,必可 选取1中的四点a、bcd满足: a<b<a<B<c<d 如图所示,再在[,中任取两点<x.应用引理得到 y=f(x/ 3
《数学分析》上册教案 第六章 微分中值定理及其应用 海南大学数学系 3 证 记 3 2 3 1 x x x x − = − ,则 0 1 及 2 1 3 x x x = + − (1 ) , 由 f 的凸性知 2 1 3 f x f x f x ( ) ( ) (1 ) ( ) + − 3 2 2 1 1 3 3 1 3 1 ( ) ( ) x x x x f x f x x x x x − − = + − − (4) 从而有 3 1 2 3 2 1 2 1 3 ( ) ( ) ( ) ( ) ( ) ( ) x x f x x x f x x x f x − − + − 即 3 2 2 2 1 2 3 2 1 2 1 3 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) x x f x x x f x x x f x x x f x − + − − + − 整理即得 (3) 式. 1 3 x x I , 1 3 ( ) x x , (0,1) 记 2 1 3 x x x = + − (1 ) ,则 1 2 3 x x x , 3 2 2 1 x x x x − = − 由必要性的推导步骤可逆,从 (3) 式便得 (4) 式.故 f 为凸函数. 同理便知,曲线上首尾相连的线,其斜率是递增的,即 1 2 3 x x x I , , , 1 2 3 x x x ,有 2 1 3 1 2 1 3 1 f x f x ( ) ( ) f x f x ( ) ( ) x x x x − − − − f x( ) 严格凸函数 上式严格不等式成立. 定理 设 为开区间 上的凸函数.若 则 在 上满足利普希茨条件,且 在 上连续. 证明 (证明开区间 上的凸函数必为连续函数) 当取定 后,由 为开区间,必可 选取 中的四点 满足: . 如图所示,再在 中任取两点 . 应用引理得到

《数学分析》上册教案 第六章微分中值定理及其应用 海南大学数学系 f)-f(a)sf(x)-f(x)s f(d)-f(o) b-a x-x' d-c @999} 则 四-斗Lreo, x"-x 显然,上述L与[0,刷中的点x无关,故/在1上的每个内闭区间,刷上满足利普希茨 条件. 由此容易推知寸在[,]上连续,再由[,刷在1上的任意性,又可推知J在1上处处连续。 如果「是I上的可导函数,则进一步有: 二、凸函数与导数的关系 定理1(可导函数为凸函数的等价命题)设「为区间1上的可导函数,则下述论断互相等价: (1)f为1上的凸函数:(2)∫为1上的增函数:(3)对1上的任意两点x,x总有 f(x)zf(x)+f(xXx-x) 证()→(ii)、x2∈L,为〈2,并取>0,使 利〈程+h〈程-h〈x2 据定理3.12,有 (西+)-()<x2)-{2)-2-) 2-为 由了可微,当→0时,对上述不等式取极限后,得到 f')sfa2)-sf'2) 2-为 所以」是1上的递增函数. Gi)→ii)M0,习c1,由微分中值定理和/递增,便可证得 f(x)-f(和)=f"传)x-和)2f'(x和)x-和)
《数学分析》上册教案 第六章 微分中值定理及其应用 海南大学数学系 4 . 令 , 则 , . 显然,上述 L 与 中的点 无关, 故 在 上的每个内闭区间 上满足利普希茨 条件. 由此容易推知 在 上连续,再由 在 上的任意性,又可推知 在 上处处连续. 如果 f 是 I 上的可导函数,则进一步有: 二、凸函数与导数的关系 定理 1(可导函数为凸函数的等价命题) 设 f 为区间 I 上的可导函数,则下述论断互相等价: (1)f 为 I 上的凸函数;(2) f 为 I 上的增函数;(3)对 I 上的任意两点 1 2 x x, 总有 2 1 1 2 1 f x f x f x x x ( ) ( ) ( )( ) + − 证 (i) (ii) ,并取 ,使 据定理 3.12,有 由 可微,当 时,对上述不等式取极限后,得到 . 所以 是 上的递增函数. (ii) (iii) 由微分中值定理和 递增,便可证得

《数学分析》上册教案 第六章微分中值定理及其应用 海南大学数学系 当x〈时,也有相同结论 6i)→()为、2e1,Ae(0,1),并记西-A西+0-)西,则有 -3-(1-(西-2).2-x3-(2-为) 由(iii)可得 [f()2fx)+f'(x3(-x)-=f(x3)+0-0f'(3-x2) f(x2)2f()+f'(3)2-)=f(x3)+'()-为), =(1)+1-0f(x2)2f(x3)=f(x+(1-入)x2) 注定理中m的几何意义如下图所示曲线y冈上任意一点处的切线恒位于曲线的下 方在了为可微的前提条件下,常用上述切线与曲线的位置关系(的来表述凸函数。但是在没有可 微条件假设时,凸函数只能用曲线与其任一弦的位置关系(定义)来定义. y y=f(x) 0 如果f在1上二阶可导,则进一步有: 定理2(凸函数与二阶导数的关系)设f为1上的二阶可导函数,则在I上f为凸(凹)函 数台“>0(<0),x1.f为严格凸一1)"20:2)不在1上的任-子区 间上恒为零 此定理说明:了为严格凸,则曲线中不含有直线段(厂")=0).对于凹函数情形,也有类似 的定理(因为了凸,则了凹). 可导函数∫有如下相互等价的论断: 1)∫为1上四函数. f(x)-f(x)f(x)-fx) 2),西西∈1,<<有名- 一.即割线斜率递减
《数学分析》上册教案 第六章 微分中值定理及其应用 海南大学数学系 5 当 时,也有相同结论. (iii) (i) ,并记 ,则有 , 由(iii)可得 . 注 定理中(iii)的几何意义如下图所示:曲线 上任意一点处的切线恒位于曲线的下 方在 为可微的前提条件下,常用上述切线与曲线的位置关系(iii)来表述凸函数.但是在没有可 微条件假设时,凸函数只能用曲线与其任一弦的位置关系(定义 1)来定义. 如果 f 在 I 上二阶可导,则进一步有: 定理 2(凸函数与二阶导数的关系) 设 f 为 I 上的二阶可导函数,则在 I 上 f 为凸(凹)函 数 f x ( ) 0 ( f x ( ) 0 ), x I . f 为严格凸 1) f x ( ) 0 ;2) f x ( ) 不在 I 上的任一子区 间上恒为零. 此定理说明: f 为严格凸,则曲线中不含有直线段( f x ( ) 0 = ).对于凹函数情形,也有类似 的定理(因为 f 凸,则− f 凹). 可导函数 f 有如下相互等价的论断: 1) f 为 I 上凹函数. 2) 1 2 3 x x x I , , , 1 2 3 x x x 有 2 1 3 2 2 1 3 2 f x f x ( ) ( ) f x f x ( ) ( ) x x x x − − − − .即割线斜率递减

《数学分析》上册教案 第六章微分中值定理及其应用 海南大学数学系 3)(为1上递减函数. 4),∈I,有≤化)+f-),xe1.当f在1上二阶可导时,下述论断与 1),2),3),4)相等价. 5)在1上∫"(x)≤0 对严格凹的情形可类似得出等价论断. 二、拐点 定义2设曲线y=fx)在点(x,f(x)处有穿过曲线的切线,且在切点近旁,曲线在切线的两 侧分别是严格凸或严格凹的,这时称(,f(x)为曲线y=x)的拐点.(即为曲线凹凸部分的分界 点) 必须指出:若(x,fx)是曲线y寸(x)的一个拐点,y=x)在点的导数不一定存在,如 y=派在x=0的情形 定理3(拐点必要条件)若f在x二阶可导,则(x,∫x)为曲线y=x)的拐点的必要条件 是f"(x)=0. 综上知:(x,fx)的拐点,则要么(1)∫“(x)=0:要么(2)f在点不可导. 定理4设f在点x可导,在某邻域U(x)内二阶可导,若在U(x)和U.(x)上f()的符号相 反,则(x,fx)为曲线y=fx)的拐点 例1讨论函数fx)=arctan的凸性与拐,点. 2x 解)=0+,因面当0时.20,当20时.了e0,从而西数了为 (0,0上的凸函数,在0,+o)上为凹函数.而/)在原点连续,故原点为曲线y=)的拐点 例2若f在a,创内可导、凸(凹)函数,则∈a)为f的极小(大)值点台f)=0 即为∫的稳定点 证户)费马定理. =)因∫凸,故xe(a,)有f≥f,)+fx-),因f)=0,故xe(a,)总有 fx)≥f().即为的极小值点. 6
《数学分析》上册教案 第六章 微分中值定理及其应用 海南大学数学系 6 3) f x ( ) 为 I 上递减函数. 4) 0 x I ,有 0 0 0 f x f x f x x x ( ) ( ) ( )( ) + − , x I .当 f 在 I 上二阶可导时,下述论断与 1),2),3),4)相等价. 5)在 I 上 f x ( ) 0 . 对严格凹的情形可类似得出等价论断. 二、拐点 定义 2 设曲线 y=f(x)在点( 0 0 x f x , ( ) )处有穿过曲线的切线,且在切点近旁,曲线在切线的两 侧分别是严格凸或严格凹的,这时称( 0 0 x f x , ( ) )为曲线 y=f(x)的拐点.(即为曲线凹凸部分的分界 点) 必须指出;若( 0 0 x f x , ( ) )是曲线 y=f(x)的一个拐点,y=f(x)在点 0 x 的导数不一定存在,如 3 y x = 在 x=0 的情形. 定理 3(拐点必要条件) 若 f 在 0 x 二阶可导,则( 0 0 x f x , ( ) )为曲线 y=f(x)的拐点的必要条件 是 0 f x ( ) 0 = . 综上知:( 0 0 x f x , ( ) )的拐点,则要么(1) 0 f x ( ) 0 = ;要么(2)f 在 0 x 点不可导. 定理 4 设f 在点 0 x 可导,在某邻域 0 U x( ) 内二阶可导,若在 0 U x( ) + 和 0 U x( ) − 上 f x ( ) 的符号相 反,则( 0 0 x f x , ( ) )为曲线 y=f(x)的拐点. 例 1 讨论函数 f x x ( ) arctan = 的凸性与拐点. 解 2 2 2 ( ) (1 ) x f x x = − + ,因而当 x 0 时, f x ( ) 0 ;当 x 0 时, f x ( ) 0 ,从而函数 f 为 ( ,0] − 上的凸函数,在 [0, ) + 上为凹函数.而 f x( ) 在原点连续,故原点为曲线 y f x = ( ) 的拐点 例 2 若 f 在 ( , ) a b 内可导、凸(凹)函数,则 0 x a b ( , ) 为 f 的极小(大)值点 0 f x ( ) 0 = . 即 0 x 为 f 的稳定点. 证 )费马定理. )因 f 凸,故 x a b ( , ) 有 0 0 0 f x f x f x x x ( ) ( ) ( )( ) + − .因 0 f x ( ) 0 = ,故 x a b ( , ) 总有 0 f x f x ( ) ( ) .即 0 x 为 f 的极小值点

《数学分析》上册教案 第六章微分中值定理及其应用 海南大学数学系 例3设∫在开区间/上为凸(凹)函数,证明∫在开区间1内任一点都存在左、右导数 证只证凸函数在存在右导数,其它情形同理可证。 令00) 则有Fh)≤F)即F为单调递增函数取∈I且≤无,则 f(xo)-f(x)f(xo+h)-f(%o) X0-x4 h 从而F递增有下界,从而mF存在,即,)存在 注对区间端点,左、右导数可能存在,也可能为∞,由第五章1习题10知(若∫在的左、 右导数都存在,则∫在连续),若∫在为开区间a,)内的凸(凹)函数,则f为(a,b)内的连续 函数.(但不一定可导,如f)x) 三、詹森Jensen)不等式 定理(詹森0 Jensen)不等式)设∫为a,1上的凸函数,∈a,b,>0G=l2,川且 乞1则有 f位x)s∑A) (6) 成立.若/为严格凸函数,=1,2,“,川不全相等,则上式严格不等式成立
《数学分析》上册教案 第六章 微分中值定理及其应用 海南大学数学系 7 例 3 设 f 在开区间 I 上为凸(凹)函数,证明 f 在开区间 I 内任一点 0 x 都存在左、右导数. 证 只证凸函数 f 在 0 x 存在右导数,其它情形同理可证. 令 1 2 0 h h ,记 1 0 1 x x h = + , 2 0 2 x x h = + ,则 0 1 2 x x x (取 2 | | h 充分小使 0 2 x h I + ), 由 (3 ) 式得: 0 1 0 0 2 0 1 2 f x h f x f x h f x ( ) ( ) ( ) ( ) h h + − + − 记 0 0 ( ) ( ) ( ) f x h f x F h h + − = ( 0) h 则有 2 1 F h F h ( ) ( ) 即 F h( ) 为单调递增函数.取 4 x I 且 4 0 x x ,则 0 4 0 0 0 4 f x f x f x h f x ( ) ( ) ( ) ( ) x x h − + − − , 从而 F h( ) 递增有下界,从而 0 lim ( ) h F h → + 存在,即 0 f x( ) + 存在. 注 对区间端点,左、右导数可能存在,也可能为 .由第五章§1 习题 10 知(若 f 在 0 x 的左、 右导数都存在,则 f 在 0 x 连续),若 f 在为开区间 ( , ) a b 内的凸(凹)函数,则 f 为 ( , ) a b 内的连续 函数.(但不一定可导,如 f x x ( ) | | = ) 三、 詹森(Jensen)不等式 定理 (詹森(Jensen)不等式) 设 f 为 [ , ] a b 上的凸函数, [ , ] i x a b , 0 i ( 1, 2, , ) i n = 且 1 1 n i i = = ,则有 1 1 ( ) ( ) n n i i i i i i f x f x = = (6) 成立.若 f 为严格凸函数, ( 1,2, , ) i x i n = 不全相等,则上式严格不等式成立

《数学分析》上册教案 第六章微分中值定理及其应用 海南大学数学系 证用归纳法:n=2时命题由凸函数定义显然成立.假设n=k时命题成立,即 4>00-12.23=1 新②o空心要时之40n苦- =空+4=-2经+l (由白销法可.当空,a时空a 卡2=1 因为台1-,故 4x 台1-1∈(a,b)) s0-空-0rs0-2-4 =艺Af)→结论成立 注由于(6)式中当双=2时即为凸函数的定义式(1),所以詹森不等式(6)也可用来作为凸函数 的定义,而詹森不等式的应用也就是凸函数的应用. 对具体的函数套用Jensen不等式的结果,可以证明一些较复杂的不等式。这种证明不等式 的方法称为Jensen不等式法或凸函数法.具体应用时,往往还用到所选函数的严格单调性. 创4证明:对医yeR有不等式兰sg+e 例5设>0G=l2.,川,则 工≤+有当 n 当且仅当所有,全相等时等号成立. 证所有全相等时,等号显然成立.只须证不全等时,有严格不等号成立即可
《数学分析》上册教案 第六章 微分中值定理及其应用 海南大学数学系 8 证 用归纳法: n = 2 时命题由凸函数定义显然成立.假设 n k = 时命题成立,即 0 i ( 1, 2, , ) i k = , 1 1 k i i = = , 则有 1 1 ( ) ( ) k k i i i i i i f x f x = = . 要证 n k = +1 时命题成立.设 0 i ( 1,2, , , 1) i k k = + , 1 1 1 k i i + = = 1 1 1 1 1 1 1 1 1 1 ( ) ( ) [(1 ) ] 1 k k k i i i i i i k k k k k i i i k x f x f x x f x + + + + + + = = = + = + = − + − (由归纳法可知,当 1 1 n i i = = , ( , ) i x a b 时 1 n i i i x = ( , ) a b , 因为 1 1 1 k i i k = = − ,故 1 1 1 k i i i k x = − + ( , ) a b ) 1 1 1 1 1 (1 ) ( ) ( ) 1 k i k i k k i k f x f x + + + = + − + − 1 1 1 1 1 (1 ) ( ) ( ) 1 k i k i k k i k f x f x + + + = + − + − 1 1 ( ) k i i i f x + = = 结论成立. 注 由于(6)式中当 时即为凸函数的定义式(1),所以詹森不等式(6)也可用来作为凸函数 的定义,而詹森不等式的应用也就是凸函数的应用. 对具体的函数套用 Jensen 不等式的结果, 可以证明一些较复杂的不等式. 这种证明不等式 的方法称为 Jensen 不等式法或凸函数法. 具体应用时, 往往还用到所选函数的严格单调性. 例 4 证明: 对 x, y R, 有不等式 ( ) 2 1 2 x y x y e e + e + . 例 5 设 0 i x ( 1, 2, , ) i n = ,则 1 2 1 2 1 2 1 1 1 n n n n n x x x x x x n x x x + + + + + + 当且仅当所有 i x 全相等时等号成立. 证 所有 i x 全相等时,等号显然成立.只须证 i x 不全等时,有严格不等号成立即可

《数学分析》上册教案 第六章微分中值定理及其应用 海南大学数学系 取fx)=-nx,则f在(0,+o)上严格凸,由例4知 -n+++n丙式 即 n 因lhx严格增,故有 +5++x>.X n 1 又x不全等→不全等,故 所以 琴喻 例6在AABC中,求证smA+smB+smC≤3 解考虑函数fx)=sinx,0≤x≤π.”=-sinx<0,0<xπ.→snx在 区间(0,π)内凹,由Jensen不等式,有 .n10:“g=号=号 3 3 snA +snB +sincs 2 例7己知a,b,ceR*,a+b+c=1.求证 /3a+7+/3b+7+/3c+7≤6 解考虑函数fx)=F,f(x)在(0,+o)内严格上凸.由Jensen不等式,有 V3a+7+/3b+7+3c+7_f3a+7)+f(3b+7)+f(3c+)s 3 3
《数学分析》上册教案 第六章 微分中值定理及其应用 海南大学数学系 9 取 f x x ( ) ln = − ,则 f 在 (0, ) + 上严格凸,由例 4 知 1 2 1 1 2 1 1 ln ( ln ) ln( ) n n i n i x x x x x x x n n − = + + + − − = − 即 1 2 1 2 ln ln n n n x x x x x x n + + + 因 ln x 严格增,故有 1 2 1 2 n n n x x x x x x n + + + 又 i x 不全等 1 i x 不全等,故 1 1 1 2 1 1 1 1 ln ( ln ) ln n n i i n i i n x n n x x x x = = − − = − 所以 1 2 1 1 n n n i i n x x x = x 例 6 在⊿ ABC 中, 求证 2 3 3 sin A + sin B + sin C . 解 考虑函数 f (x) = sin x, 0 x . f = −sin x 0 , 0 x . sin x 在 区间 ( 0 , ) 内凹, 由 Jensen 不等式, 有 2 3 3 sin 3 3 ( ) ( ) ( ) 3 sinA sinB sinC = = + + + + = + + A B C f f A f B f C . 2 3 3 sinA + sinB + sinC . 例 7 已知 , , , + + =1 + a b c R a b c . 求证 3 7 3 7 3 7 6 3 3 3 a + + b + + c + . 解 考虑函数 3 f (x) = x , f (x) 在 ( 0 , + ) 内严格上凸. 由 Jensen 不等式, 有 + + + + + = + + + + + 3 (3 7) (3 7) (3 7) 3 3 7 3 7 3 7 3 3 3 a b c f a f b f c

《数学分析》上册教案 第六章微分中值定理及其应用 海南大学数学系 53知+7+36+7+3c+7)-fa+h+c+7)=f8==2.三 3 V3a+7+V3b+7+3c+7≤6. 例8已知a>0,B>0,a2+B≤2.求证a+B≤2.(留为作业) (解函数f(x)=x在(0,+o)内严格下凸.由Jensen不等式,有 am〔e-@g.2号1- 2 2 (a+B3≤8,→a+B≤2.) 作业P15333),5,81):P158-15917,18,19
《数学分析》上册教案 第六章 微分中值定理及其应用 海南大学数学系 10 ( 7) (8) 8 2 3 3 7 3 7 3 7 3 = + + + = = = + + + + + f a b c f a b c f . 3 7 3 7 3 7 6 3 3 3 a + + b + + c + . 例 8 已知 0 , 0 , 2. 3 3 + 求证 + 2 . ( 留为作业 ) ( 解 函数 3 f (x) = x 在 ( 0 , + ) 内严格下凸. 由 Jensen 不等式, 有 = + + = + = + 2 ( ) ( ) 8 2 2 ( ) 3 3 f f f = + 1, 2 2 2 3 3 ( ) 8, 2 3 + + . ) 作业 P153 3⑶,5,8⑴; P158—159 17,18,19